
文章图片
文章图片
文章图片
文章图片

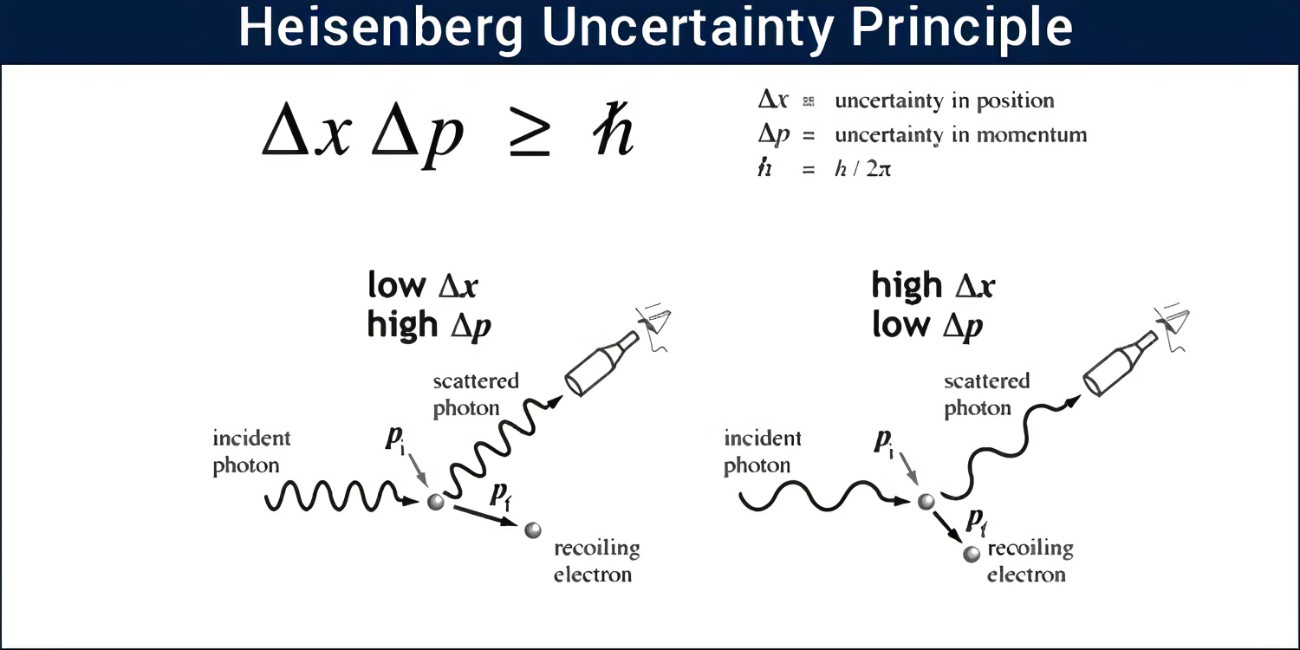
量子天文学:海森堡不确定性原理
这是四篇文章系列中的第二篇文章 , 每篇文章都单独解释不同的量子现象 。 每一篇文章都是镶嵌画中的一块 , 所以需要每个人都理解我们提出的量子天文学实验的最终解释 , 这可能是使用艾伦阵列望远镜和由SETI研究所和加利福尼亚大学伯克利建立的窄带电波探测器得出的 。
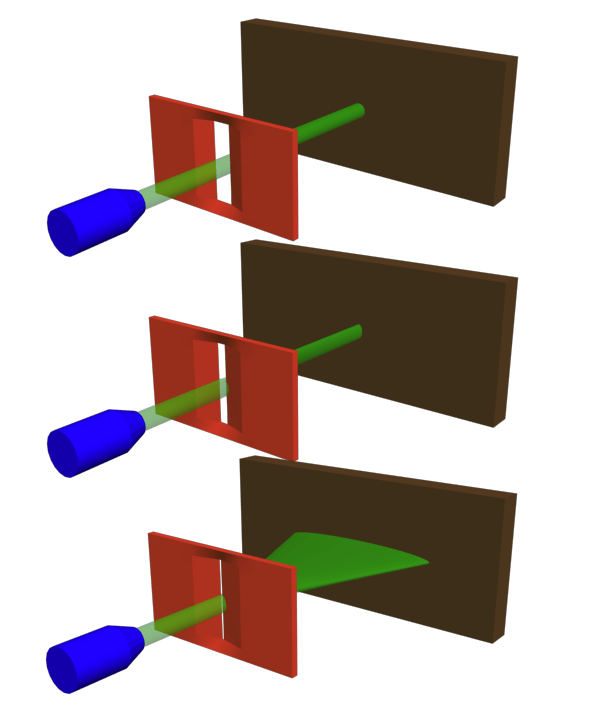
在第一篇文章中 , 我们讨论了双缝实验 , 以及如何将光量子粒子(光子)想象为概率波 , 直到这种概率波被实际检测到 。 在这篇文章中 , 我们将研究量子物理学的另一个特点 , 即对实际可测量的东西施加基本限制 , 这是沃纳·海森堡首次发现的一个基本性质 , 其最简单的形式被称为“海森堡不确定性原理” 。
在科学界 , 我们可能习惯于将“原理”一词视为“秩序”、“确定无疑的事”或“宇宙法则” 。 因此 , “不确定性原理”一词在我们看来可能类似于“巨型虾”或“客座主人” , 即矛盾 。 然而 , 不确定性原理是量子物理的一个基本性质 , 它最初是通过某种经典理论发现的 , 是一种基于经典的逻辑 , 今天许多物理教师仍在使用它来解释不确定性原理 。 这种经典理论是 , 如果一个人用光来观察一个基本粒子 , 用光(即使只有一个光子)来撞击这个粒子 , 就会观察到它被撞偏 , 这样一个人就不能再分辨出这个粒子的实际位置 , 即只知道它已经不在原来的位置了 。
波长较短的光(例如 , 蓝光 , 能量较大)比波长较长的光(例如 , 红光 , 能量较小)向粒子传递更多的能量 。 因此 , 使用波长较短(更精确)的光“尺度”来测量位置意味着 , 通过用更多的能量“撞击”粒子 , 可以使粒子的可能位置更“混乱” 。 沃纳·海森堡在他的支持者内尔斯·波尔(成功地与爱因斯坦就许多问题进行了辩论)旅行时 , 首次发表了他的不确定性原理论文 , 或多或少使用了上述的经典理论 。 (与经典概念不同的是 , 光是以小包或小量的形式出现的 , 如第一篇文章所讨论的 , 称为“量子”) 。 然而 , 事实证明 , 不确定性原理比海森堡在他的第一篇论文中想象的更为基本 。
动量是物理学中的一个基本概念 。 它的经典定义是粒子的质量乘以其速度 。 我们可以想象以每小时100英里的速度朝我们投掷一个棒球 , 其效果类似于以每小时10英里的速度朝我们投掷球棒;虽然它们的质量不同 , 但它们的动量大致相同 。 海森堡不确定性原理基本说明 , 如果人们开始很好地了解基本粒子动量的变化(通常是粒子速度的变化) , 那么人们就开始不知道粒子位置的变化 , 也就是粒子的实际位置 。 另一种表述这一原理的方式是 , 在公式中使用相对论 , 结果是 , 我们得到了不确定性原理的另一种形式 。 该相对论形式描述 , 当我们很好地了解一个基本粒子的能量时 , 我们不能同时非常准确地知道(即测量)它实际上在什么时候有该能量 。 所以在量子物理学中 , 我们有所谓的“互补对”(如果你真的想给你的朋友留下深刻印象 , 你也可以称他们为“不对易的可观测量” 。 )
人们可以用一个没有完全充满的气球来说明不确定性原理的基本结论 。 一方面 , 我们可以写“的delta-E”来表示粒子能量值的不确定性 , 另一方面 , 我们可以写“delta-t” , 代表粒子拥有能量的时刻的不确定性 。 如果我们挤压delta-E侧(例如 , 限制能量使其适合我们的手) , 我们可以看到气球的delta-t侧会变大 。 类似地 , 如果我们决定让delta-t侧适合我们的手 , delta-E侧会变大 。 但气球中空气的总值不会改变;它只会转移 。 在我们的类比中 , 气球中空气的总值是一个量 , 或一个“量子” , 即量子物理学中可能的最小能量单位 。
【不确定性原理,是人为测不准,还是真的不确定?】
推荐阅读
- 视网膜色素变性怎么知道自己有没有被遗传?基因检测去哪里做
- 经典案例:一桩15岁少年畸恋35岁美女教师引发的荒唐血案
- 爱因斯坦的百年难题:若世上剩你一人,有敲门声,你会开门吗?
- 是谁在背后操纵着宇宙的一切?或许爱因斯坦的猜测是正确的
- 人类进化史也是一部灭绝史:北京猿人惨遭屠杀,还被当成食物
- 光的速度高达30万公里/秒,它前进的动力是什么?
- 外星人为什么无法入侵地球?爱因斯坦曾预言神秘能量在保护人类
- 时间是否真的存在?是否只是我们对过去现在未来的一种衡量尺度?
- 如果发生第三次世界大战,世界会变成什么样子?爱因斯坦给出答案







