
文章图片
图源南开大学
演讲 | 陈省身
今天我很荣幸能有这个机会同大家讲话 。 我先讲两个故事 。
我们都知道欧几里得(Euclid)的《几何原本》 , 这是一本数学方面的论著 。 完成于2000多年以前 。 它对于人类是一个很伟大的贡献 。 书中包括了分析和代数 , 不限于几何 , 目的是用推理的方法得到几何的结论 。
其中 , 第13章的内容讲的是正多面体的面数 。 正多面体就是这样一个多面体:它的面互相重合 , 同时通过一个顶点和每面的边数是相同的 。 正多面体在平面上的情形是正多边形 。 正多边形很多 , 有正三角形、正四边形……等等 。
当时发现 , 到了空间 , 讨论正多面体就不这么简单了 。 空间的正多面体少得多 , 一共有五种正多面体:四面体、六面体、八面体、十二面体 , 最大的一个是正二十面体 。 有个朋友写了一本书 , 把这些漂亮的几何图形都收进去了 , 我这里有一份彩色的拷贝 。
有些人可能会想 , 数学家们一天到晚没有事情可做 , 无中生有 , 搞这些多面体有什么意思?不过我跟张存浩先生讲 , 现在化学里的钛化合物就跟正多面体有关系 。 这就是说 , 经过2000年之后 , 正多面体居然会在化学里有用 , 有些数学家正在研究正多体和分子结构间的关系 。 我们也知道 , 生物学上的病毒(Virus)也具有正多面体的形状 。 这表明 , 当年数学家的一种“空想” , 经历了这么长的时间之后 , 竟然是很“实用”的 。
我再讲一个许多人都在讲的故事 。 有两个中学时代的朋友 , 多年未见了 , 一天忽然碰到 。 甲对乙说:“你这些年在做什么事?”乙说:“我在研究人口问题” 。 甲当然很想看看老朋友的工作 , 于是拿来乙的人口学论文一读 , 发现论文出现很多π 。 他觉得好奇怪:π是圆周率 , 圆周与直径之比 , 这怎么会和人口扯上关系?这个问题与上面的正多面体问题说明了同样的一点 , 即基础科学 , 特别是纯粹数学很难说将来会在什么时候会有用 , 并且起到很重要的作用 。 如果要求基础科学立刻就要有应用 , 那是太短视了 。
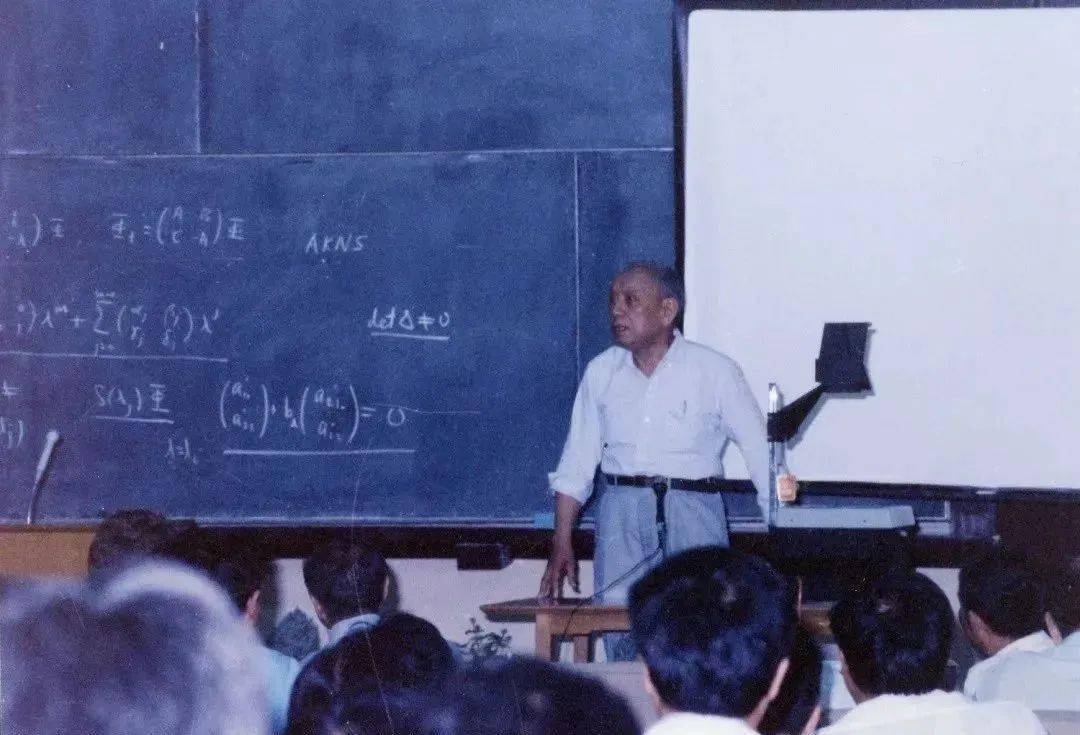
文章图片
图源:南开大学
数学家经常在家里思想问题 , 想出来的东西为什么会有用?我想 , 主要的原因就是它的基础非常简单 , 又十分坚固 , 它的结果是根据逻辑推理得出来的 , 所以完全可靠 。 逻辑推理比实验证实所获的结果要更为可靠些 。 数学由于它的逻辑可靠性 , 因而是一门有坚实根底的学问 , 这是数学有用的一种解释 。
推荐阅读
- 21世纪经济报道|电商“失速” 代运营机构谋变
- 21世纪经济报道|中国5G连接数已近4.3亿 加速探索垂直应用市场
- 思考|七宝德怀特“男神”教师:21世纪,千万别缺少这种底层思维
- 难题|全力突破21世纪最大数学难题,新入职华为数学家有多牛?
- 21世纪经济报道|南财快评:互联网“拆墙”是一个正和博弈
- 21世纪经济报道|被马斯克抛售后,特斯拉股价暴跌13%后企稳,背后有何隐情?
- 21世纪经济报道|元宇宙大爆炸:泡沫还是风口?
- 21世纪经济报道|奔跑的“剧本杀” 行业乱象频现
- 21世纪经济报道|俞敏洪高调带货 新东方却在悄悄创新
- 21世纪经济报道|抖音腾讯终于要开放了!







