世界上只有5种正多面体的另一种证明方法
文章图片
文章图片
【世界上只有5种正多面体的另一种证明方法】
文章图片
文章图片
什么叫做球面上均布孔呢?
做机械工程的人 , 经常遇到在一个圆面上圆周阵列孔的问题 。 在圆面一个圆周上阵列孔的数量 , 最少为2个 , 最多有无穷多个 。 如果在球面上圆周阵列孔 , 它的数量又是多少呢?
经过我的研究 , 我发现在球面上圆周阵列孔的数量 , 只有5种情况 , 分别为4个 , 8个 , 20个 , 6个 , 12个 。 正好与5种正多面体的顶点数量完全一致 。
为了明确球面上均布孔的概念 , 需要满足以下几个要求 。
1.孔的类型和大小都是相同的 , 孔的基准轴都指向球心并且过球心 。
2.所有孔的基准轴与球面的交点 , 都位于球面上 , 但不能都位于过球心的一个平面上 。
3. 以任意一个孔的基准轴为阵列轴 , 周围最小距离相邻的孔在圆周上均布且数量相等 。 对于所有孔 , 最小距离都是相同的 。
什么叫做均分球面呢?
将球面上均布的孔 , 改成点 , 然后将所有最小距离相邻的点用直线连接起来 , 得到球的内接正多面体 , 用所有过球心和正多面体棱的平面去分割球面 , 就能将球面分割成形状和大小完全相同的曲面实体 , 这就叫做均分球面 。
同样的道理 , 均分球面的数量 , 只有5种情况 , 分别为4个 , 6个 , 12个 , 8个 , 20个 。 正好与5种正多面体的面数量完全一致 。 将所有最小距离相邻的点用直线连接起来 , 得到球的内接正多面体 , 只有5种 , 分别是正四面体 , 正六面体 , 正二十面体 , 正八面体和正十二面体 。
只有五种正多面体的solidworks软件证明
证明如下:5种正多面体 , 可由均分球面得到 , 因此问题转化为均分球面一共有多少种情况 。 点可以理解为孔的最小极限 , 均布点可看作均布孔的特殊情况 。 按照球面上均布孔的三个要求 , 我们开始用solidworks软件来作草图 。
1、m=2 , 不可能 。
在前视基准面上画草图 , 画一个任意大小的圆 , 给该圆添加固定约束 。 我们总能找到一个均分点 , 让它位于圆最上面的象限点上 。
以该均分点与球心的连线作为阵列轴 , 在位于球面上的水平圆周上 , 如果只阵列两个点 , 将其中一个点转到草图圆上 , 根据圆周上两点阵列的特点 , 则另一点一定也位于草图圆上 。 根据均布孔要求3 , 分别以另外两点与球心的连线作为阵列轴 , 阵列周围最小距离相邻的点 , 得到的点 , 显然也都是位于草图圆上 。 同样的道理 , 阵列得到的所有点 , 也都会位于草图圆周上 , 即所有点都位于过球心的前视基准面上 。 不能满足均布孔要求2 , 因此只阵列两个点 , 不能均分球面 。 排除 。
2、m=3 , n=3 , 有解 。
接上面 , 如果只阵列三个点 , 将其中一个点转到草图圆上 , 根据圆周上三点阵列的特点 , 则另两点一定不位于草图圆上 。
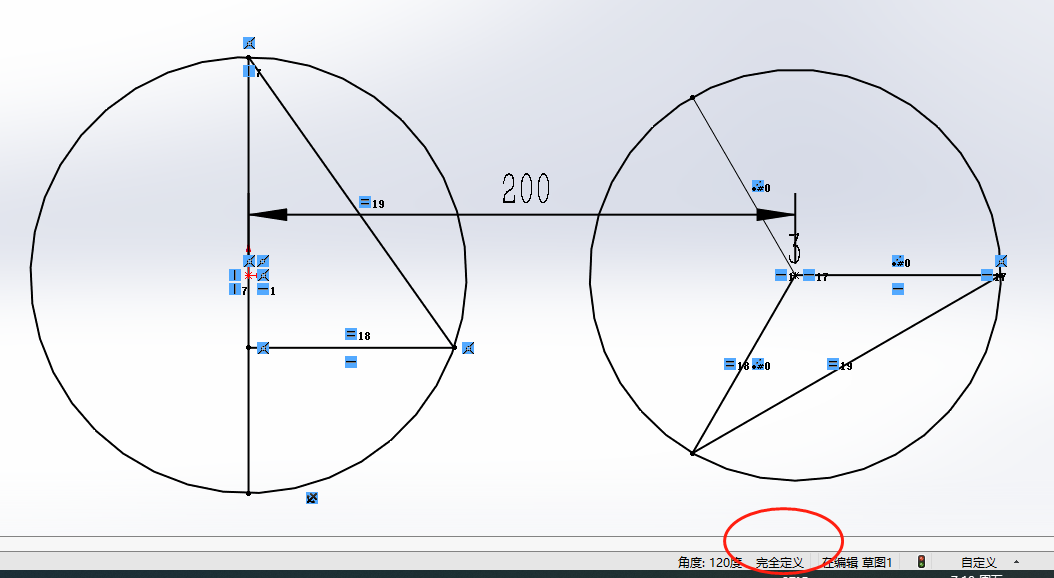
将球面上的水平圆周上的三点 , 在旁边画一个草图 , 这里的圆称为副圆 , 左边的圆称为主圆 , 根据均布孔的要求 , 可以让副圆上阵列相邻点的距离等于主圆最上面象限点与阵列点之间的距离 。 如下图所示:
草图是完全定义的 , 说明草图有唯一确定的解 。
按照以上思路继续画下去 , 能够画出整个球面上的均分点 , 均分点的数量是4个 。 说明m=3 , n=3 , 有解 。
3、m=3 , n=4 , 有解 。
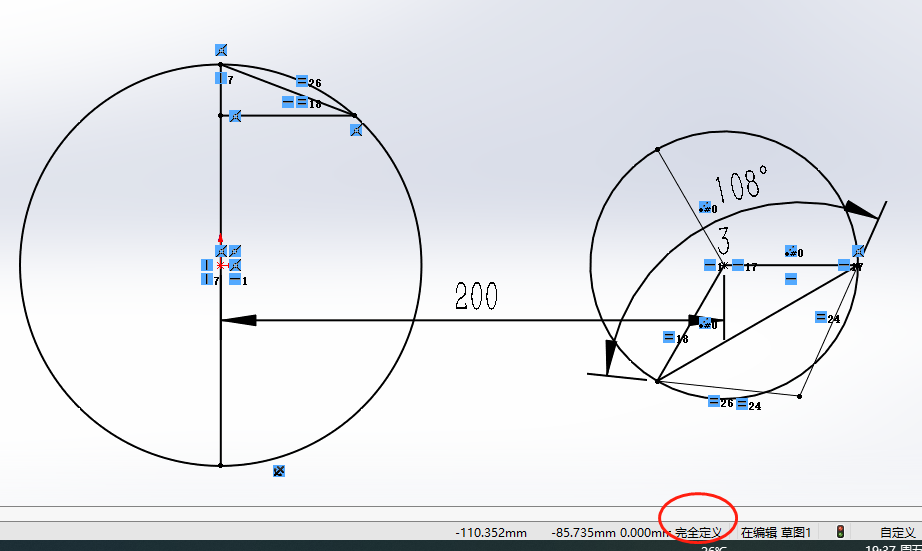
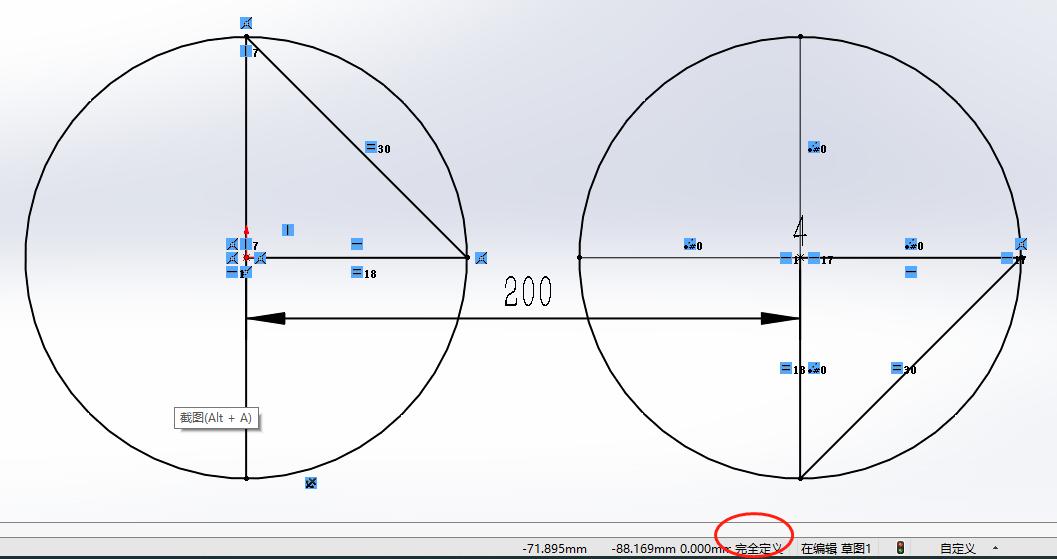
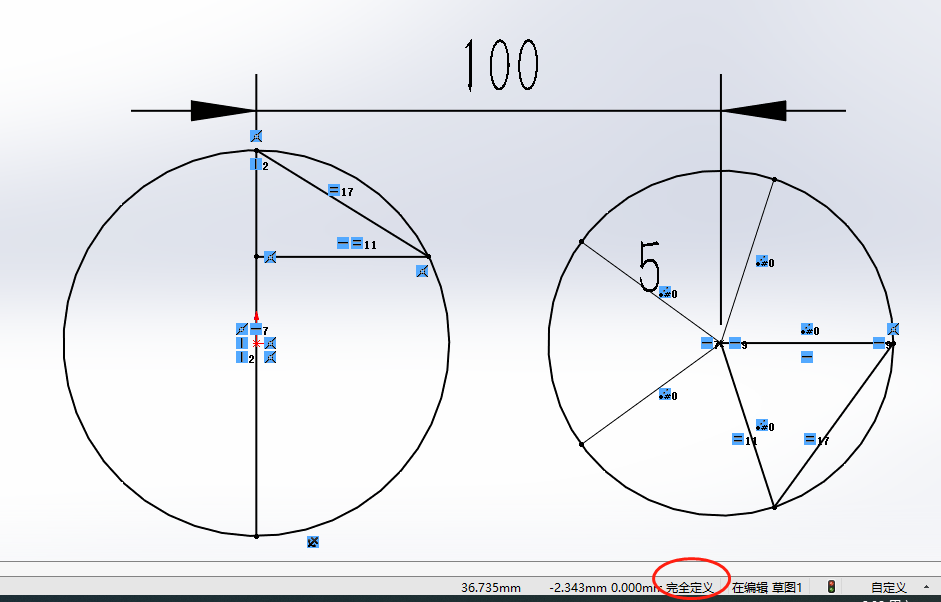
接上面 , 可以让副圆上阵列相邻点的距离大于主圆最上面象限点与阵列点之间的距离 , 假如过主圆最上面象限点和副圆上相邻两点的平面上 , 存在第四个点 , 那么该平面内的4点 , 按照最小距离连接起来 , 是一个正方形或者菱形 。 过球心向四边形作垂线 , 垂足设为O点 , 可求证得到O点到四边形各顶点的距离相等 , 因此四边形不可能是菱形 , 而是正方形 。 正方形对角线长度等于边长的√2倍 。 如下图所示:
推荐阅读
- 世界上有一种鸟,尾巴长得像丝带,你知道是哪种鸟吗?
- 世界上最长寿的生物,竟然真能达到理论上的永生
- 世界上最大的天鹅近亲,体形和大猫有7-10厘米之间的差距
- 科学家发现宇宙最强爆炸,原因只有1种,超出质能方程上限,可横扫生命毁灭文明
- 全身DNA断裂会发生什么?全球只有一个人不幸遇到,结果很心痛
- 56岁阿姨相亲62岁大爷很满意,只有一个要求,大爷:我没问题
- 作为世界上最大的猛禽,它的一双翅膀翼展可达3.3米,然而却不会捕猎?
- 盘点世界上最丑的十种动物,丑到极致是惊艳,你见过几个?
- 世界上最大的生物是什么?180吨重的蓝鲸根本排不上号!
- “大男子主义”的查尔斯:求婚几次都被拒绝,只有卡米拉忍他50年







