初二|初二数学下册:平行四边形判定5大常用方法?
平行四边形的判定方法主要有:
(1)两组对边分别平行;
(2)两组对边分别相等;
(3)一组对边平行且相等;
(4)对角线互相平分;
(5)两组对角分别相等 。
平行四边形的上述判定方法 , 分别从边、对角线、角三个角度 , 给出了确定一个四边形是平行四边形的根据 。
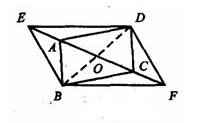
如图 , 点E、F为平行四边形ABCD的对角线AC所在直线上的两点 , 且AE=CF 。 求证:四边形EBFD是平行四边形 。
文章图片
证法1:∵四边形ABCD为平行四边形 ,
∴AB=CD , AB∥CD 。
∴∠BAC=∠DCA 。
∴∠BAE=∠DCF(等角的补角相等) 。
∴△BAE≌△DCF(SAS) 。
∴∠BEA=∠DFC(全等三角形的对应角相等) 。
∴BE∥DF(内错角相等 , 两直线平行) 。
同理可得:DE∥BF 。
∴四边形EBFD是平行四边形(判定方法(1)) 。
证法2:同上证法 , 可得△BAE≌△DCF 。
∴BE=DF 。
同理可得:△DAE≌△BCF(SAS) 。 故DE=BF 。
∴四边形EBFD是平行四边形(判定方法(2)) 。
证法3:同证法1可得△BAE≌△DCF 。
∴BE=DF 。 ∠BEA=∠DFC 。
∴BE∥DF 。
∴四边形EBFD是平行四边形(判定方法(3)) 。
上面的三种方法都借助了△BAE≌△DCF , 只是最后几步出现了差异 。
证法4:如图2 , 连接BD交AC于点O 。
∵四边形ABCD为平行四边形 ,
∴AO=CO , BO=DO 。
又∵AE=CF ,
∴AO+AE=CO+CF , 即OE=OF 。
∴四边形EBFD是平行四边形(判定方法(4)) 。
这种方法能够紧紧抓住条件的整体特征 , 构造出了四边形EBFD的对角线 , 从而证明了四边形是平行四边形 。
证法5:可根据前面证法所得到的△BAE≌△DCF和△DAE≌△BCF , 得到∠EBF=∠FDE , ∠BED=∠DFB 。
∴四边形EBFD是平行四边形(判定方法(5)) 。
这种方法从角的角度证明了所给的四边形是平行四边形 。
上面这些证法中 , 证法3、证法4最简便 。
end
声明:本文内容来源于网络 , 转载请联系原出处 。初三研究中心尊重版权 , 如有侵权问题 , 请及时与管理员联系处理 。
【初二|初二数学下册:平行四边形判定5大常用方法?】点击 "阅读原文" 加 中考君微信好友哦
推荐阅读
- 笔记|初二语文下册:《阿西莫夫短文两篇》课堂笔记整理
- 模型|中考数学图形旋转难?用5个模型就能搞定
- 定义|初一数学下册:平方根知识点
- 逻辑|数学是发明还是发现?(一)
- 初二|初二数学下册:一次函数知识点
- 闫某某|数学论文作者数从平均每篇2.1个增长到了2.4个丨巨变里,你可能没意识到的小事
- nVIDIA|传Hopper GPU继任者代号Blackwell 致敬统计数学家大卫·布莱克威尔
- 华罗庚|华罗庚的数学成就
- 线下|国际数学联盟:谴责俄罗斯行动,国际数学家大会改为全线上
- 平行线|初二数学下册:平行四边形知识点







