易坊好文馆

  1. 首页 > 玩科技 >

逻辑|数学是发明还是发现?（一）

迈克尔·阿蒂亚爵士（Sir Michael Francis Atiyah ， 1929年4月22日~2019年1月11日） ， 英国数学家 ， 毕业于剑桥大学三一学院 ， 前英国皇家学会会长 ， 被誉为20世纪最伟大的数学家之一 。
【逻辑|数学是发明还是发现?（一）】>>>>
迈克尔·阿蒂亚出生于英国伦敦 ， 童年时代在中东地区度过 ， 1945年跟随家人移居英国 ， 之后以前三名的成绩考入剑桥大学三一学院 。 1955年获得博士学位 ， 毕业后在普林斯顿高等研究院、剑桥大学彭布罗克学院、牛津大学等学术机构研究、任教 ， 并在1962年成为英国皇家学会会员 。
迈克尔·阿蒂亚爵士的主要研究领域是几何 ， 而到20世纪70年代他把重心转移到数学物理学上 。 1960年代他与艾沙道尔·辛格建立合作关系 ， 共同证明了阿蒂亚-辛格指标定理 ， 该定理在数学的一些领域均有重要作用 。 因此他在1966年荣获菲尔兹奖 ， 2004年又与艾沙道尔·辛格共同获得阿贝尔奖 。 除此之外 ， 迈克尔·阿蒂亚爵士在拓扑、微分方程、数学物理、代数等领域也有杰出成就 。 1983年 ， 被英国皇室授予下级勋位爵士 。 1992年 ， 获得英国功绩勋章 。
逻辑|数学是发明还是发现?（一）
文章图片

“数学 ， 是发明还是发现?” ， 这是一个相当富哲学性的题目 。 这个题目并非专为数学家而设 ， 而是适合更广泛的读者 。 我们真正关心的 ， 是数学与现实世界及其他事情之间的关系 。
数学可以说是处于艺术和科学之间的学科 ， 而数学和科学的关系 ， 几乎人所共知 。 例如牛顿、麦克斯韦(James Clerk Maxwell)和爱因斯坦所提出的理论 ， 是建基于很坚实的数学基础之上 。 反过来 ， 科学家的观察和理论验证 ， 又对数学的发展产生很大的影响 。 然而 ， 数学与艺术之间的关系 ， 便不是那样显而易见了 。
数学是艺术也是科学
人们认为 ， 艺术和数学是两码子事 ， 其实两者之间是有关联的 。 首先 ， 数学是建基于逻辑——严密的逻辑思维 。 在哲学领域里 ， 同样也十分注重逻辑和思考分析 。 例如 ， 两位在不同年代的伟大哲学家 ， 古希腊的柏拉图和近代的罗素 ， 他们亦为数学家 ， 因为二人的思想都采用大量数学语言 ， 无可置疑 ， 逻辑属于哲学的一部分 。
同时 ， 逻辑也是建构艺术的基础 。
当我们说到某些艺术的项目 ， 如绘画 ， 便会趣用到很多透视的方法 ， 也即是空间里的三维观点;透视圆法 ， 亦被视为绘画艺术发展的一大发现 。 又例如音乐 ， 音乐使用了音符作为基础 ， 但当中的和弦其实是一种十分精确和美妙的数学形式 ， 这也表现出艺术和数学的关系 。 建筑学追求的是建筑物的美 ， 这取决于建筑物本身的比例和规模等;无论是几何学 ， 或几何学建筑 ， 都是建筑学中的十分重要的部分 。
数学与大量艺术项目之间的关系可谓千丝万缕 。 概言之 ， 艺术就是主观的美 。 在物理学 ， 对美的追求 ， 是来源于艺术的基本概念 。 同样 ， 对美的追求 ， 在数学亦是重要的环节;因此可以说 ， 数学既是艺术 ， 也是科学 。
逻辑|数学是发明还是发现?（一）
文章图片

科学和艺术之间的区别 ， 可以这样加以阐释——科学家孜孜不倦去钻研和发现在他眼前的世界 ， 借着科学我们可以发现事物的真相和自然世界的法则 ， 比如科学家发现了高温超导电性 ， 这个发现就是建基于从观察中得出的论据 。 另一方面 ， 艺术则是人类的一种创作 。 人在思考中 ， 获得了重要的发现和感悟 ， 这个发现的基础并非建立在理性思考 ， 而是在感情上 。
表面上 ， 艺术和科学是根本上相逆的东西 ， 但事实并非如此 。
数学模型来自思维概念
让我从人类发展的历史 ， 回溯到数千年前 ， 现实世界和人类之间有什么关联 。 什么是现实世界?它意味着什么?当时的人类是如何思考这个世界?我们不理解现实世界 ， 也不理解思维 ， 更不理解它们之间的关系 。
这是其中一个重要的哲学问题 。 当然 ， 哲学问题并不必然有确切的答案 。 我们能通过提出问题 ， 从中学习获得智慧 ， 但却永不能得到一个确切的答案 。 因此 ， 古今哲学家为了一个哲学问题 ， 而消磨了上千年时间 。 事实上 ， 人类提出科学理论 ， 是把我们所观察到的事物 ， 以一个模型或框架去理解、解释和发展规律 。 这样 ， 在某种程度上 ， 科学理论和数学模型十分类似 。 它们都是人类思维内的概念 ， 我们可将这些概念 ， 加诸在外间所观察的事物 ， 好以理解它们 。
因此 ， 在某程度上 ， 科学有两个部分 ， 包括外间实验的数据 ， 以及人类内在思维所得的数学模型 ， 并尝试把两者融合起来 ， 得到一个整体的认识 。 同样的 ， 艺术也有两个部分 。 一、源于艺术家发自内在感受的创作 ， 二、在外在物理上所受到的约束 。 例如 ， 数学结构和建筑物的透视点都受到来自外在的约束 ， 是艺术家不能置之不理的 。
所以 ， 艺术家应用他们的创作 ， 但也是生活在各种已被发现的“框架”之内 ， 所谓“鱼在水中 ， 水也在鱼中” 。 在某程度上 ， 艺术和科学都分享着同样的特性 ， 就是它们在“发现”这些框架 ， 并在这框架之内进行各种创作 。
这框架是科学所仗赖的数据 ， 或是我们研究能力所及的范围 。 艺术家同样面对框架 ， 但他们尝试把自己的意念形象化 。 理性和感性是科学的基础 ， 也是艺术的基础 ， 但大多数人都认为 ， 二者是河水不犯井水 ， 甚至风马牛不相及 。 然而 ， 从近年有关人脑的研究 ， 我们知悉了一些令人振奋的成果 ， 它显示出人脑中理性和感性 ， 彼此相互影响着“你中有我 ， 我中有你” 。 或许 ， 我们能在将来对这方面知道更多 ， 了解更多 。 所以 ， 数学是艺术也是科学 。
柏拉图世界是早已存在还是创造出来的?
让我们尝试从多种方法去说明这两个方面 。 问题在于 ， 数学家所发现的东西 ， 是存在于现实世界中?还是存在于柏拉图式的理想世界?柏拉图用他构想的概念来理解数学 ， 例如 ， 他认为圆形可以是完美的 。 但完美的圆 ， 在现实世界中从不存在 ， 所有我们所画的圆形 ， 总会带点棱角 。
事实上 ， 完美的圆形只是一种想法 。 我们现在称柏拉图式的世界 ， 确实是一种想法 ， 一个理想世界 。 在现实世界中 ， 我们见到的圆形 ， 只是柏拉图理想世界的一种想法、反映和替代 。 但也有人相信 ， 柏拉图世界确实存在 ， 在那里 ， 所有伟大的数学想法都能完美地、和谐地共存 。 然而 ， 现实世界里竟存在着杂乱 ， 于是科学家便以某些方法 ， 把现实世界和想像世界两者合并 。
接下来 ， 大家也许会问:究竟柏拉图式的世界是否从一开始就存在 ， 只待我们去发现吗?抑或纯粹是人类智慧所创造的?它是一件发明还是一次发现?也就是说 ， 我们发明了柏拉图式的世界 ， 接着 ， 这个理想世界反映了现实世界 。
这是一个已存在了上千年的疑问 。 这正是一条我们可以辩论 ， 却会获得不同答案的问题 。 一般来说 ， 我们从一些基础层面的例子去探讨这些问题 ， 会比进行抽象层面的哲学讨论 ， 会更加有效 。 因此 ， 我将透过一些简单的例子 ， 去讨论这个问题:数学是一种发明 ， 或是发现?
在进一步讨论之前 ， 让我指出一点 。 香港是一个以商业为本的城市 。 许多人们来到大学念书或教书 ， 都难免考虑到金钱和物质的问题 。 从这方面来说 ， 发明和发现之间的一个主要区别 ， 就是透过发明可以获得专利权 ， 从中可以赚取金钱 ， 而发现却不是 。 例如 ， 马克士威引进了电磁学理论 ， 如果他发现的公式可以取得专利 ， 恐怕他已经和微软的盖茨一样富有了 。 但是 ， 你不能为自己所发现的东西取得专利权 。 人类基因组是近期另一个例子 ， 并且引起了许多争论 ， 比如说 ， 我们能否为人类基因的发现而取得专利?因为这个题目涉及庞大的利益 ， 所以经常引起广泛的争论 。 因此 ， 这是一项发明还是发现的问题 ， 不纯然是一个哲学议题 ， 也引起了强烈的商业回响和争论 。
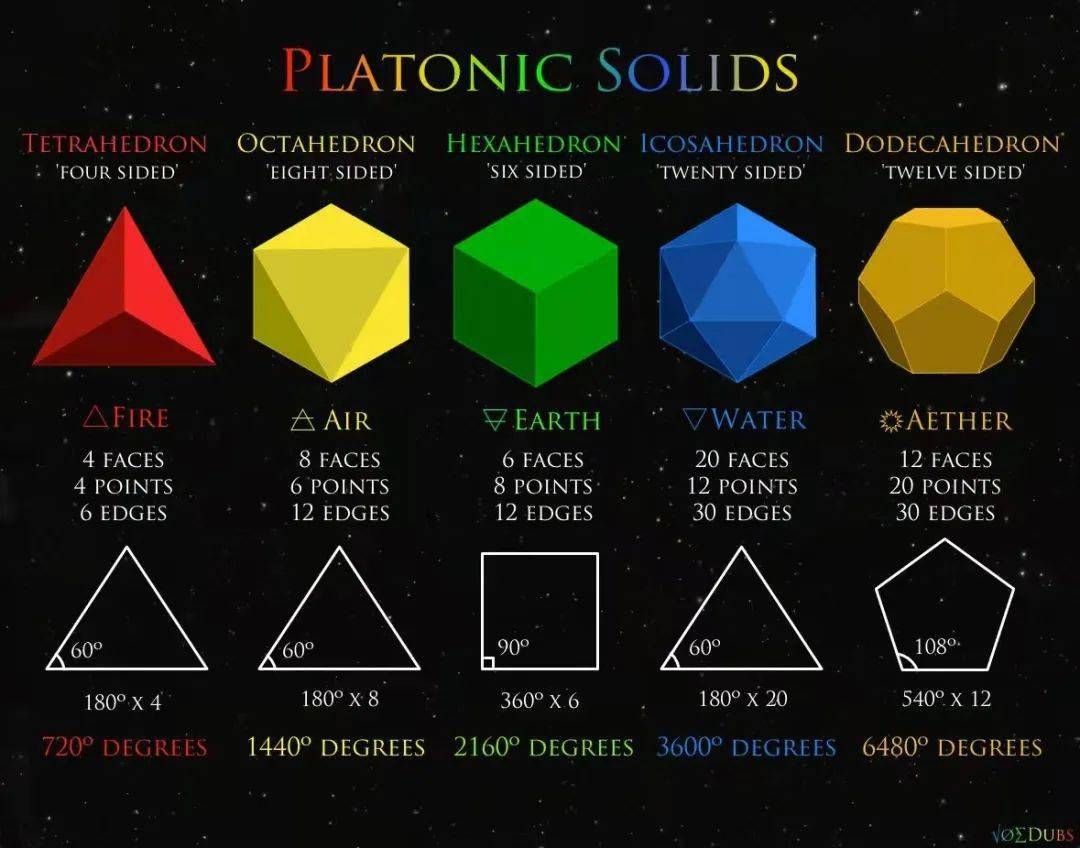
现在 ， 让我先以柏拉图和希腊人的数学概念作为我们讨论的一个例子 。 柏拉图感兴趣的其中一个问题 ， 是著名的“正多面体” ， 也被称为“柏拉图立体” 。 “正多面体”有 5 个:
正四面体 ， 由4 个三角形组成;
正六面体 ， 即正立方体;
正八面体 ， 即一个双金字塔;
正十二面体 ， 每一个面皆是正五边形;
正二十面体 ， 每一个面皆是等边三角形 。
一个正四面体有4个顶点 ， 6 条边和4个面;
正方体有 8 个顶点 ， 12 条边和 6 个 面;
正二十面体 ， 有20 个三角形的表面 ， 12 个顶点 ， 和30条边 。 同时 ， 它们成双出现 ， 就是面的数目和顶点的数目 ， 可以互相交替 ， 称为对偶 。 首要的问题是 ， 像正二十面体或其他立体的这些物体 ， 究竟是被发现还是被发明出来?
逻辑|数学是发明还是发现?（一）
文章图片

你可以争论:立方体是一件明显存在于周围中的东西 ， 就像方糖一样;而四面体或许也是这样 。 但是 ， 于大自然中找到正二十面体却十分困难 。 我不认为它们以任何形式存在 ， 所以 ， 正二十面体看来更加像是一件人类的发明 。 虽然它的存在归功于柏拉图 ， 但我发现事实上在公元前2000年 ， 即4000年前的苏格兰 ， 便存在着正二十面体和所有5个正多边形立体 。 这比柏拉图的年代更早出现 ， 至少比柏拉图早了千年 。 这些可能是文物的石块 ， 出现于苏格兰还没发展出高度文明的一个时代里 ， 而当时已经有人研究出如何做出全部五个立体 。
—版权声明—
来源：好玩的数学 ， 编辑：nhyilin
仅用于学术分享 ， 版权属于原作者 。
若有侵权 ， 请联系微信号:Eternalhui或nhyilin删除或修改！
—THE END—
? 田渊栋：业余做研究的经验
? 颜宁：当科学家是幸福的
? 最简单概率论的五个智慧
? 我国数学前9强王牌院校实力大解析！清华跌出前三甲！
? 量子力学的路径积分和退相干诠释
? 量子力学英雄谱

    推荐阅读


    上一篇：雷锋|让雷锋精神在中华大地持续闪耀

    下一篇：Samsung|又一数码巨头成受害者 三星遭NVIDIA同一组黑客攻击