
文章图片
文章图片
文章图片

文章图片
月球是地球唯一的卫星 , 不但对于保护地球少受地外小行星的撞击起到了重要的作用 , 同时也是人类进行深空探测最理想的“基地”和“跳板” 。 随着我们科学技术的飞速发展 , 相信用不了多久 , 到月球上旅行会成为“家常便饭” , 而在月球上观察地球以及太阳系内的其他近距离行星 , 估计也会另有一番风情 。 由于月球上几乎没有大气层 , 那么来自外太空恒星直接照射或者行星反射的光线 , 势必在几乎没有什么损耗的情况下到达月球表面 。 假如在月球上我们看到了地球的近邻之一火星 , 用枪瞄准它开一枪 , 能否打到火星上面去呢?
在17世纪末 , 伟大的物理学家牛顿发现了万有引力定律 , 认为宇宙间无论是宏大的星体 , 还是微观粒子之间 , 都存在着相互吸引的能力 , 这种能力是本身所固有的 , 所有称之为“万有”引力 。 这个引力的数值 , 与相互产生这种作用力物体的质量乘积成正比 , 与它们之间的距离平方成反比 。 如果两个相对静止的物体 , 在排除其它作用力时 , 万有引力的存在使得它们会有相互靠近的趋势 , 并最终碰撞到一起 。 然而 , 在宇宙空间中 , 绝大部分的星体的运动都自有一套规律 , 那就是公转和自转 。 对于公转来说 , 那就是围绕着一个起到绝对性作用的引力源运行 , 在万有引力的作用下之所以没有最终坠入引力源 , 主要是这个星体拥有着一定的公转线速度 。
之前我写过几篇关于物体围绕引力源公转的文章 , 详细解释了为何这个物体在公转时没有掉下来的原因 , 简单地说 , 可以有两种方法可以进行解释 。 第一种解释就是 , 物体向着引力源的坠落在持续存在 , 只不过由于具有一定的线速度 , 物体在单位时间内在轨道上前进的距离 , 正好与引力源星体表面的弯曲带来的距离拉大效应相抵消 , 坠落和距离拉大的结果相平衡时 , 就会表现出物体沿着特定的轨道围绕引力源运行的状态 。
【如果在月球上瞄准火星开一枪,不考虑阻力影响,能否打到火星?】
第二种解释是 , 根据爱因斯坦广义相对论 , 星体对其它物体所产生的万有引力 , 本质上是时空弯曲的结果 , 星体质量越大 , 时空弯曲效应越明显 , 那么星体周围的物体 , 就会沿着时空弯曲的“界面” , 以测地线(空间中距离最短的两点)的方式运动 。 从物体表面来看 , 其运动轨迹是直线 , 而从第三者来看 , 它的运动轨迹则是沿着弯曲的时空线进行环绕运动 。
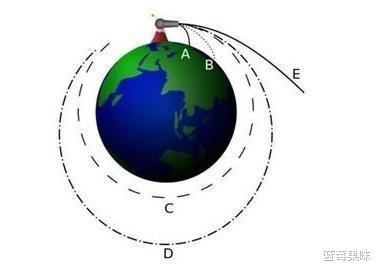
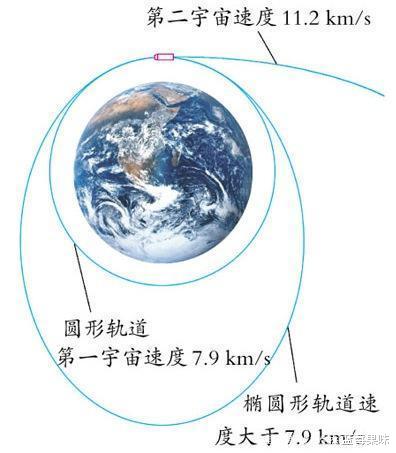
以上两种解释 , 从不同的角度都能对物体可以围绕星体公转的原因进行清晰地说明 。 那么 , 对于这个物体的运动状态来说 , 不同的运动线速度 , 将直接影响到围绕星体运行的最终结果 。 速度过小 , 则“坠落”趋势占据上风 , 物体就会坠向星体的表面;速度过大 , 则万有引力充当的向心力不能完全束缚住这个物体 , 物体就会发生逃逸 。 而能够确保物体不坠落也不逃逸的最低速度 , 则称为这个星体的第一宇宙速度 。 只要物体沿着轨道切向的线速度 , 介于这个星体的第一宇宙速度和第二宇宙速度(最低逃逸速度) , 则物体就会沿着与星体表面一定距离的轨道稳定地公转下去 。
按照星体第一宇宙速度的计算公式V1=√(G*M/r) , 我们可以得出在月球表面 , 一个物体能够围绕它运行的最低速度值为1.68公里每秒 。 而要从月球的表面逃逸出去 , 则最低的逃逸速度值V2=√(2G*M/r)=2.4公里每秒 。 对比地球上发射速度最快的重机枪 , 其子弹速度也只能达到1.5公里每秒 , 所以我们即使不考虑月球上没有空气无法激发的因素 , 在月球上打一枪也不能使其逃脱月球的引力束缚 。
这里需要说明一下 , 有人说即使子弹脱离了月球的引力束缚 , 也逃脱不了地球的引力 , 其实是不准确的 , 按照地球和月球之间的距离38.4万公里来计算 , 在此轨道处物体逃脱地球引力的速度值也只需要1.42公里每秒(月球围绕地球公转的线速度约为1公里每秒) 。 因此 , 只要别向着地球开枪 , 也就是说在月球背向地球的一侧或者正背交界的区域开枪 , 当子弹的速度达到月球的逃逸速度之后 , 自然就会逃逸出地球的引力束缚 。
推荐阅读
- 2022年9月6日我们一起来关注大自然
- 未来人类定居太空要分几步走?国家空间学会制定了太空定居路线图
- 美国在1969年就实现了载人登月,为何过了50多年却难以实现
- 来自月亮的惩罚
- 月球三眼人真的存在?为什么很多人相信月球存在三眼人?
- 每吨191亿元,嫦娥五号带回罕见物质,100吨足够全球人类用1年
- NASA登月计划押宝阿尔忒弥斯火箭 不再由SpaceX一家包办
- 美登月火箭再推迟,重返月球一波三折,为何第二次登月如此不顺利
- 现在火星上的氧气,已够1位宇航员呼吸100分钟



