
文章图片
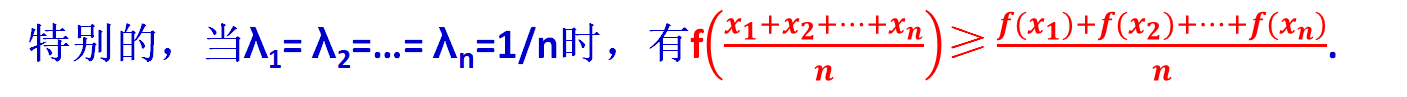
文章图片
凸函数有一个重要的不等式 , 称为詹森不等式 , 又叫做琴生不等式 。
上的凸函数 则对任意xi∈[ab
λi>0(i=12…n) , Σ(i=1->n)λi=1 , 则
当f上凸时 , f(Σ(i=1->n)λixi)>=Σ(i=1->n)λif(xi);
当f下凸时 , f(Σ(i=1->n)λixi)<=Σ(i=1->n)λif(xi).
即 , 闭区间上存在一系数小于1的正数 , 它们的和等于1 。 在闭区间[ab
上的凸函数f(x)上取与这些小于1的正数同样多个自变量 , 分别用这些小于1的正数乘以各个自变量 , 一一对应 , 并求它们的和的函数值;另一方面用这些小于1的正数 , 分别乘以各个自变量的函数 , 保持与前者相同的一一对应关系 , 再求这些函数值的和 。 那么和的函数值与函数值的和有如下的关系:
【凸函数的詹森不等式】当f上
用自己的语言描述一下 , 可以加深印象 。 关于它的证明 , 老黄准备用视频介绍 。 这里主要是介绍它的一个应用 。
我们一般应用得最多的是当λ1= λ2=…= λn=1/n时的特殊情形 。 这时就有:
当f上凸时 , f((Σ(i=1->n)xi/n))>=Σ(i=1->n)f(xi)/n;
当f下凸时 , f((Σ(i=1->n)xi/n))<=Σ(i=1->n)f(xi)/n.
老黄要用它来解决下面的问题:
证明不等式(abc)^((a+b+c)/3)≤a^ab^bc^c 其中abc均为正数.
证:记f(x)=xlnx 则f’(x)=1+lnx f”(x)=1/x>0 f(x)严格凹 (即下凸).
由詹森不等式有:(a+b+c)ln((a+b+c)/3)/3<=(alna+blnb+clnc)/3
即((a+b+c)/3)^(a+b+c)<=a^ab^bc^c.
又(a+b+c)/3>=(abc)^(1/3);
从而有:(abc)^((a+b+c)/3)≤a^ab^bc^c , 得证!
利用詹森不等式解决不等式问题的一般步骤是:
1、构造适合的辅助函数 。 这个辅助函数必须具有凸性 , 这是必要条件 , 并不一定充分 。
2、利用二阶导数判断辅助函数的凸性 , 是上凸还是下凸 。
3、根据
4、转化变形 , 得到要证明的不等式 。
有机会 , 要多运用这个不等式 , 才能发现与之相关的更多规律 。
推荐阅读
- 浙江吴俊东案:好心扶摔倒老人并送医反被告,被法院判决赔偿7万
- 未来人和机器结合变成机械战警?
- 浙江一患者把轮椅带进核磁共振检测室,轮椅被吸到机器上取不下来
- 一女大学生“火”了:化完妆出校,人脸无法识别,网友:太浓了!
- 8年老员工被辞退,临走时老板说出5个字,太现实了!
- 猞猁vs雪豹,当屠狼机器遇到狗熊杀手,谁会笑到最后呢?
- 最真实的元宇宙系统
- 霍金的6个预言:其中3个已经上演,为何警告人类别惹外星人?
- 人类将实现主动进化,和机器融为一体?他是全球首位生化电子人







