一个看似简单实则复杂的悖论，困扰了人类两千多年！
文章图片
文章图片
人类科学发展过程中 ， 总会出现某些矛盾 ， 甚至是哲学上的矛盾 。 其中有一个悖论非常著名：阿基里斯悖论 ， 也被称为“阿基里斯与龟” 。
相信很多人都听过这个悖论 ， 这里简单说一下 。
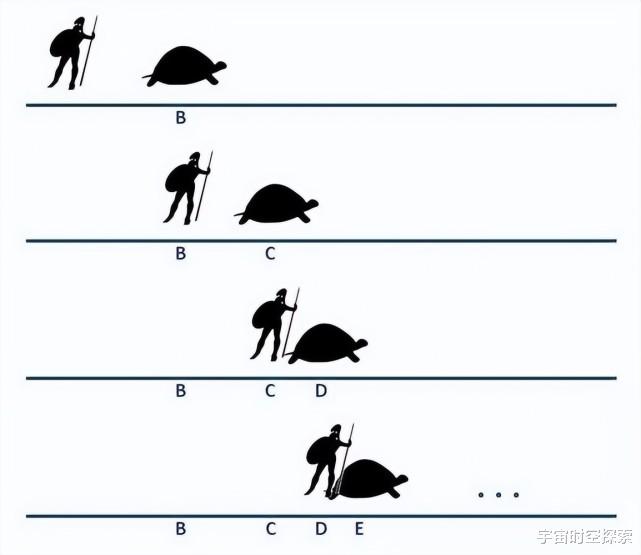
阿基里斯与乌龟赛跑 。 阿基里斯的速度是乌龟速度的十倍 ， 由于乌龟跑得很慢 ， 阿基里斯先让乌龟跑100米 ， 然后再进行比赛 。
接下来会发生什么？
当阿基里斯跑100米的时候 ， 也就是乌龟出发的位置 ， 乌龟跑了10米 。 而当阿基里斯跑10米的时候 ， 乌龟跑了1米 。 阿基里斯跑1米的时候 ， 乌龟跑了0.1米......
可以看出 ， 阿基里斯跑的距离永远是乌龟之前跑的距离 ， 也就是说阿基里斯永远在乌龟的后面 ， 永远追不上乌龟 。
但我们都知道阿基里斯很快就能追上乌龟 ， 这只是简单的数学题 。
这就是阿基里斯悖论 。
类似的悖论还有很多 ， 比如说平时我们经常做鼓掌的动作 ， 假说开始鼓掌时两只手相距1米 ， 当两只手相互靠近时 ， 实际上是两只手之间的距离不断减半的过程 。
最开始是1米 ， 然后是0.5米 ， 0.25米......
也就是说 ， 击掌的动作会有无限多次数的减半过程 ， 你就完不成击掌的动作 。 事实上并不是这样的 。
到底为什么呢？
就如刚才所说 ， 只是简单的数学问题 ， 数学上已经搞定这种问题 ， 只是现实中有时候并不太容易理解 。
数学上是如何解决的呢？
两只手相距1米 ， 然后是0.5米 ， 0.25米......
那么相对左手 ， 右手走过的距离S=0.5+0.25+0.125......
将上面的公式乘以2 ， 我们得到2S=1+0.5+0.25......
下面的公式减去上面公式 ， 很容易得到S=1 。 也就是说 ， 即使是击掌过程经历了无数个过程 ， 走过的距离还是1米 。
当然花费的时间也是如此 ， 假设两只手每靠近0.5米花费1秒 ， 由于会经历无限多个步骤 ， 是不是意味着要花费无限多时间呢？并不是 ， 具体计算过程与上面是一样的 。
在数学上 ， 这样的无限级数被称为“良态” ， 也就是说即便有无穷多个项相加 ， 总和趋近某个数 ， 当有无穷多个数相加时 ， 正好等于那个数 。
但是有限的时间内是如何完成无限多个步骤呢？比如说击掌的过程 ， 有无数个步骤 ， 但并没有最后一步 ， 你是如何完成击掌的呢？
这也是个悖论 ， 困扰了人类两千多年 。
【一个看似简单实则复杂的悖论，困扰了人类两千多年！】如今物理学告诉我们 ， 时间和空间并不是连续的 ， 也不能被无限分割 。 数学上虽然不存在最小的数 ， 但物理和现实中存在最小的时间和空间单位 ， 那就是普朗克时间和普朗克长度 ， 它们是最小的时间和长度单位 ， 任何小于普朗克时间和普朗克长度的时间和长度单位都没有意义 。
推荐阅读
![手机 [观点]折叠屏不是未来 而是末路](https://static.cnbetacdn.com/article/2021/0207/627eba934d86ab0.jpg)
- 有这样一个国家，仅有5个公民，却能让英德和荷兰无可奈何
- 世界上最贵的舌头：身价高达1个亿，一个味蕾就价值8千多
- 63岁大妈雇男保姆仅一个月，却坚定续签一年：我有三方面的理由
- 外媒猜不到它工作原理！嫦娥7的天才设计：月球第一个自由飞行器
- 天狼星的光芒之下，隐藏着一个危险的天体，未来可能会威胁到地球
- 中国十大剧毒蛇之一，一个小时致人死亡，蛇毒却是人类血栓的克星
- 动荡的大脑
- 毒王家族的耻辱？包揽世界毒性前五的家族，会出现一个弱鸡？
- 重庆一个年迈的老奶奶独居，其儿子为了方便，便在家里装了摄像头
- 一个人看不见的“暗物质”