直线斜率公式推导 空间直线的斜率怎么求
当我们爬山时,山越陡,越难爬;骑自行车时,路的坡度越陡,骑起来就越吃力 。飞机的坡度越大,倾斜得越厉害,我们就越难爬起来 。那么,我们如何衡量倾斜的程度呢?
在平面上画一条直线,我们可以直观地看到这条直线的倾斜程度,不难发现,无论直线在哪里,它的倾斜度都是一样的 。
因此,我们可以用一个量来描述整个直线的倾斜度,这个概念被形象地命名为斜率 。
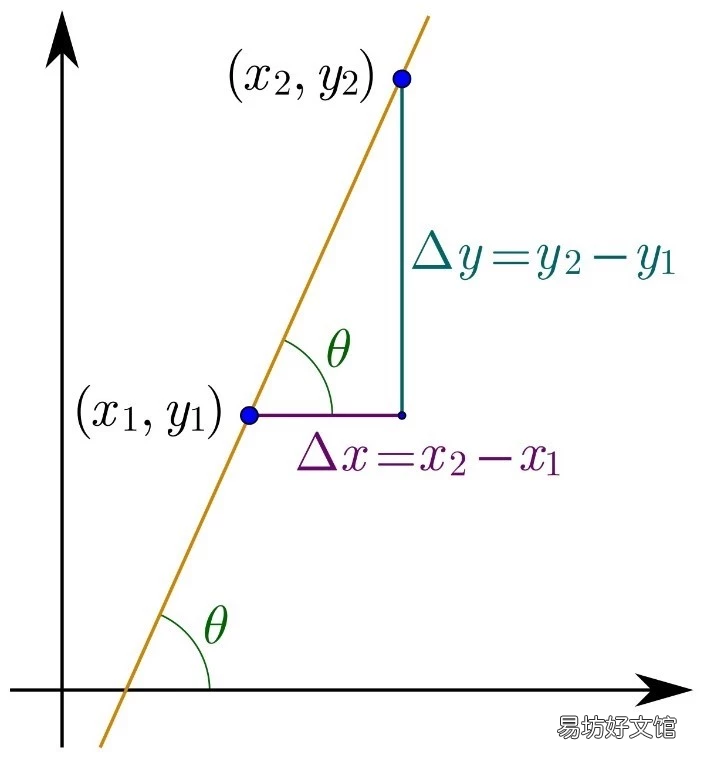
那么,如何计算直线的斜率呢?这个想法也很直观:建立一个坐标系,看看当X轴改变δ x时,Y轴δ y上的直线变化有多大,如果δX是固定的,那么很明显,δY越大,直线越陡,斜率越大 。
文章插图
这和我们判断跑步速度的原因是一样的:给定一个固定的时间,比如10秒(相当于一个固定的δ x),看你能跑多远(相当于δ y),跑得越远(δ y越大),我觉得你会跑得更快 。当然也可以反过来 。给定一个固定的距离,比如100米(相当于δ y),跑得越短(δ x越小),跑得越快 。
结合这两种情况,我们可以发现,无论是固定时间(δx)还是固定距离(δy)好不好,最终的决定因素是δy与δx的比值δy/δx,比值越大,跑得越快,对应的直线越陡 。
因此,我们可以在一条直线上随机找到两点,用它们的纵坐标差δ y与横坐标差δ x之比(δ y/δ x)来定义这条直线的斜率 。
【直线斜率公式推导 空间直线的斜率怎么求】学过三角函数的同学也会知道,这个斜率正好是这条直线与X轴夹角θ的正切值tanθ,也就是tan θ = δ Y/δ X,也就是说直线与X轴夹角θ越大,它的斜率越大,倾斜越多,这和经验是一致的 。
推荐阅读
- 成本费用利润率的意义 成本费用利润率计算公式
- 工程量计算 梯形体积
- 高中万有引力的公式大全 万有引力常数
- 中位数的概念及公式 中位数的概念
- 数学直接开平方公式 如何开平方
- 物质的量浓度计算 物质的量浓度公式
- 百分比的计算公式 百分比的算法
- 梯形田地如何计算亩数公式?
- 功率计算公式 欧姆定律公式
- 高数弧长ds的三种公式 求弧长公式







