爱因斯坦场方程，它是如何将时空的形状与物质的分布联系起来的？ _卫星

文章图片

在爱因斯坦的广义相对论中，场方程将时空的几何形状与物质的分布联系起来。 1915年，爱因斯坦首次发表了这（些）方程，将局域时空曲率（由爱因斯坦张量表示）与局域能量、动量和该时空内的应力联系起来。但这意味着什么？为什么它对广义相对论的原理很重要？我希望本文能把这解释清楚。

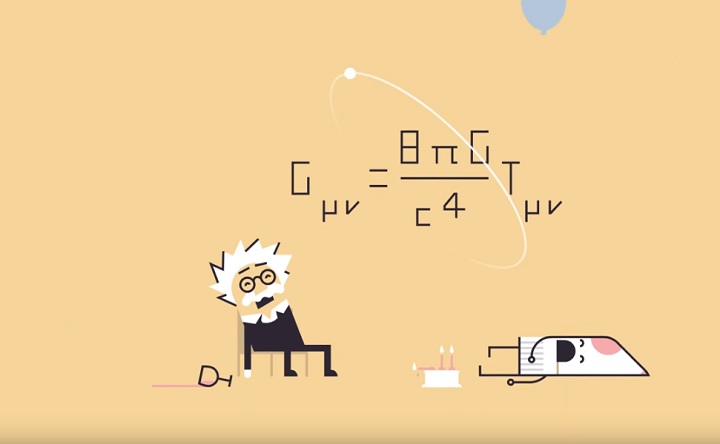
爱因斯坦场方程，虽然是复数，但可以统称为一个方程：

著名的场方程将质量和时空曲率联系起来。

这一个方程是如何定义构成广义相对论基础的一整套方程的？下标μ和ν取不同的数值，它们可以取4个值。 μ ，ν∈{0123 。
μ和ν的每一个组合表示一个不同的场方程。每一个都对应不同的曲率现象。在我们深入研究每一项代表什么之前，另一件值得强调的事情是我们处理的是被称为张量的量。 G下标是一个张量， g和T下标也是一个张量。张量是非常有趣的数学对象，但在这篇文章中我们不会深入探讨它们。我们将把它们简单地当作矩阵。

紫色的是张量元素；黑色的是某个常数

mu和nu是任意的，

爱因斯坦场方程中的张量是由4x4矩阵表示的。下标0、1、2和3分别表示建立广义相对论的四个不同维度：三个空间维度和一个时间维度。 0表示时间维度， 1、2、3表示我们喜欢的笛卡尔系统（分别是x、y和z）。
问题来了，每个张量代表什么？
我们要看的第一个张量是T_μν 。它被称为应力-能量张量。本质上，它包含了我们选择研究的时空区域中“物质”分布的信息。在很多情况下，这个时空“区域”实际上是整个宇宙。这个张量描述了时空中能量和动量的密度和通量。它是物质、辐射和非引力场的属性。简单说，通量是一个量，表示有多少场（量）通过了空间的某个区域。在这种情况下，我们特别关注的是能量的流动。也就是，能量是如何在时空中分布的。本质上，这也代表了质量（因为质能等价）。
应力-能量张量可以表示为：

红色项代表能量密度除以光速的平方。橙色项代表动量密度，即相对论质量的通量。
绿色和紫色一起表示动量通量，即：

也可以把动量通量分解，得到另外两个分量，绿色的代表剪应力，紫色的代表压强。

蓝色表示的是能量通量，即：

所有这些术语（应力、压力、动量通量、能量通量和能量密度）都是物质和能量如何在时空中分布的表示。
我们再看方程的另一边。如果应力-能量张量T包含物质如何分布的信息，那么完全有理由假设左边一定包含时空如何弯曲的几何信息。 G张量，称为爱因斯坦张量，包含时空曲率的信息。场方程告诉我们物质和能量的分布如何扭曲时空；也可以反过来说，时空的扭曲如何影响物质和能量的分布。这些场方程确切地告诉我们，某些质量如何以特定的方式扭曲时空，以及物体在时空中的行为。
爱因斯坦张量（G）是其他一些张量相当复杂的形式，比如里奇张量和度规张量（我们也在第二项g中看到）。我暂时不会讲太多细节。