
文章图片

文章图片
文章图片
大家都知道黑洞能吞噬一切 , 而“不会断的绳子”和“吞噬一切的黑洞”这样的命题就像是矛和盾一样 , 是无解的问题一般 。 矛盾遇到一起 , 最后是两败俱伤 , 但这个两败俱伤的结论放到黑洞身上并不合适 , 因为就史瓦西黑洞而言 , 只要绳子进入黑洞 , 那么绳子所连接着的一切都会被拉进黑洞(谁叫你假定绳子不会断了) , 绝无半点妥协可言 。
史瓦西黑洞诞生于广义相对论的第一个精确解 , 这是德国物理学家史瓦西在爱因斯坦的广义相对论发表后不久解出来的 。 这个精确解描述了一个无自转、不带电的天体 , 对星外时刻的影响 , 后来随着对这个解的深入研究 , 科学家发现存在一个被称为史瓦西半径的范围 , 如果一个天体 , 其全部质量都被集中到了其自身的史瓦西半径以内 , 那么它将会成为一颗黑洞 , 叫做史瓦西黑洞 。
该黑洞也是人类最早发现的一种黑洞 , 由于其简单的结构 , 由中心奇点和事件视界(和史瓦西半径重合在一起)组成 。 而事件视界以内被称为单向膜区 , 顾名思义 , 任何越过事件视界的物体都只能前进不能后退 。
如果用牛顿力学和万有引力定律进行一个不太严谨的描述 , 在史瓦西黑洞表面 , 即事件视界上 , 该处的逃逸速度为光速 , 也就是一个进入史瓦西黑洞的物体 , 如果想要逃离黑洞 , 就必须加速到光速以上才有可能 , 但狭义相对论的光速不变原理又规定了 , 任何物体的速度不得超过光速 , 那么结论就是:没有物体能够逃离光速 。
但实际上这个说法仅仅只能作为一个粗糙的解释 , 因为牛顿力学与狭义相对论本身就是一个从属的关系 , 而万有引力定律和广义相对论也是从属关系 , 狭义相对论与广义相对论分别在低速、弱引力场的环境下都可以与牛顿力学与万有引力定律近似相等 。
所以说按照广义相对论的说法 , 自然是要用到单向膜区这样的术语了 , 不过还有一种更加通俗的说法 , 那就是利用光锥的性质 , 我相信不少人都有听过“光锥之内皆命运”这句话吧 , 如果这句话用狭义相对论来解释的话 , 光锥之外的事物 , 其速度都是超光速的 , 而超光速是不可能的 , 所以光锥之外的世界不属于我们 。
所以说现实世界中的物体 , 其发展都逃不出光锥之外 , 所以我们可以利用光锥的朝向 , 来判断物体的发展方向 , 比如说黑洞 , 通过时空图我们可以发现 , 所有进入事件视界的物体 , 其光锥朝向都是清一色的向内 , 也就是朝着奇点出发 , 很显然 , 由于这一性质 , 我们可以毫无顾忌的判断 , 所以物体都必须坠落奇点 。
有了这个结论 , 我们对于绳子和黑洞之间的关系就有了更加明确的态度 , 虽然你绳子坚不可摧 , 但是史瓦西黑洞内部的性质规定了你必须朝着我奇点坠落 , 正因为这一点 , 绳子的优点反而成了要命点 , 因为绳子不会断开 , 所以绳子上所连接的一切物体都会被毫无情面的拉进黑洞 , 更不用说事先用绳子捆住的那个人了 。
这就是这个问题发生在史瓦西黑洞上的情况 , 但先前也提到了 , 史瓦西黑洞并不是全部黑洞的代表 , 那么接下来我们就来简单看看旋转黑洞的表现(史瓦西黑洞是无自转的黑洞) 。
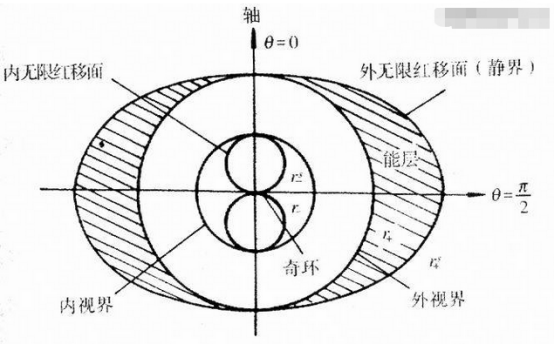
旋转黑洞在结构与史瓦西黑洞是不一样的 , 视界并不是它的最外层结构 , 一个叫做“静界”的结构才是它的表面 , 相比于视界的不留情面而言 , 静界就要温和多了 , 它的特性表现为所有越过静界的物体 , 在没有抵达视界之前 , 都必须持续运动 , 也就是说在里面的物体都必须动起来(这也是它叫做静界的原因 , 是划分物体能否静止的分界线) 。
虽然在里面的物体必须持续运动 , 但并没有要求物体必须进入视界 , 也就是说如果物体拥有足够强大的动力 , 那么是可以逃出静界的 , 也就是逃出了旋转黑洞 , 那么对于这条坚不可摧的绳子来说 , 只要外界提供足够强大的拉力 , 那么绳子就可以带着它捆住的那个人一起逃离旋转黑洞 。
推荐阅读
- 黑洞未解之谜:究竟是谁制定了这些规则规律
- 我们可以通过引力波在黑洞周围发现新的粒子种类
- 太阳系隐藏着什么?是黑洞吗?其实九号行星之谜比你想象的要多
- 黑洞吞噬恒星过程,就像黑洞在吃“意大利面”?
- 黑洞的死亡,白洞是如何形成的?
- 一束光线的命运,关闭手电筒光源后,光线会消失还是继续传播?
- 距地球50亿光年,爱因斯坦十字真的出现了!怎么理解这一现象?
- 太阳上出现巨大“黑洞”:24小时急速扩大一倍,尺寸达地球的3倍
- 有人认为银河系中心可能不是真的黑洞,而是暗物质,这可能吗?







