序列|拓端tecdat|Python用ARIMA和SARIMA模型预测销量时间序列数据_预测|df|数据|时间|销量|季节性

原文链接：http://tecdat.cn/?p=21573
介绍
ARIMA模型是时间序列预测中一种常用的统计方法。指数平滑和ARIMA模型是时间序列预测中应用最为广泛的两种方法，它们是解决这一问题的补充方法。指数平滑模型是基于对数据趋势和季节性的描述，而ARIMA模型则是为了描述数据的自相关性。
在讨论ARIMA模型之前，我们先来讨论平稳性的概念和时间序列的差分技术。
平稳性
平稳时间序列数据的性质不依赖于时间，这就是为什么具有趋势或季节性的时间序列不是平稳的。趋势和季节性会在不同的时间影响时间序列的值，另一方面，对于平稳性，当你观察它时并不重要，它在任何时间点看起来都应该是相同的。一般来说，一个平稳的时间序列在长期内没有可预测的模式。
ARIMA是自回归综合移动平均线的缩写。它是一类在时间序列数据中捕获一组不同标准时间结构的模型。
在本教程中，我们将讨论如何用Python开发时间序列预测的ARIMA模型。
ARIMA模型是一类用于分析和预测时间序列数据的统计模型。它在使用上确实简化了，但是这个模型确实很强大。
ARIMA代表自回归综合移动平均。
ARIMA模型的参数定义如下：
p：模型中包含的滞后观测数，也称为滞后阶数。
d：原始观测值的差异次数，也称为差分阶数。
q：移动平均线窗口的大小，也叫移动平均阶数。
建立一个包含指定数量和类型的项的线性回归模型，并通过差分程度来准备数据，使其平稳，即去除对回归模型产生负面影响的趋势和季节结构。
步骤
1可视化时间序列数据
2确定日期是否平稳
3绘制相关图和自相关图
4根据数据建立ARIMA模型或季节ARIMA模型
在本教程中，我正在使用下面的数据集。

df.head()
#更新表头
df.columns=["月份","销量"]
df.head()
df.plot()

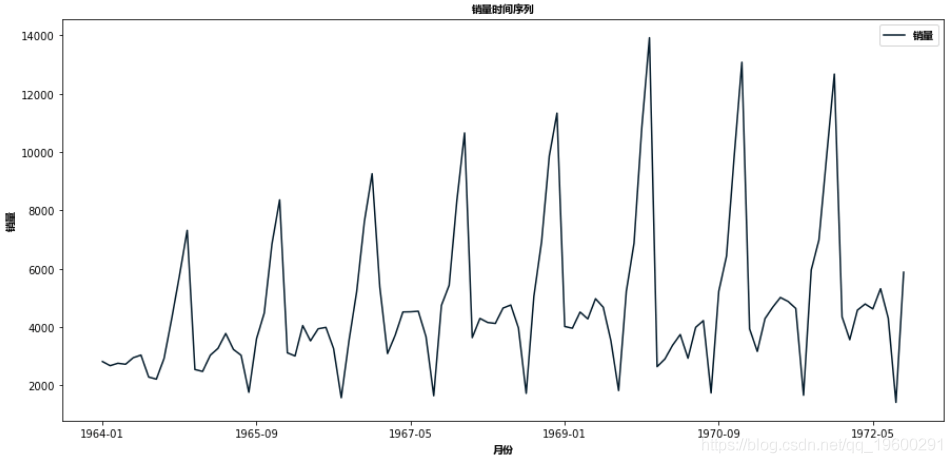
序列|拓端tecdat|Python用ARIMA和SARIMA模型预测销量时间序列数据

文章图片

如果我们看到上面的图表，那么我们将能够找到一个趋势，即有一段时间销售很高，反之亦然。这意味着我们可以看到数据是遵循季节性的。对于ARIMA ，我们首先要做的是确定数据是平稳的还是非平稳的。如果数据是非平稳的，我们会尽量使它们平稳，然后我们会进一步处理。
让我们检查给定的数据集是否是平稳的，为此我们使用adfuller检验。
我通过运行上述代码导入了检验函数。
为了确定数据的性质，我们将使用零假设。
H0:零假设:这是一个关于总体的陈述，要么被认为是正确的，要么被用来提出一个论点。
H1:备选假设:与H0相矛盾，当我们拒绝H0时，我们得出的结论。
Ho:它是非平稳的
H1:它是平稳的
我们将考虑数据不平稳的零假设和数据平稳的备择假设。

adfuller_test(df['销量'])

运行上述代码后，我们将得到P值，

ADF Test Statistic : -1.833
p-value : 0.363915
#Lags Used : 11
Number of Observations : 93

这里P值是0.36 ，大于0.05 ，这意味着数据接受了零假设，这意味着数据是非平稳的。
我们来看看一阶差分和季节性差分：
df['Sales First Difference'] = df['销量'] - df['销量'].shift(1)

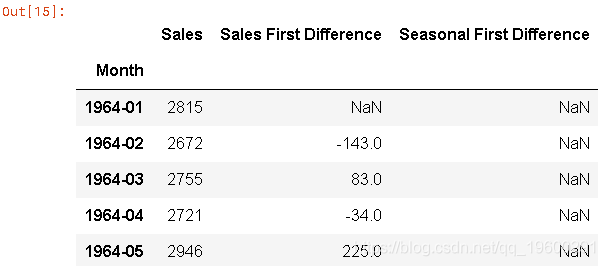
文章图片

# 再次测试数据是否平稳
adfuller_test(df['Seasonal First Difference'].dropna())
ADF Test Statistic : -7.626619157213163
p-value : 2.060579696813685e-11
#Lags Used : 0
Number of Observations : 92

这里p值是2.06 ，表示拒绝零假设。所以数据是平稳的。

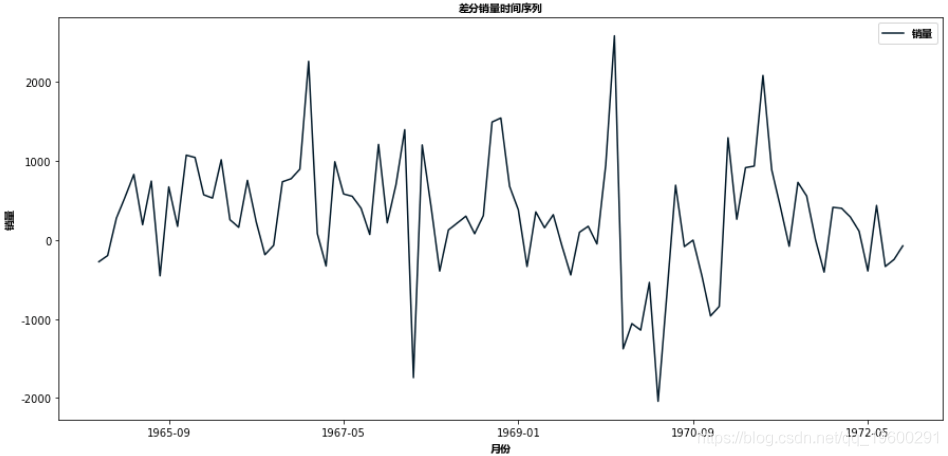
文章图片

自相关系数：

autocorrelation_plot(df['销量'])
plt.show()

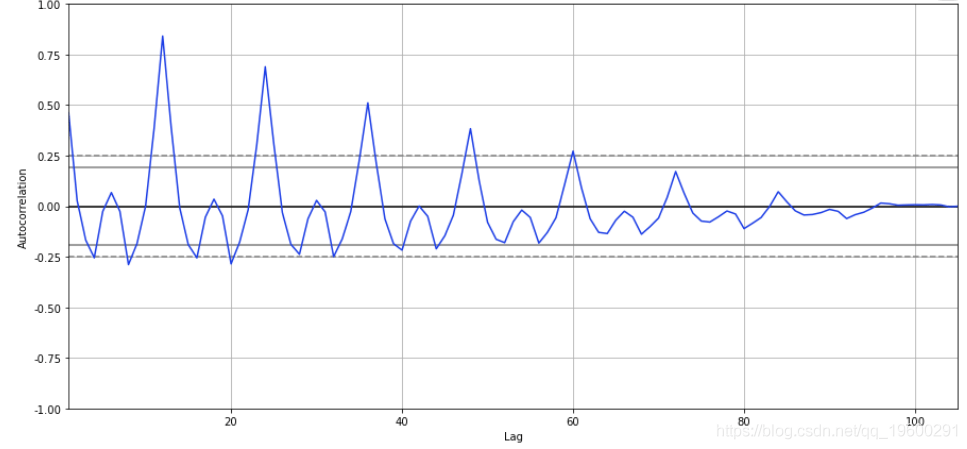
文章图片

plot_acf(df['季节性一阶差分'].dropna(),lags=40,ax=ax1)

文章图片

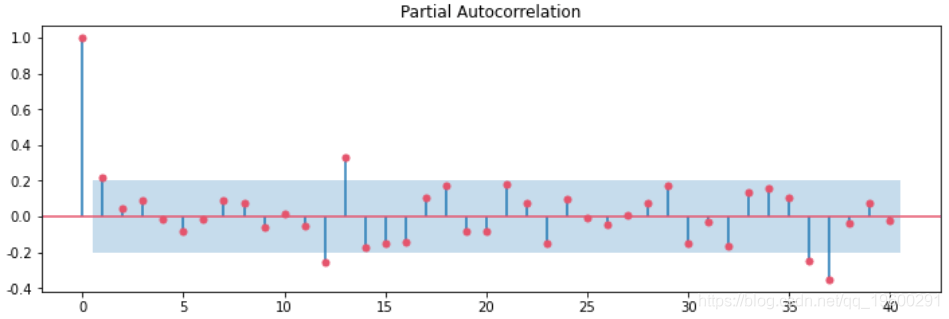
文章图片

建立ARIMA模型

#对于非季节性数据
#p=1, d=1, q=0 or 1
model=ARIMA(df['销量'],order=(1,1,1))

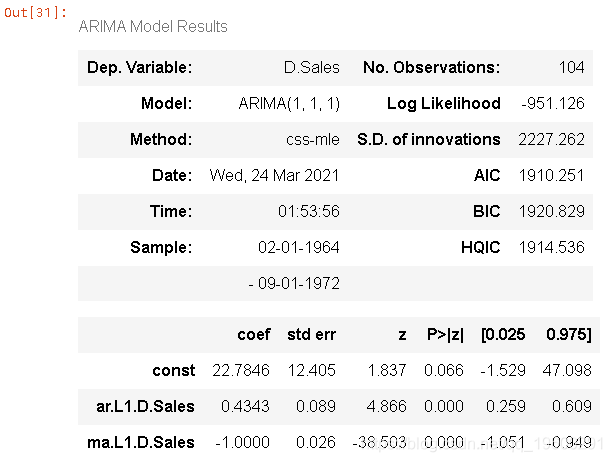
文章图片

predict(start=90,end=103,dynamic=True)

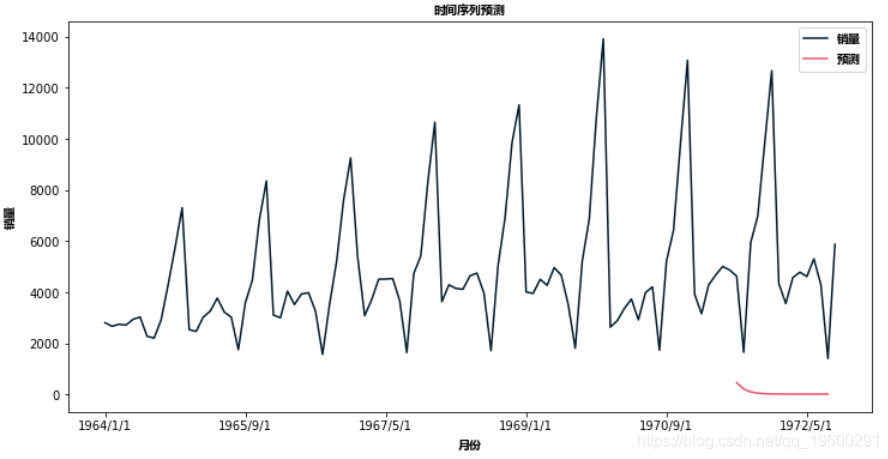
文章图片

SARIMA模型然后建立SARIMA模型

plot(figsize=(12,8))

文章图片

可以看到拟合效果要优于ARIMA模型。
然后我们用SARIMA模型对未来进行预测。

future_df['预测'] = results.predict(start = 104, end = 120, dynamic= True)
future_df.plot(figsize=(12, 8))

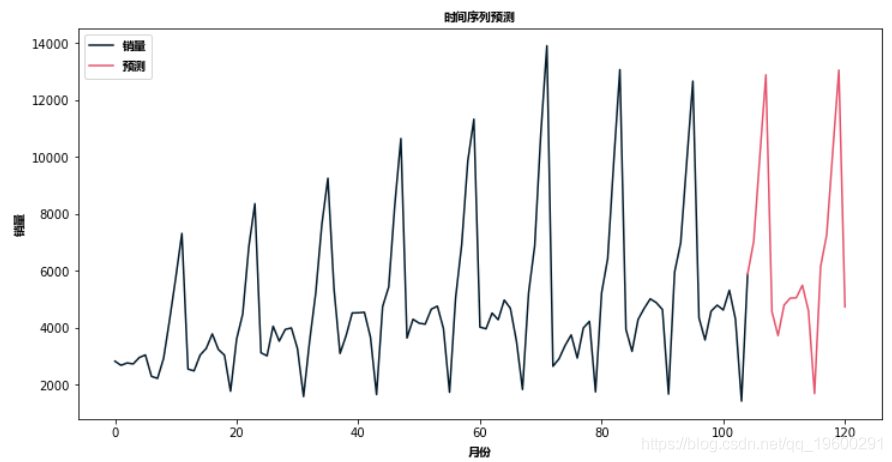
文章图片

结论时间序列预测是非常有用的，有很多其他模型可以做时间序列预测，但ARIMA是很容易理解的。

文章图片

最受欢迎的见解
1.在python中使用lstm和pytorch进行时间序列预测
2.python中利用长短期记忆模型lstm进行时间序列预测分析
3.使用r语言进行时间序列（arima ，指数平滑）分析
4.r语言多元copula-garch-模型时间序列预测
5.r语言copulas和金融时间序列案例
6.使用r语言随机波动模型sv处理时间序列中的随机波动
7.r语言时间序列tar阈值自回归模型
8.r语言k-shape时间序列聚类方法对股票价格时间序列聚类
【序列|拓端tecdat|Python用ARIMA和SARIMA模型预测销量时间序列数据】9.python3用arima模型进行时间序列预测