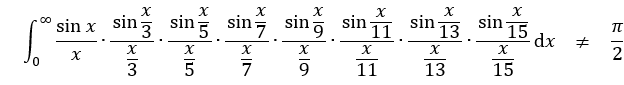数学|逼死强迫症的博尔维恩积分_

学过微积分的读者都知道，求导数有一定之规，但求积分则可能会出现各种神奇的结果。今天介绍博尔维恩积分（）。这是一组积分等式：

数学|逼死强迫症的博尔维恩积分
本文图片

看到这里，读者可能会将这个形式推广下去。但令人意外的是，这个系列到此中断。我们得到

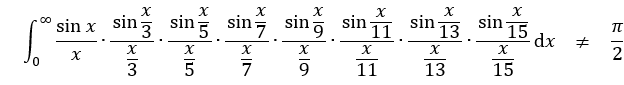
本文图片

它的精确值是一个很奇怪的数：

本文图片

这个意外的结果是博尔维恩父子：大卫·博尔维恩（David Borwein ， 1924–）和乔纳森·博尔维恩（Jonathan Borwein ， 1951–2016）在 2001 年提出来的。大卫·博尔维恩的另一个儿子彼得（Peter B. Borwein ， 1953－2020）也是一位数学家，可以称为一个数学之家了。比较嘘唏的是两个儿子都先老父而去。
小博尔维恩在数学软件上“验证”了他们的结果后，跟的开发人员开了一个玩笑 — 他说出了一个“bug” 。可怜的计算机代数专家花了三天时间去找 bug ，终于意识到这只是一个玩笑。
产生这个结果的原因可以用卷积和傅立叶变换来解释。我们不深入讨论。一般地，考虑如下的积分：

其中 , , , ..., 是实数。那么上式中的值可以用这些参数来表达。这个表达式的一般描述有点复杂。我们只考虑一个特殊情况。假定我们有

数学|逼死强迫症的博尔维恩积分
本文图片

也就是说，是第一个使得超过的那个指标。那么有 , , ?, ，及

本文图片

博尔维恩积分就是这个结果当时的特例。读者可以自行验证。
还有一个类似的例子更为离奇：

本文图片

这个系列可以推广到：

数学|逼死强迫症的博尔维恩积分
本文图片

但只是对成立。在此之后的都不成立。这个结果是澳大利亚科普作家和趣味数学家格雷格·伊根（Greg Egan, 1961?）给出的。见约翰·拜艾兹（John C. Baez, 1961?）的博客。这个例子说明了盲目的推演是危险的。这样的例子还有拉马努金计算的，这个数几乎就是一个整数，距离整数只有的误差。再比如，等式几乎成立，误差到了小数点后位。这个结果是博尔维恩兄弟俩的结果。
上面的积分都只涉及正弦函数。下面的例子多了因子，结果也会在某一步不再成立：

数学|逼死强迫症的博尔维恩积分
本文图片

如此整齐的公式却在某一行突然出现奇怪的数字，强迫症直呼受不了。参考文献