高维空间的神器！地球上所有的水，都装不满“克莱因瓶”吗？克莱因瓶

文章图片

大家都知道，人类作为三维世界的生物是无法感知到高维空间的，我们只能费尽心思地去设想。此前，著名数学家就设计出了一种瓶子，这个瓶子有着无定向的平面，名叫克莱因瓶。

克莱因瓶
在不少人眼中，这个瓶子是高维空间的神器，并且，据说将地球上所有的水放进去，都装不满“克莱因瓶” ，这是为什么呢？就让我们一起来看看吧！
克莱因瓶是什么？首先咱们要了解一下到底什么是克莱因瓶。这是德国数学家菲利克斯·克莱因在1882年时发现的，德语的称呼本来是“克莱因平面” ，但是由于翻译问题，被误翻成了克莱因瓶。不过这个“克莱因平面”的外观看起来确实和瓶子很相似，所以这个误称也就被沿用了。

菲利克斯·克莱因
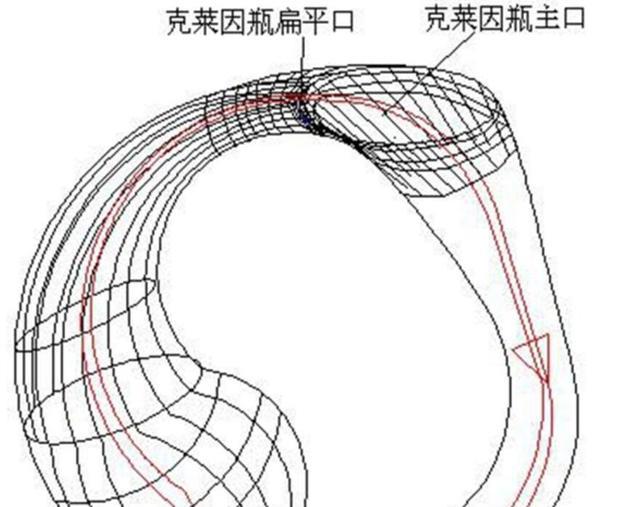
从本质上来说，克莱因瓶是没有边界的，并且其结构看起来也比较简单。在瓶子的底部有一个洞，而瓶颈被拉长之后，会扭曲地插入瓶内，最终再与底部的洞相连。在这种情况下，并没有内部和外部的区别。
说到这儿，大家应该想到了另一个有类似结构的东西，那就是莫比乌斯带。莫比乌斯带制作起来要比克莱因瓶简单，并且它是通过二维来展示三维的，所以在我们看来还可以接受。

莫比乌斯带
而如果你将两条莫比乌斯带粘在一起，就能得到一个没有边的闭合曲面，这就有些类似于克莱因瓶了。

科学家表示他们将这种局域具有欧几里得几何的曲面称之为拓扑流形，莫比乌斯带和通常的纸环都是带边的流形，而它们粘合而成的克莱因瓶和环面(torus)是不带边的闭合流形。

可克莱因瓶却试图向我们展示四维空间，因此它看起来才比较“怪异” 。值得一提的是，其实现在市面上所制造的所有克莱因瓶都不算是真的，因为我们无法跨越维度造出这种高维空间的神器，就像如果你身处二维世界，就无法造出三维的球体一样，这就是限制。

克莱因瓶模型
不过，为什么说就算将地球上所有的水都灌入，也无法塞满这个瓶子呢？难道说这个瓶子还有着无底洞的性质？
克莱因瓶与水大家都知道，从目前的观测来看，地球除了名字里不带水以外，确实是太阳系内水源最丰富的存在。所以从表面上来说，装满这样一个小小的瓶子还是很容易的。既然这样，为什么会说装不满呢？
这是因为在瓶子的底部存在着一个漏洞，而克莱因瓶的内部本身就存在着“循环” ，因此实际上在四维的建模当中，水流从头到尾都没有流过瓶子的表面。由于表面没有“终结” ，所以瓶子永远不会装满。

克莱因瓶接口
需要注意的是，这个永远不会装满是有限制的，单指在三维空间当中。如果可以进入四维空间，并且使用克莱因瓶的话，那么还是能够轻松就将其装满的。可见克莱因瓶无法被装不满的根本原因在于，这东西原理根本就不属于三维空间，当然不受限于三维空间的“容量体积”的限制规则。

克莱因瓶，永远不会装满
值得一提的是关于克莱因瓶装水这件事情，还曾有过不同的说法。那就是因为这个瓶子没有内外之分，导致它与球面和环面不同，因此它虽然是封闭的曲面，却无法被当成容器来盛水。
总之不论是哪一种解释，都与克莱因瓶本身的特性有关系，我们很难说哪一种是正确的。