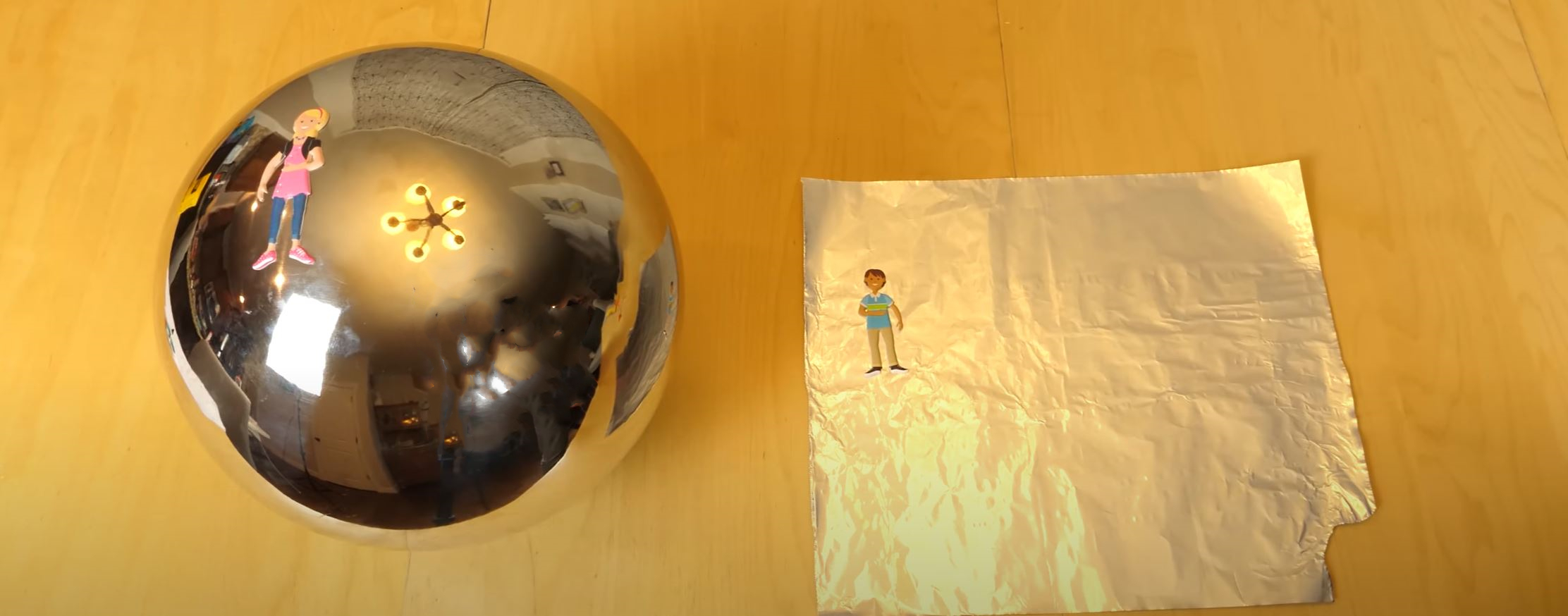
文章图片
假如有生活在
【假如存在二维生物,他们如何辨别所处的面是平面还是曲面】
我们从数学上可以知道 , 在平面中三角形的内角
但是 , 如果不仔细思考而简单地实施这些方法 , 我们会发现得到了错误的结论 。 以我们的地球为例 , 我们知道地球表面是一个球面 , 但是我们平时所见到的却是平坦的 , 如果我们在这上面画三角形 , 我们也会发现它的内角和为180度 。 如果按照上述方法 , 我们应该得到我们所生活的表面是一个平面而不是球面 。
人的渺小对比地球之大 , 我们所生活的表面确实可以看成是曲率为0的平面 , 但这离真相还相差十万八千里 。 为了更好地利用上述数学知识来揭开真相 , 我们需要避免让三角形只存在于局域之中 , 而是尽量让它处于全局之中 , 这样才能发现三角形的内角和并不等于180度 , 我们所生活的表面是曲率不等于0的曲面 。 二维生物也要注意到这个细节 , 他们才能得出真相 。
同理 , 我们想要测量出宇宙是平坦的还是弯曲的 , 也不能局限于某个区域 。 除了我们刚才所讲的这种局域的效应之外 , 质量的存在也会弯曲周围的局部空间 , 造成测量出的结果更不准确 。 因此 , 科学家在测量宇宙的形状时 , 会使用更广阔的宇宙空间 。
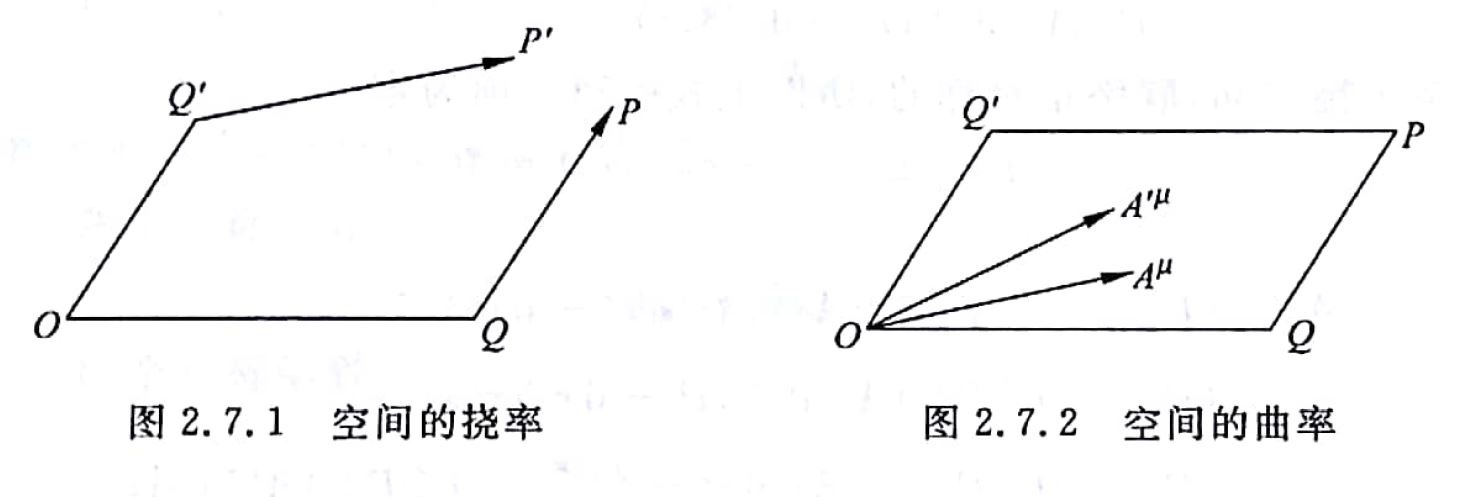
事实上 , 空间除了弯曲之外 , 还可以扭曲 。 弯曲用曲率来表示 , 扭曲用挠率来表示 。 如下图所示 , 有OQ和OQ'两个向量 , 它们分别沿着对方的方向平移 , 如果空间存在扭曲 , 则平移后的P点和P'点并不会重叠在一起 。
在广义相对论中 , 一般不考虑挠率的存在 , 因为这会使问题变得更加复杂 , 而且得出的结论在实际观测中也没有出现 。
推荐阅读
- 又靓又能做科研,这位博士小姐姐,发完Science发Nature!
- 是的,我相信
- 38亿光年外发现罕见「五重奏」,空间强烈扭曲,爱因斯坦又对了?
- 早年:不明飞行物曾冲向国际空间站
- Nature:衰老的根源在核糖体?衰老加剧核糖体暂停,破坏蛋白质稳态
- Nature:新冠实际死亡人数或已超千万
- 袁隆平对转基因的态度:从来未曾中立,不卖粮给中国,咱就麻烦了
- 汤加火山爆发:地球一个响指,万物之灵跌下山巅
- “走蛟”真的存在吗?为何蛇的数量如此多,却很少看到蛇的尸体?







