地球那么大，人们是怎么测得它的“重量”的？ _引力常量

文章图片

文章图片

阿基米德曾说，给我一个支点，我就能撬起地球！假设他体重100kg ，而地球的质量是6×10^24kg代入原理公式：
100×动力臂=6×10^24×阻力臂
动力臂=6×10^22×阻力臂

由此可见，要找到一个非常长的杆子，然后找一个支点，而且还要使得动力臂的长度是阻力臂的6万亿亿倍。也就是说如果阻力臂是1米，那动力臂就是6万亿亿米。先不说阿基米德能不能把这个杆支到地球上，若他一分钟走100米。走到杆的另一端就需要约12万亿年。

而若他将地球撬动1厘米，阿基米德就要推着杠杆走6千万亿公里，地球跟太阳的距离约1.5亿公里，也就是他要在地球和太阳之间走2千多万个来回。除非他长生不老，否则不可能完成。抛开他能不能撬动的因素，这里有个问题就是地球那么大，它的重量人们如何测得？接下来讨论这个问题！
牛顿万有引力定律牛顿总结的三大定律和万有引力定律写入了《自然哲学的数学原理》中。

万有引力的表达式F=GMm/R2=mg我们可以变形为M=gR2/G ，在地球表面可以近似认为万有引力提供重力加速度，我们只要测的某个物体的万有引力常数G和地球的半径R以及重力加速度g ，就可以知道地球的质量M ，那么这三个物理量如何获得？
卡文迪许扭秤实验测得引力常数牛顿虽然用严谨的数学推出了万有引力，却始终没能得出万有引力公式中引力常量G的具体值。因为对于一般物体而言，它们的质量太小，在实验中很难准确测出它们之间的引力：而天体之间的引力很大，却又很难准确测出它们的质量。

直到一百多年后，卡文迪许成功利用扭秤给G定量，这才使万有引力定律形成了一个完善的等式。否则，万有引力或许就失去了应用价值，毕竟当时连牛顿自己也无法利用万有引力公式计算出地球的质量。从这个角度看，万有引力的真正意义就在于万有引力常数。 1789年，卡文迪许机智地利用光的反射，巧妙放大了微弱的引力作用。
【地球那么大，人们是怎么测得它的“重量”的？】
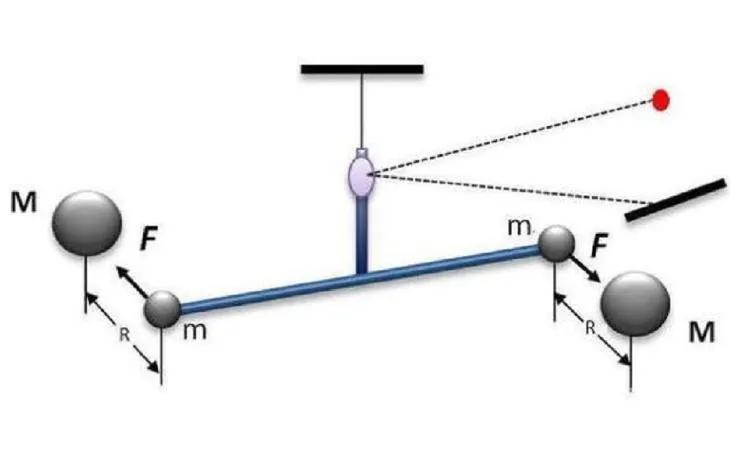
他将两个质量相同的小铁球m分别放在扭秤的两端，扭秤中间用一根韧性极好的钢丝把一面小镜子系在支架上，然后用光照射镜子，光便会被反射到一个很远的地方，这时要做的就是立马标记光被反射后出现光斑的位置。
接着，用另外两个质量相同的大铁球m同时吸引扭秤两端的小铁球m 。在万有引力作用下，扭秤会微微偏转，光斑的位置却移动了较大的距离。由此，卡文迪许测算出了万有引力公式中的引力常数G为6.754×10-11N·m/kg 。
这个数值G至今仍十分接近国际的推荐标准G=6.67259×10（－11）N·m2/kg2(通常取G=6.67×10（－11）N·m2/kg2) 。在这之后，对于两个物体之间的万有引力。

F1、F2：两个物体之间的引力。
G：万有引力常量。
m1：物体1的质量。
m2：物体2的质量
r：两个物体(球心)之间的距离。
依照国际单位制规定， F的单位为牛顿(N) ， m1和m2的单位为千克(kg) ， r的单位为米(m) ，常数G近似于6.67×10（－11）N·m2/kg2 。从上述公式中，我们可以直观地看出引力只与物体的质量、距离有关！
地球周长的测量埃拉托斯特尼（公元前276-前195年），作为亚历山大图书馆的三代目馆长，首先是一位地理学家，天文学家，也是一位数学家。

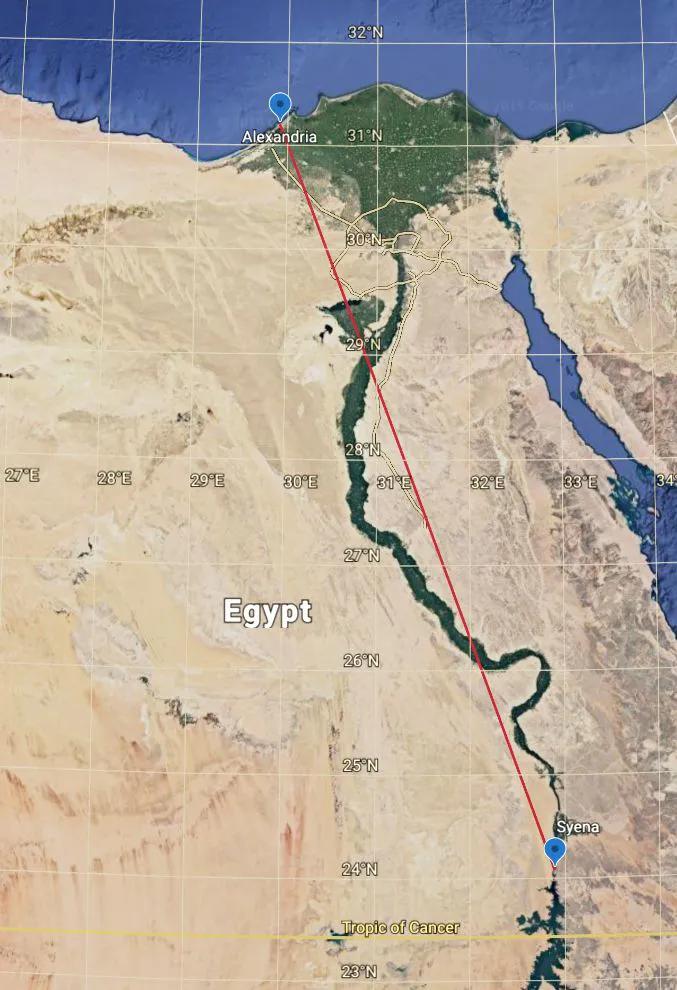
作为地理学家，他整理了埃及和希腊的地图测绘，描绘出了一张当时的世界地图，被后人复原后，是这个样子的：

注意看上面那张“世界地图”里的埃及尼罗河三角洲和沿岸。埃及的测绘工作早就被埃及人完成了，可能是西方世界当时被测的最为准确的部分了。从亚历山大港到尼罗河上游的Syena ，也就是今天的阿斯旺的直线距离，也被埃拉托斯特尼很好地计算了出来:

地球那么大，人们是怎么测得它的“重量”的？

推荐阅读

生日骚祝福短句

泸州老窖特曲

抖音视频最长多长时间抖音视频最长多长时间可以删除

饮食误区吃的好身体就健康

法国的的冰酒产区？

施肥是大蒜生长的关键

男人做5件事证明他真爱你

铁犁是什么时候发明的

如何在旅途中更好地欣赏美景？

拨号显示未在网络上注册

熬粥的时候，最上边的一层浮膜是啥

男生网名两个字简单唯美

春节的来历15字 15字春节的来历

宝宝老摇头的原因

躺着睡觉能减肥吗？怎么睡觉能减肥？

下列凭证属于外来原始凭证的有

新湖南XHN 惊蛰至，一起来的还有今年首场强对流天气

连接器是什么东西

孩子大便干怎么办

旅游的时候你捡到五万人民币，你会自己花这笔钱吗？为什么？