历史表明 , 人类接受一种新数的过程是漫长而坎坷的 。
正数、负数、有理数、无理数
在欧洲 , 负数的概念迟至12世纪末 , 才由意大利数学家莱昂纳多·斐波那契(Leonardo Fibonacci , 约1170—约1250)做出正确的解释 。 但直到18世纪 , 欧洲仍有一些学者认为负数是“荒唐、无稽的” 。 他们振振有词地说 , 零是“什么也没有” , 那么负数 , 即小于零的数是什么东西呢?难道会有什么东西比“什么也没有”还要小吗?!
本文图片
无理数的出现 , 可以追溯到相当久远的年代 。 大约公元前5世纪 , 毕达哥拉斯学派的门人希帕斯发现 , 等腰直角三角形的斜边与直角边的比不可能表示为既约分数(即几何上的“不可公度”) 。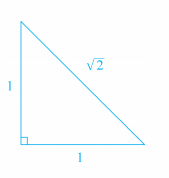
本文图片
希帕斯的思路说来也简单 , 他采用了“反证法” , 即先假设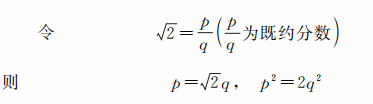
本文图片
显然 , p必须是偶数 , 否则左式绝不等于右式 。 现令p=2p′(p′为整数) , 代入得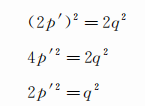
本文图片
这意味着q也必须是偶数 , 否则右式绝不等于左式 。 这样 , p与q便至少有一个2的公因子 , 它与
希帕斯的证明引起了毕达哥拉斯学派的恐慌 , 因为这个学派抱定“两条线段一定可以公度”的教义 , 他们宁可拒绝真理 , 也不愿放弃错误的信条 , 他们容不得希帕斯这样的“异端邪说” 。 可怜的希帕斯终于被毕达哥拉斯学派的忠实门徒 , 抛进大海喂了鲨鱼 。
本文图片
人类认识无理数的过程 , 要比想象的更加漫长和曲折 。 从希帕斯起至基础理论基本完成止 , 整整经历了20多个世纪 。 从“无理数”这3个字的含义 , 就足以表明人类接受这一概念的艰辛 。
正当人们依旧困惑于负数和无理数的时候 , 又一种披着极为神秘面纱的新数 , 闯进了数学领地 。
平方等于-1的复数i的诞生
1484年 , 法国数学家N.许凯(N.Chuquet , 1445—1500)在一本书中 , 把方程4+x2=3x的根写为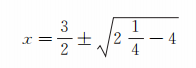
本文图片
尽管他一再声明这根是不可能的 , 但毕竟是第一次形式上出现了负数的平方根 。 这种情形对于今天的初中学生 , 依然是一个望而生畏的禁区 。
1545年 , 意大利数学家卡尔达诺在讨论是否有可能将10分为两个部分 , 而使两者之积等于40时 , 他指出 , 尽管这个问题没有实数解 , 然而 , 假如把答案写成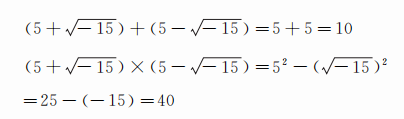
本文图片
虽然卡尔达诺本人怀疑这一运算的合理性 , 但他终究是第一个认真对待数学领地这一不速之客的勇士 。
卡尔达诺之后 , 数学家们接触这种“虚幻”的数越来越多 。 大约100年之后 , 1637年 , 笛卡儿在他的《几何学》一书中 , 给负数的平方根起了一个“虚数”的名 。
本文图片
勒内·笛卡儿
又大约过了140年 , 大数学家欧拉开始用i(imaginary虚幻)表示
1801年 , 高斯系统地使用了符号i , 并把它与实数的混合物a+bi(a、b为实数)称为复数 。 此后i与复数便渐渐通行于全世界 。
起初虚数总给人以一种虚无缥缈的神秘感 , 因为在数轴上找不到它的位置 。 富有想象力的英国牛津大学教授约翰·沃利斯(John Wallis) , 给虚数找到了一个绝妙的解释: 假定某人欠地10亩 , 即他有-10亩地 , 而这-10亩地又恰好是个正方形 , 那么它的边长不就是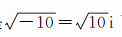
本文图片
了吗?大胆揭开虚数神秘面纱的 , 是挪威测量学家韦塞尔(Wessel , 1745—1818) , 他找到了复数的几何表示法 。
按韦塞尔的解析 , 一个复数如4+3i , 可以如下图那样表示出来 , 其中4是水平方向的坐标 , 3是垂直方向的坐标 。 实数对应于横轴上的点 , 纯虚数对应于纵轴上的点 。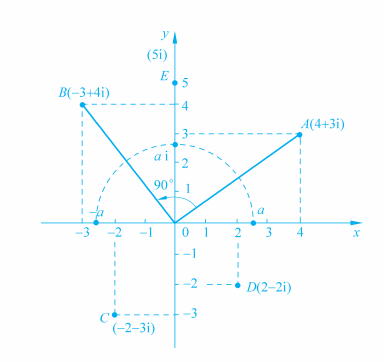
本文图片
一个位于横轴上的实数a , 当它乘以i时变成位于纵轴上的纯虚数ai 。 在几何上这相当于绕原点沿逆时针方向旋转90° 。
如果把ai再乘i , 即又沿逆时针方向转90° , 此时理应转回到横轴负向 , 这一点在下式中表示得更为明显: 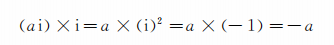
本文图片
有趣的是 , 一个数乘i , 相当于绕原点沿逆时针方向转90° , 这一规律 , 适用于所有的复数 。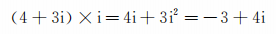
本文图片
由于A、B分别对应于复数4+3i和-3+4i , 从而∠AOB=90° 。
复数在荒岛寻宝上的应用
下面是一则扣人心弦的荒岛寻宝的故事 , 读完之后读者将会看到 , 一旦复数在几何上有了立足点 , 它将是多么有用 。
从前 , 有个年轻人在曾祖父的遗物中偶然发现一张羊皮纸 , 纸上指明了一座宝藏 , 羊皮纸内容是这样的:
“乘船到北纬×× , 西经×× , 即可找到一座荒岛 。 岛的北岸有一大片草地 。 草地上有一棵橡树和一棵松树 , 还有一座绞架 , 那是我们过去用来吊死叛变者的 。 从绞架走到橡树 , 并记住走了多少步; 到了橡树向右拐个直角再走同样步数 , 在这里打个桩 。 然后回到绞架那里 , 再朝松树走去 , 同时记住所走的步数; 到了松树向左拐个直角再走这么多步 , 在那里也打个桩 , 在两个桩的正中挖掘 , 就可以得到宝藏 。 ”
【复数|为什么要有一个数的平方等于-1?】
本文图片
年轻人欣喜万分 , 决心冒险一试 , 于是急忙租了一条船 , 载着满腔的希望驶到了荒岛 。 上岛之后我们年轻的冒险家立时陷入绝望之中 。 他虽然找到了橡树和松树 , 但绞架却不见了!长时间的雨淋日晒 , 绞架已经腐烂成土 , 一切痕迹都已不复存在 。 年轻人气恼地在岛上狂掘一阵 , 然而一切均属徒劳 , 终于两手空空 , 扫兴而归 。
这是一个令人伤心的故事 。 因为 , 如果这个年轻人懂得一点数学 , 特别是虚数的话 , 他本来是有可能找到宝藏的!下面我们来帮帮这个可怜的年轻人 , 尽管此时此刻对于他已经为时太晚 。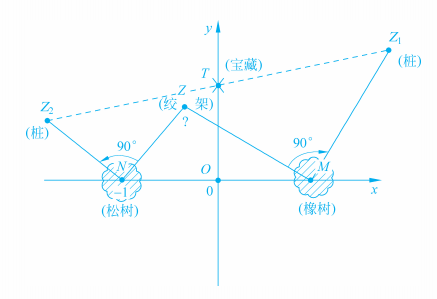
本文图片
如上图所示 , 把荒岛看成一个复数平面 , 以两棵树所在的直线为实轴 。 过两树中点O , 作与实轴垂直的直线OY为虚轴 , 而且以两树M、N之间距离的一半为长度单位 。 这样橡树M和松树N则分别位于实轴的+1与-1点 。
假设未知的绞架位置在Z点处 , 相应的复数为
Z=a+bi
既然绞架在Z点 , 松树N在-1点 , 则两者相对的方位便是Z-(-1)=Z+1 。 把这个数乘以i , 就得到桩Z2的复数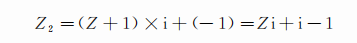
本文图片
同理可得桩Z1的复数(右拐90°相当于乘以-i): 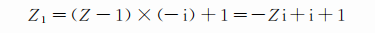
本文图片
宝藏在两根桩的正中 , 因此它所在位置的复数T为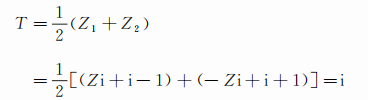
本文图片
这就是说 , 不管绞架位于何处 , 宝藏总在虚轴上相应于复数i的那一点 。 读者若不信 , 可以自己拿张纸 , 变换几个绞架的位置 , 试试看会有什么结果 。
荒岛寻宝的故事已经结束 , 尽管故事中的情节可能是虚构的 , 但沿着-1平方根建立起来的复数体系 , 的确帮助人们在数学和其他科学领域中 , 找到一个又一个的宝藏 。
来源:《给孩子的数学故事书》
作者:张远南 张昶
编辑:张润昕
_原题_:数学|为什么一定要有一个数的平方等于-1?
来源:原点阅读
编辑:谦
推荐阅读
- IT|为什么感染飙升但死亡人数有限?研究显示T细胞可防止奥密克戎引发重症
- 德尔塔|为什么感染飙升但死亡人数有限?研究显示T细胞可防止奥密克戎引发重症
- 车型|买车一定要有OTA?别克来告诉你答案
- 生活|2022,你为什么需要一块华为 WATCH GT3?
- 最新消息|浙江规定明年3月1日起外卖必须要有外卖封签
- 记忆|为什么现在的年度听歌报告,越来越好哭了?
- 符合中国|为什么要注册中文域名?中文域名很好?
- 周建明|周建明:我们为什么要强调基础科学研究?
- 智电|你的纯电MPV,为什么需要一个专业户来操刀?
- 安全|为什么我们现在不再需要杀毒软件了?







