原文链接：http://tecdat.cn/?p=21757
时间序列模型根据研究对象是否随机分为确定性模型和随机性模型两大类 。
随机时间序列模型即是指仅用它的过去值及随机扰动项所建立起来的模型,建立具体的模型,需解决如下三个问题模型的具体形式、时序变量的滞后期以及随机扰动项的结构 。


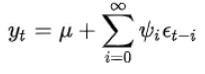
文章图片

μ是yt的均值；ψ是系数 ， 决定了时间序列的线性动态结构 ， 也被称为权重 ， 其中ψ0=1；{εt}为高斯白噪声序列 ， 它表示时间序列{yt}在t时刻出现了新的信息 ， 所以εt称为时刻t的innovation（新信息）或shock（扰动） 。
单位根测试是平稳性检验的特殊方法 。 单位根检验是对时间序列建立ARMA模型、ARIMA模型、变量间的协整分析、因果关系检验等的基础 。
对于单位根测试 ， 为了说明这些测试的实现 ， 考虑以下系列

1. > plot(X,type="l")

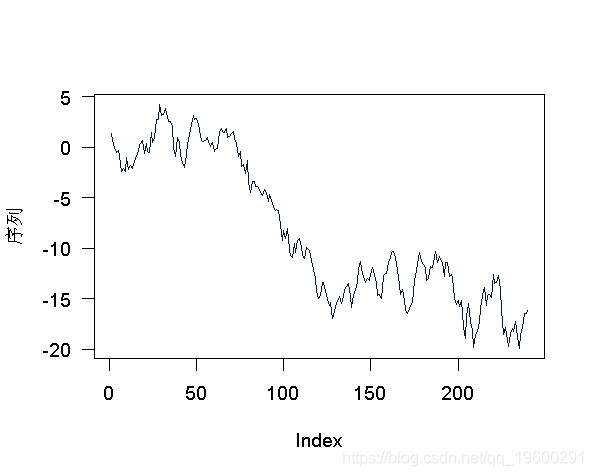
文章图片

• Dickey Fuller（标准）

这里 ， 对于Dickey-Fuller测试的简单版本 ， 我们假设


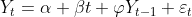
文章图片

我们想测试是否（或不是） 。 我们可以将以前的表示写为


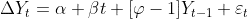
文章图片

所以我们只需测试线性回归中的回归系数是否为空 。 这可以通过学生t检验来完成 。 如果我们考虑前面的模型没有线性漂移 ， 我们必须考虑下面的回归

1. Call:
2. lm(formula = z.diff ~ 0 + z.lag.1)
3. Residuals:
4. Min 1Q Median 3Q Max
5. -2.84466 -0.55723 -0.00494 0.63816 2.54352
6. Coefficients:
7. Estimate Std. Error t value Pr(>|t|)
8. z.lag.1 -0.005609 0.007319 -0.766 0.444
9. Residual standard error: 0.963 on 238 degrees of freedom
10. Multiple R-squared: 0.002461, Adjusted R-squared: -0.00173
11. F-statistic: 0.5873 on 1 and 238 DF, p-value: 0.4442

我们的测试程序将基于学生t检验的值 ，

1. > summary(lm(z.diff~0+z.lag.1 ))$coefficients[1,3]
2. [1] -0.7663308

这正是计算使用的值

1. ur.df(X,type="none",lags=0)
2. ###############################################################
3. # Augmented Dickey-Fuller Test Unit Root / Cointegration Test #
4. ###############################################################
5. The value of the test statistic is: -0.7663

可以使用临界值（99%、95%、90%）来解释该值

1. > qnorm(c(.01,.05,.1)/2)
2. [1] -2.575829 -1.959964 -1.644854

如果统计量超过这些值 ， 那么序列就不是平稳的 ， 因为我们不能拒绝这样的假设 。 所以我们可以得出结论 ， 有一个单位根 。 实际上 ， 这些临界值是通过

1. ###############################################
2. # Augmented Dickey-Fuller Test Unit Root Test #
3. ###############################################
4. Test regression none
5. Call:
6. lm(formula = z.diff ~ z.lag.1 - 1)
7. Residuals:
8. Min 1Q Median 3Q Max
9. -2.84466 -0.55723 -0.00494 0.63816 2.54352
10. Coefficients:
11. Estimate Std. Error t value Pr(>|t|)
12. z.lag.1 -0.005609 0.007319 -0.766 0.444
13. Residual standard error: 0.963 on 238 degrees of freedom
14. Multiple R-squared: 0.002461, Adjusted R-squared: -0.00173
15. F-statistic: 0.5873 on 1 and 238 DF, p-value: 0.4442
16. Value of test-statistic is: -0.7663
17. Critical values for test statistics:
18. 1pct 5pct 10pct
19. tau1 -2.58 -1.95 -1.62

R有几个包可以用于单位根测试 。

1. Augmented Dickey-Fuller Test
2. data: X
3. Dickey-Fuller = -2.0433, Lag order = 0, p-value = https://www.sohu.com/a/0.5576
4. alternative hypothesis: stationary

这里还有一个检验零假设是存在单位根 。 但是p值是完全不同的 。

1. p.value
2. [1] 0.4423705
3. testreg$coefficients[4]
4. [1] 0.4442389

• 增广Dickey-Fuller检验

回归中可能有一些滞后现象 。 例如 ， 我们可以考虑


文章图片

同样 ， 我们需要检查一个系数是否为零 。 这可以用学生t检验来做 。

1. > summary(lm(z.diff~0+z.lag.1+z.diff.lag ))
2. Call:
3. lm(formula = z.diff ~ 0 + z.lag.1 + z.diff.lag)
4. Residuals:
5. Min 1Q Median 3Q Max
6. -2.87492 -0.53977 -0.00688 0.64481 2.47556
7. Coefficients:
8. Estimate Std. Error t value Pr(>|t|)
9. z.lag.1 -0.005394 0.007361 -0.733 0.464
10. z.diff.lag -0.028972 0.065113 -0.445 0.657
11. Residual standard error: 0.9666 on 236 degrees of freedom
12. Multiple R-squared: 0.003292, Adjusted R-squared: -0.005155
13. F-statistic: 0.3898 on 2 and 236 DF, p-value: 0.6777
14. coefficients[1,3]
15. [1] -0.7328138

该值是使用

1. > df=ur.df(X,type="none",lags=1)
2. ###############################################
3. # Augmented Dickey-Fuller Test Unit Root Test #
4. ###############################################
5. Test regression none
6. Call:
7. lm(formula = z.diff ~ z.lag.1 - 1 + z.diff.lag)
8. Residuals:
9. Min 1Q Median 3Q Max
10. -2.87492 -0.53977 -0.00688 0.64481 2.47556
11. Coefficients:
12. Estimate Std. Error t value Pr(>|t|)
13. z.lag.1 -0.005394 0.007361 -0.733 0.464
14. z.diff.lag -0.028972 0.065113 -0.445 0.657
15. Residual standard error: 0.9666 on 236 degrees of freedom
16. Multiple R-squared: 0.003292, Adjusted R-squared: -0.005155
17. F-statistic: 0.3898 on 2 and 236 DF, p-value: 0.6777
18. Value of test-statistic is: -0.7328
19. Critical values for test statistics:
20. 1pct 5pct 10pct
21. tau1 -2.58 -1.95 -1.62

同样 ， 也可以使用其他包：

1. Augmented Dickey-Fuller Test
2. data: X
3. Dickey-Fuller = -1.9828, Lag order = 1, p-value = https://www.sohu.com/a/0.5831
4. alternative hypothesis: stationary

结论是一样的（我们应该拒绝序列是平稳的假设） 。

• 带趋势和漂移的增广Dickey-Fuller检验

到目前为止 ， 我们的模型中还没有包括漂移 。 但很简单（这将被称为前一过程的扩充版本）：我们只需要在回归中包含一个常数 ，

1. > summary(lm)
2. Residuals:
3. Min 1Q Median 3Q Max
4. -2.91930 -0.56731 -0.00548 0.62932 2.45178
5. Coefficients:
6. Estimate Std. Error t value Pr(>|t|)
7. (Intercept) 0.29175 0.13153 2.218 0.0275 *
8. z.lag.1 -0.03559 0.01545 -2.304 0.0221 *
9. z.diff.lag -0.01976 0.06471 -0.305 0.7603
10. ---
11. Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
12. Residual standard error: 0.9586 on 235 degrees of freedom
13. Multiple R-squared: 0.02313, Adjusted R-squared: 0.01482
14. F-statistic: 2.782 on 2 and 235 DF, p-value: 0.06393

考虑到方差输出的一些分析 ， 这里获得了感兴趣的统计数据 ， 其中该模型与没有集成部分的模型进行了比较 ， 以及漂移 ，

1. > summary(lmcoefficients[2,3]
2. [1] -2.303948
3. > anova(lm$F[2]
4. [1] 2.732912

这两个值也是通过

1. ur.df(X,type="drift",lags=1)
2. ###############################################
3. # Augmented Dickey-Fuller Test Unit Root Test #
4. ###############################################
5. Test regression drift
6. Residuals:
7. Min 1Q Median 3Q Max
8. -2.91930 -0.56731 -0.00548 0.62932 2.45178
9. Coefficients:
10. Estimate Std. Error t value Pr(>|t|)
11. (Intercept) 0.29175 0.13153 2.218 0.0275 *
12. z.lag.1 -0.03559 0.01545 -2.304 0.0221 *
13. z.diff.lag -0.01976 0.06471 -0.305 0.7603
14. ---
15. Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
16. Residual standard error: 0.9586 on 235 degrees of freedom
17. Multiple R-squared: 0.02313, Adjusted R-squared: 0.01482
18. F-statistic: 2.782 on 2 and 235 DF, p-value: 0.06393
19. Value of test-statistic is: -2.3039 2.7329
20. Critical values for test statistics:
21. 1pct 5pct 10pct
22. tau2 -3.46 -2.88 -2.57
23. phi1 6.52 4.63 3.81

我们还可以包括一个线性趋势 ，

1. > temps=(lags+1):n
2. lm(z.diff~1+temps+z.lag.1+z.diff.lag )
3. Residuals:
4. Min 1Q Median 3Q Max
5. -2.87727 -0.58802 -0.00175 0.60359 2.47789
6. Coefficients:
7. Estimate Std. Error t value Pr(>|t|)
8. (Intercept) 0.3227245 0.1502083 2.149 0.0327 *
9. temps -0.0004194 0.0009767 -0.429 0.6680
10. z.lag.1 -0.0329780 0.0166319 -1.983 0.0486 *
11. z.diff.lag -0.0230547 0.0652767 -0.353 0.7243
12. ---
13. Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
14. Residual standard error: 0.9603 on 234 degrees of freedom
15. Multiple R-squared: 0.0239, Adjusted R-squared: 0.01139
16. F-statistic: 1.91 on 3 and 234 DF, p-value: 0.1287
17. > summary(lmcoefficients[3,3]
18. [1] -1.98282
19. > anova(lm$F[2]
20. [1] 2.737086

而R函数返回

1. ur.df(X,type="trend",lags=1)
2. ###############################################
3. # Augmented Dickey-Fuller Test Unit Root Test #
4. ###############################################
5. Test regression trend
6. Residuals:
7. Min 1Q Median 3Q Max
8. -2.87727 -0.58802 -0.00175 0.60359 2.47789
9. Coefficients:
10. Estimate Std. Error t value Pr(>|t|)
11. (Intercept) 0.3227245 0.1502083 2.149 0.0327 *
12. z.lag.1 -0.0329780 0.0166319 -1.983 0.0486 *
13. tt -0.0004194 0.0009767 -0.429 0.6680
14. z.diff.lag -0.0230547 0.0652767 -0.353 0.7243
15. ---
16. Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
17. Residual standard error: 0.9603 on 234 degrees of freedom
18. Multiple R-squared: 0.0239, Adjusted R-squared: 0.01139
19. F-statistic: 1.91 on 3 and 234 DF, p-value: 0.1287
20. Value of test-statistic is: -1.9828 1.8771 2.7371
21. Critical values for test statistics:
22. 1pct 5pct 10pct
23. tau3 -3.99 -3.43 -3.13
24. phi2 6.22 4.75 4.07
25. phi3 8.43 6.49 5.47

• KPSS 检验

在这里 ， 在KPSS过程中 ， 可以考虑两种模型：漂移模型或线性趋势模型 。 在这里 ， 零假设是序列是平稳的 。
代码是

1. ur.kpss(X,type="mu")
2. #######################
3. # KPSS Unit Root Test #
4. #######################
5. Test is of type: mu with 4 lags.
6. Value of test-statistic is: 0.972
7. Critical value for a significance level of:
8. 10pct 5pct 2.5pct 1pct
9. critical values 0.347 0.463 0.574 0.73

在这种情况下 ， 有一种趋势

1. ur.kpss(X,type="tau")
2. #######################
3. # KPSS Unit Root Test #
4. #######################
5. Test is of type: tau with 4 lags.
6. Value of test-statistic is: 0.5057
7. Critical value for a significance level of:
8. 10pct 5pct 2.5pct 1pct
9. critical values 0.119 0.146 0.176 0.216

再一次 ， 可以使用另一个包来获得相同的检验（但同样 ， 不同的输出）

1. KPSS Test for Level Stationarity
2. data: X
3. KPSS Level = 1.1997, Truncation lag parameter = 3, p-value = https://www.sohu.com/a/0.01
4. > kpss.test(X,"Trend")
5. KPSS Test for Trend Stationarity
6. data: X
7. KPSS Trend = 0.6234, Truncation lag parameter = 3, p-value = https://www.sohu.com/a/0.01

至少有一致性 ， 因为我们一直拒绝假设 。

• Philipps-Perron 检验

Philipps-Perron检验基于ADF过程 。 代码

1. > PP.test(X)
2. Phillips-Perron Unit Root Test
3. data: X
4. Dickey-Fuller = -2.0116, Truncation lag parameter = 4, p-value = https://www.sohu.com/a/0.571

另一种可能的替代方案是

1. > pp.test(X)
2. Phillips-Perron Unit Root Test
3. data: X
4. Dickey-Fuller Z(alpha) = -7.7345, Truncation lag parameter = 4, p-value
5. = 0.6757
6. alternative hypothesis: stationary

• 比较

我不会花更多的时间比较不同的代码 ， 在R中 ， 运行这些测试 。 我们再花点时间快速比较一下这三种方法 。 让我们生成一些或多或少具有自相关的自回归过程 ， 以及一些随机游走 ， 让我们看看这些检验是如何执行的：

1. > for(i in 1:(length(AR)+1)
2. + for(s in 1:1000){
3. + if(i!=1) X=arima.sim
4. + M2[s,i]=(pp.testp.value)
5. + M1[s,i]=(kpss.testp.value)
6. + M3[s,i]=(adf.testp.value)
7. + }

这里 ， 我们要计算检验的p值超过5%的次数 ，

1. > plot(AR,P[1,],type="l",col="red",ylim=c(0,1)
2. > lines(AR,P[2,],type="l",col="blue")
3. > lines(AR,P[3,],type="l",col="green")

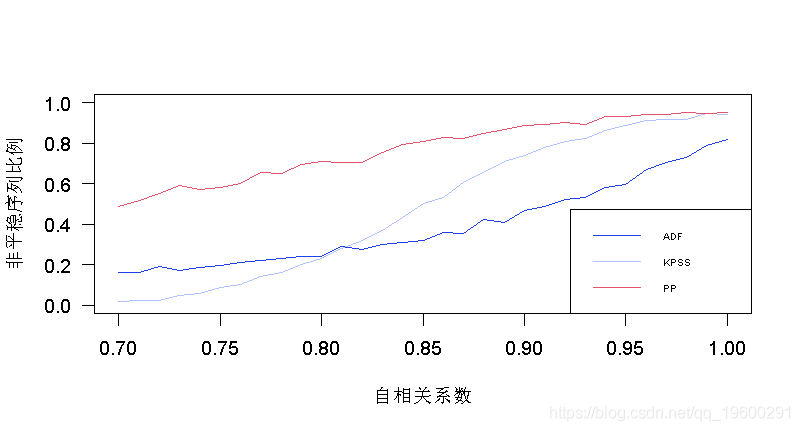
文章图片

我们可以在这里看到Dickey-Fuller测试的表现有多不稳定 ， 因为我们的自回归过程中有50%(至少)被认为是非平稳的 。


文章图片

最受欢迎的见解
1.Matlab马尔可夫链蒙特卡罗法（MCMC）估计随机波动率（SV ， Stochastic Volatility） 模型
2.基于R语言的疾病制图中自适应核密度估计的阈值选择方法
3.WinBUGS对多元随机波动率模型：贝叶斯估计与模型比较
4.R语言回归中的hosmer-lemeshow拟合优度检验
5.matlab实现MCMC的马尔可夫切换ARMA – GARCH模型估计
6.R语言区间数据回归分析
7.R语言WALD检验 VS 似然比检验
8.python用线性回归预测股票价格
【语言|拓端tecdat|R语言时间序列平稳性几种单位根检验（ADF，KPSS，PP）及比较分析】9.R语言如何在生存分析与Cox回归中计算IDI ， NRI指标

推荐阅读

• 

  孕妇能吃板栗吗 孕妇吃板栗的好处
• 

  胎菊喝多了有什么害处
• 

  大球盖菇种植技术 大球盖菇种植技术与管理
• 

  科目三挂了重新预约考试要等多久
• 

  高铁票如何改签
• 

  多大年龄办理社保合适 办理社保讲解
• 

  凯越变速箱油尺怎么看
• 

  海盐抹脸部的正确方法 海盐怎么抹脸部
• 

  这是啥鱼不是鲤鱼，没见过这种颜色的鱼
• 

  活动策划的5大方面 线下活动策划方案内容
• 

  拜托了咖啡结局
• 

  1000gb等于多少t
• 

  灵异故事 东大软件园的同心湖
• 

  7种自制补水面膜 让爱美女性肌肤富有弹性光泽
• 

  伊索寓言是一部什么故事集 伊索寓言收录什么故事
• 

  女生一个人在外地生活需要注意些啥有没有啥提高生活质量的小习惯
• 

  小额贷款太多房贷被拒绝怎么补救
• 

  冬笋焯水有点苦怎么办 如何解决冬笋焯水有点苦
• 

  重庆大学的王牌专业排名，重庆大学最好的专业是什么
• 

  梦幻西游一个175带小号可以遇到持国嘛 梦幻西游如何快速抓持国

• Linux|Fedora 36默认字体将改为Noto，以覆盖更多语言
• 人物|日本高中生开发创意“语言计算器”获大奖 突破1+1=2模式
• 语法|?沈家煊《从语言看中西方的范畴观》
• 功能|谷歌正开发Panlingual功能：Android 13支持为单个App指定语言
• Google|Android 13正开发Panlingual功能：可为单个App指定语言
• Google|Android 13正开发Panlingual功能：为APP指定语言
• 模式|考那么多试，拿那么高分，大模型们真的懂语言了吗？
• 网络|为什么要拒绝低俗网络用语
• 研究成果|本世纪末1500种语言或不再使用
• 语言|本世纪末1500种语言或不再使用