
文章图片
【熵的概念的发展:麦克斯韦妖与信息】
文章图片
在所有物理学中 , 熵是最独特但最神秘的概念之一 。 普遍的解释是 , 它是宇宙无序的量度 , 热力学第二定律指出熵永远不会减少 。 换句话说 , 宇宙正朝着越来越无序的方向发展 。 一些科学家认为 , 正是熵的这种单向特性 , 造成了时间也单向流动 。
物理学家麦克斯韦提出了一个名为麦克斯韦妖的思想实验 , 该实验展示了一种可以逆转封闭系统熵的机制 , 这将违反热力学第二定律 。 100多年来没有人能够解决这个悖论 , 但是当IBM的计算机研究人员最终解决了这个悖论时 , 他们发现熵与更基本的东西有关 , 那就是信息 。
熵和信息之间有什么联系?这就是我们今天所要探讨的 。
熵的定义如果我们观看行星绕太阳的旋转视频 , 然后将视频倒放 , 那么反转的运动并没有什么异常 , 这在物理定律范围内是允许的 。 据我们所知 , 大部分物理定律都是时间可逆的 。 唯一看似时间不可逆的物理定律是熵增定律 , 也就是热力学第二定律 。 打破鸡蛋是一个很好的例子 , 如果在视频中看到鸡蛋自动复原 , 我们就会知道它是倒放的 , 因为这个过程的熵是减少的 , 违反了热力学第二定律 。
热力学第二定律指出 , 在孤立系统中 , 熵永远不会减少 。 但这并没有告诉我们熵是什么 , 所以熵是如何定义的?常见的定义是熵是系统混乱度的量度 , 但这并不是很精确 。 为了更好地理解熵 , 让我们看一个简单的例子 。
气体被屏障隔离在一个容器的左半边 , 如果我们移除屏障 , 那么气体将会膨胀到容器的全部体积 , 在这个过程中气体的熵增加了 。 我们不禁会问 , 为什么气体膨胀到全部体积 , 混乱程度会增加?原因是体积更大 , 单个气体分子可能存在的位置更多 , 因此可能的排列方式会更多 。
这种更大的可能排列数量确实是对熵的更好描述 , 玻尔兹曼首先提出了这一见解作为熵的另一种定义 , 它是一种计算系统内原子排列数量的方法 。 现在如果我们在右壁上有一个柱塞 , 并将气体推回到原来的位置 , 这会使气体的熵降低吗?很显然也是不会的 , 做功会使气体温度升高 , 温度与原子速度相关 , 使描述原子运动方式的数量增加 。
还有一个问题 , 气体是否会自发排列 , 使其仅填充容器一半的体积 。 我们可能会说这是不可能的 , 因为它会通过减少熵来违反第二定律 。 是的 , 它会违反第二定律 , 但事实是物理定律中没有任何东西可以真正阻止这种情况的发生 , 除非它的可能性非常低 。 气体中有数万亿个分子自发排列在容器一侧的概率大约是10^-15(后面还有21个0) , 这个数字是如此之小 , 以至于在统计上是不可能的 。
麦克斯韦妖与信息所以上面的例子告诉我们第二定律不会很快被违反 , 但它也告诉我们第二定律不是绝对定律 , 是一个统计定律 。 换句话说 , 它可能会被违反 , 但极不可能被违反 。
1867年 , 物理学家麦克斯韦设计了一个思想实验 , 表明第二定律可能被违反 , 熵确实可以减少 。 这个思想实验对科学家来说似乎完全合理 , 他们在100多年里都无法找出它错在哪里 。 开尔文后来将这个思想实验称为麦克斯韦妖 。
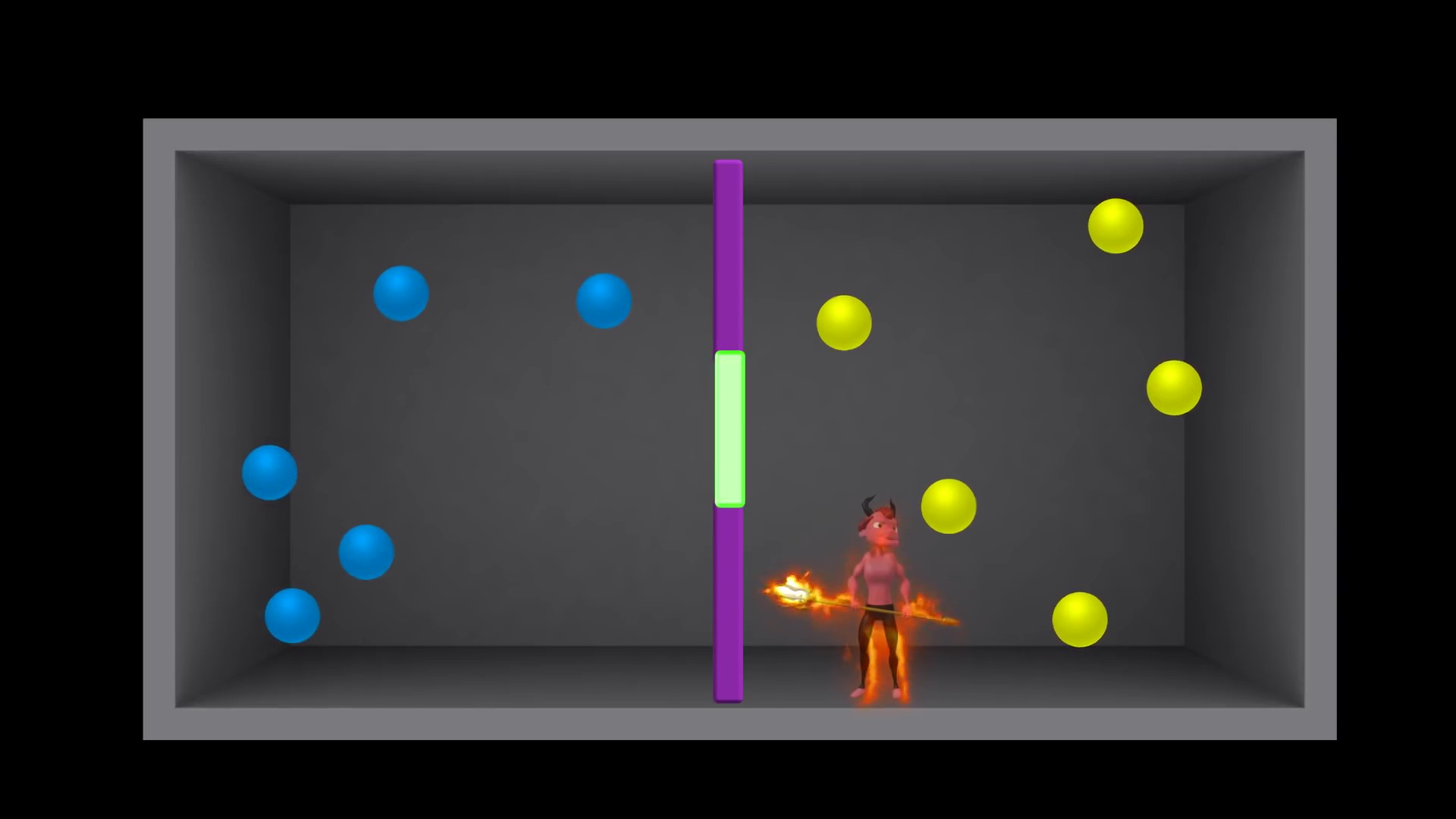
想象以下场景 , 一个容器中间有一个隔板 , 隔板的一侧充满气体 , 另一侧则是真空 。 这个隔板留有一个小门 , 那扇门是无摩擦的 , 所以不会向封闭系统增加热量 , 并且这个小门的开关由一个小妖怪控制 。 气体分子有运动速度快和慢两种情况 , 这个小妖怪控制门的开关每次只让一个速度快的分子通过 。 最终容器一边是冷的气体 , 另一边是热的气体 , 可以利用此温差驱动热机作用 , 显然违反了第二定律 。
解决方案终于在1982年由IBM研究中心的两位科学家提出 , 他们将妖的想法归结为熵背后更基本的概念 , 那就是信息 。 为了让妖减少熵 , 他必须收集有关各种分子运动的信息 , 以确定何时打开和关闭门 。 妖正在增加系统中的信息量 , 因为他是系统的一部分 。 这种信息的增加是熵的增加 , 他们表明气体较少的熵正好被妖大脑中信息的增加所抵消 , 所以没有违反第二定律 。
推荐阅读
- 宇宙真的存在大过滤器?费米悖论的最终解释,人类可能真是孤独的!
- 钻入南极冰下800米,发现大量古生物群,改变了人类对生命的认知
- 人类还在进化吗?别着急下定论,你的身体正在告诉你答案
- 坚持少睡能让大脑更聪明?科学研究认为,睡太久会损伤脑细胞皮层
- 欧洲虎鲸频繁攻击船的方向舵,却从不伤人,科学家:只是因为好玩
- 太岁究竟是什么“东西”?我国科学家用精密仪器检测揭示太岁之谜
- 科学家发现超光速方法,将人类极限速度提升1000倍以上,可能吗?
- 神农架重现已灭绝50万年生物,地球自我修复?还是玛雅预言成真?
- 现存最大的猛禽,翼展达3米以上,能飞172公里远5小时不扇翅膀



