文章图片
文章图片

文章图片

不仅知道地球是圆的 , 2200多年前 , 他还用简单数学算出了地球周长 。
太不可思议了!
【2000多年前此人就算出了地球周长!地球是圆的原来古人早就知道】前几天我们刚刚经历了夏至 , “至”不是到来的意思 , 而是代表极至;这一天是一年之中 , 太阳与地面垂直的最北之处(也就是北回归线) , 再来太阳就又慢慢南移了 。 因此夏至是北半球整年度白昼最长的日子 , 而位于北回归线的物体到了正午时刻 , 就会没有影子 。
而2200多年前的一个夏至 , 古希腊的埃拉托斯塞尼就利用这点计算出了地球的周长 。
埃拉托斯塞尼的出生地在现今的利比亚地区 , 他长大后到雅典接受教育 , 精通数学、天文学、地理学 , 还是位诗人 。 西元前245年 , 他被托勒密国王任命为当时世界上最大的亚历山大图书馆馆长 , 约五年后 , 他想到了测量地球大小的方法 。
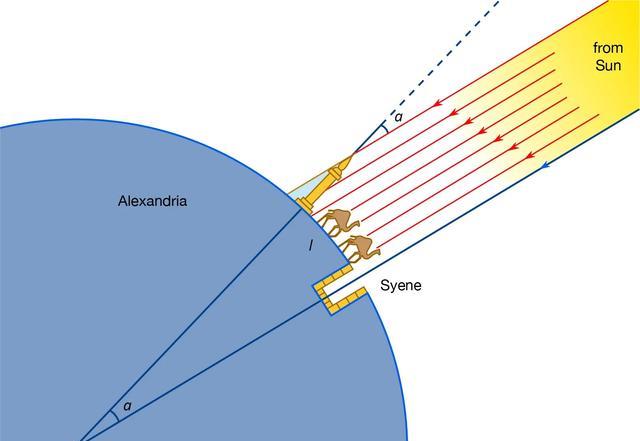
埃拉托斯塞尼从文献记载得知 , 位于亚历山大南方的塞耶尼有一口水井 , 每年的夏至正午 , 水井深处的水面正好映照出完整的太阳 , 也就是说太阳此刻恰好与地面垂直 。
夏至的正午在亚历山卓的物体还是有影子的 , 代表阳光是斜射过来的 , 与物体的顶端有个夹角 。 假设射到地球的太阳光线是平行的 , 而地球正圆形 , 那么这个夹角就会等于亚历山大图书馆到塞耶尼这段圆弧对应到地心的圆心角;只要知道角度多少 , 就能从两地距离依比例推算出地球的周长 。
埃拉托斯塞尼测出夹角是7.2度 , 代表圆心角相当于360度的1/50;而塞耶尼距离亚历山大5000“斯塔德”(stadia , 古希腊距离单位) , 因此地球周长等于25万斯塔德 。 (后来埃拉托斯塞尼又把地球周长调整成25万2千斯塔德 , 或许是因为这个数目被10以内的自然数都能整除)
斯塔德在不同地区所定义的长度各不相同 , 若按托勒密王国的一般标准相当于185公尺 , 但也有学者将当时测量的距离与现今比较 , 换算出来的是157.7公尺 。 若是前者 , 25万斯塔德相当于4万6千公里;后者则是3万9千公里 , 与实际地球周长四万公里误差只有2.5% 。
就算是拿4万6千公里这个数字来比较 , 误差15%就高了点 , 但这仍无碍于埃拉托斯塞尼所展现的高超抽象思考能力 。 以当时的技术 , 绝对不可能实际测量出地球周长(更不用说大部分人仍认为地球是平的) , 但他却能将自然现象化约为简洁的几何模型 , 不用蛮力 , 也无需深奥的理论 , 就解开这看似无解的问题 , 堪称是最能呈现科学之力与美的代表作之一 。
但是 。。。。 埃拉托斯塞尼是怎么量出7.2度的?
试想一下 , 假如夏至这天你想效法埃拉托斯塞尼算出地球周长 。 带着竿子在北回归线处 , 顶着烈阳等正午时刻一到 , 开始进行测量 。
可问题来了 , 原来竿子的黑影并没有截然分明的边界 , 因此该如何认定影子的长度就一定会产生误差 。 当然 , 竿子如果越长 , 误差比例就越小 , 所以在某些故事版本里 , 埃拉托斯塞尼并不是用竿子 , 而是测量方尖碑的影子 , 感觉上似乎比较有道理 。
但是 , 已知直角三角形的底(影子)跟高(竿子或方尖碑)就能反推出斜边与高的夹角 , 这三角几何是埃拉托斯塞尼死后才出生的希帕克斯发明的 , 所以也不可能用这个方法算出 。
《如何帮地球量体重》这本书的作者认为他是用希腊时期常见的一种碗型日晷算出的 。 晷针的影子比较清楚 , 然后埃拉托斯塞尼只要测量弧型影子的长度 , 以及碗的完整圆周周长 , 就可算出影子是圆周的1/50 , 而不用知道角度 。 不过这个前提是碗型日晷要做得很浑圆 , 否则误差也会很大 , 我们不确定当时是否有这样的技术能力 。
比较可能的应该还是要测量夹角 。 怎么测呢?我想像的是从影子末端拉一根细线到晷针顶端 , 然后拿块绷平的薄纱 , 描绘出晷针与细线 , 就可量测出夹角占全圆的比例 。 当时还没有量角器 , 比较简单的方式可能是:一直将夹角复制贴上 , 最后凑满一个圆刚好是50个 。
推荐阅读
- 在木卫一上看木星有多大?巨物恐惧者慎入,会呼吸不了
- 奥古斯丁“恶”的问题研究:是与生俱来的, 由原生的恶引起的次生的恶
- 木卫一上看木星有多大?巨物恐惧者慎入
- 2022年最震撼大片,必看!
- 东方红卫星已经失联52年,如今现状怎样?中国能否将其带回家?
- 深度科学:人类是整个宇宙中唯一的智能生命的概率是多少?
- 秘鲁发现千年前的线条,使用几何学画出50公里图案,须用卫星观测
- 人类可以飞出地球, 为何不能钻透地球? 现在就来告诉你答案
- 世界号发射成功,首次挑战“一箭多星”,下一步月球火星空间站?