起诉对称
对称无形对称玄
尘埃寰宇亦承传
左冲右突难磁电
不忍分离写素笺
1. 引子
要不要像 Ising 老师那样 , 开头也来一首诗?好吧!我就不装了 , 写不出来 , 还是留给 Ising 老师吧 。 不过 , 倒是可以借用他在《唯像简洁、物格纷繁》中写的:
世人多赞物格闲 , 未晓前程万万难 。
朗道功成凭对称 , 破缺之外更高山 。
来表达我要讲的主题 。
对 , 这里要讲的主题与对称性相关 。 而对称性 , 是一个看着简单、实际却是充满神秘感的“造世主” 。 那些充满中国元素的天地、日月、生死、阴晴、男女等 , 都是它的手笔 。 就连日常生活中 , 它的身影也随处可见 。 也可能只是在学物理的人眼中 , 才随处可见 。 不信?那就给各位来一个真实的八卦:

本文图片
图 1. (a) 玄武湖夜景 (b) 丽达玫瑰
一个学物理的男生和自己的女朋友去到玄武湖 , 看到了夜晚漂亮的灯光 , 如图 1(a) 所示 。 女生忍不住大加赞美:灯火真美 , 有湖水相映衬 , 好有繁华盛世之感 。 不期然 , 男生却来了句:一个镜面对称而已!有点煞风景 , 但还好 。 女生似乎感觉到男生把水面比喻成镜子 , 还算有点浪漫和趣味 。
随后 , 他们在公园里又看到一朵开放得很漂亮的花 , 类似于图 1(b) 所示 。 女生欣喜地说:这花我认识 , 是丽达玫瑰 , 开得好美 。 这时男生也走了过来 , 惊讶地说道:这花开得不物理啊!女生不解地看着男生 , 不懂男生为什么这样说 。 男生只管自顾自地看着花嘀咕道:五重旋转对称 , 自发极化沿着生长方向!但是 , 五重旋转对称不能在晶体中存在…… 。
当然 , 女生像是看“神经病”一般看着男生 , 似乎觉得他魔咒了!男生抬起头 , 看着女生的脸 , 认真地说:那花儿不够对称 , 远不如你的脸长得对称!
女生终于受不了 , 生气地转身就走 。 就这样 , 男生很成功地把自己的女朋友给对称没了 。 可恨的是 , 男生看着女生的背影 , 像是又想到了什么 , 继续说道:相对于我 , 她正在发生一个平移…… 。
这个八卦当然有添油加醋的成分 , 但生活到处都是物理却是我们物理人独有的财富 。 对称性也与我们的生活密切相关 , 例如对称性可以抵抗异性相吸 , 从而推开女友 。
好吧!我承认 , 扯得有点远了 。 这里主要是想给读者一个关于对称性和对称操作的认识 , 正如上面提到的一些概念 , 如“映射”、“镜面”、“旋转对称轴”、“平移”等 。 这里强调一点 , 因为是科普文 , 本文会出现一些非专业术语 , 所以意在表述物理图像 。 读者浏览时大致能够明白要表达的意思就行 。
2. 对称操作
请允许我提及几点与凝聚态物理相关的对称性操作 。 之所以要铺垫这些知识 , 是因为固体物理研究的对象多是晶胞 。 一个三维晶格中的原子 , 总是可以通过平移、旋转、映射、反演 (包括空间和时间反演) 等操作之一个或多个 , 而与其它位置的原子联系 (重叠) 起来 。 正因为对称操作关联着原子的位置 , 分析这种操作 , 对理解铁电极化的来源有重要意义 。 您看 , 直到这里 , 笔者终于说到了和自己相关的物理知识与背景 , 如释重负 。
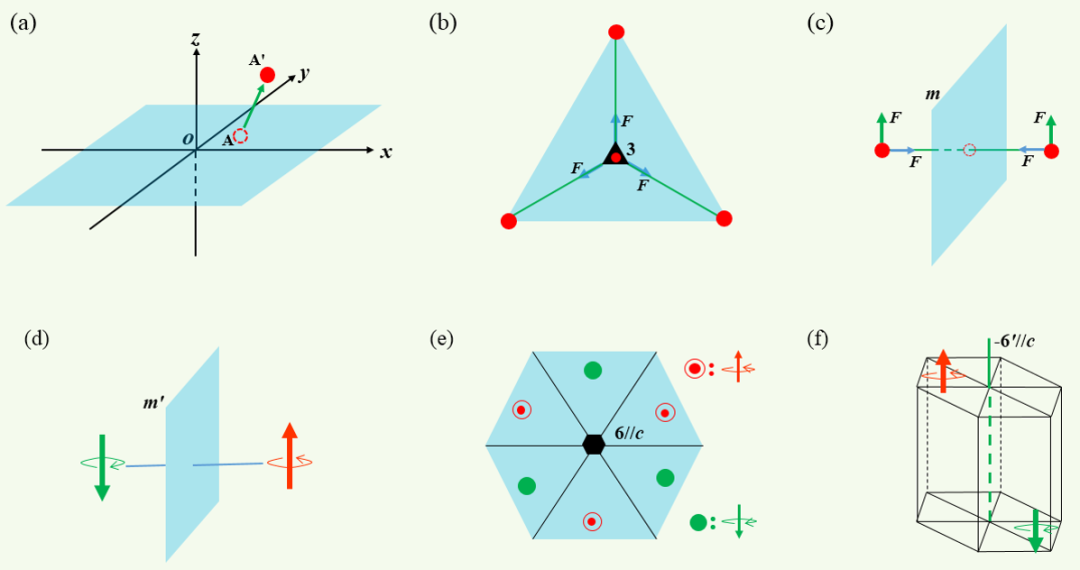
首先 , 平移是比较好理解的一种操作 。 举个例子 , 如图 2(a) 所示:一个原子可沿任意方向运动 , 如由 A 点移动到了 A' 点 。 由于不受任何对称性限制 , 这个“任性”的原子移动会打破中心对称 , 产生铁电极化 。 当然原子位移方向的任意性 , 造就了铁电极化的方向也会不受对称性限制 。 看到这里 , 思想比较活跃的人可能已经想到 , 这种平移操作对应的应该是三斜点群 1(极性方向为 [h k l ]) 。
其次 , 旋转也是我们较多遇到的一种操作 。 我们经常会在文献中看到:某个材料 , 沿着某个方向有几 (2、3、4、6) 重旋转对称轴 , 云里雾里 。 如图 2(b) 展示的 , 是沿 c 方向的三重旋转对称轴 。 这里需要多说一点:沿着旋转轴的方向 , 可以允许有极化产生 , 因为原子沿着旋转轴移动时并不受面内对称性操作的限制 。 但是 , 垂直旋转轴方向就不同 , 由于旋转对称的原因 , 垂直旋转轴的方向之净极化必须为零 。 这一结果应该很好理解 , 因为面内就像有三个呈 120° 大小相等的力 (或者可以想象成库仑力) , 这样就“束缚”了原子在面内乱动 , 面内就不会有净极化产生 。 旋转操作对应着单斜点群中的 2、三方点群中的 3、四方点群的 4 和六方点群的 6 。 这些晶格点群都允许轴向极化 , 并且极性必须平行于旋转轴 , 不能有丝毫差池 。
再次 , 映射 (也就是镜面对称操作) 也比较常见 。 不用多说 , 读者可能已领会到其重要性 , 如图 2(c) 所示 。 考虑两种运动:满足镜面对称的一对原子 , 沿着垂直镜面方向 (法向) 运动 。 对称性要求这对原子只能始终保持反向运动 , 就像一对大小相等方向相反的作用力作用在这两个原子上 。 如此 , 必然导致镜面法线方向净极化为零 。 当这对原子沿平行镜面方向运动时 , 因为对称性要求 , 运动必须始终保持同向 , 就像大小相等方向相同的一对作用力一样 。 很显然 , 这种运动可在平行镜面方向产生极化 。 如此这般的镜面操作 , 对应着点群 m , 极性方向平行镜面方向 , 也不能有任何差错 。
最后 , 是空间反演对称操作 。 这个操作最为简单、直接明了 , 就是不管以上三种啥操作 , 它都给你来一个空间反转 (可以想象三维空间中 , 总有一个反作用力伴随存在) 。 结果就是 , 不管有没有极化都给你转没了 。 也就是说 , 铁电极化都不满足这种空间反演对称性 , 它们不是好东西!与此对应的点群包括三斜 – 1、单斜 2 / m、三方 – 3、四方 – 4、六方 – 6 等 , 都是非极性点群 。
不必多作说明 , 对作铁电材料的人来说 , 这些破群真的是“无敌的对手”或者“天敌” 。
总结一下 , 按照传统的铁电对称性破缺理论 , 极化只会出现在如 1、2 等十个极性点群中 。 这些点群操作下的空间反演对称都破缺了 , 就有可能会有极化产生 , 形成我们所说的铁电体 。
说起来 , 对称性规则施加给铁电体的规范也就这么点东西 。 所以 , 很多人会感觉就这……也没啥啊、原来铁电的图像很直观啊、balabalabala 。 的确 , 在第 II 类多铁性被发现之前 , 就对称性破缺与磁电性质而言 , 磁电的物理图像的确简单明了 。
时光到了 2003 年 。 那时候开始 , 第 II 类多铁性体登堂入室 , 情形就很不同了!
本文图片
图 2. (a) - (c) 分别为平移、旋转、映射对称操作 (d) 映射 + 时间反演对称操作 , 其中红色箭头表示满足右手螺旋向上的自旋、绿色箭头表示满足右手螺旋向下的自旋 (e) 为反铁磁序的六重对称轴 6' (f) 为反铁磁态 + 空间反演对称的六重对称轴 - 6'
3. 多铁性对称操作
既然很不同 , 那就看看铁电材料的“革命家”:第 II 类多铁 (Type - II multiferroics) 中的对称性问题 。 有关第 II 类多铁的科普文章 , 读者可以从很多地方读到 。 比如陈湘明老师和 Ising 老师他们写的综述 , 如《多铁性迷思》、《电控磁性》等 。 这里 , 只重点说明磁电效应与对称性之间的关系 。
特定自旋结构诱导的铁电极化 , 严格而言并不必须仰仗特殊的极性空间群 。 不是极性空间群也能出现铁电极化?这很无厘头 。 但伴随着强的磁电耦合机制出现 , 这类铁电性的物理图像开始备受关注 , 至少从对称性角度看需要重新梳理 。 抛开实验现象不说 , 前面提到的四种对称操作 , 似乎已经不能圆满解释第 II 类多铁中的铁电极化 , 因为铁电极化竟然在空间反演对称的体系中出现了 。 笔者能深深体会到第 II 类多铁给铁电人带来的喜悦 , 因为它把空间反演对称这个“天敌”给干翻了 。
例如 , 人们熟知的第 II 类多铁“开山祖师”级化合物:TbMnO3 , 其晶格结构就属于中心对称的点群 mmm , 对应的空间群为 Pbnm (No. 62) [1] 。 按照之前的理论 , 中心对称的体系不允许有极化 。 但是 , TbMnO3 中形成的特殊自旋序扯破了这个传统的“牢笼” , 人们在实验上观测到了明显的铁电极化 。 如此 , 现在似乎可以不再受制于中心对称空间群的限制 , 就能寻找到更多的铁电体!
但开始行动之前 , 因为牵涉到自旋序 , 所以还需追加一类对称操作概念的描述 , 即给出时间反演对称操作的图像是什么 。
时间反演描绘的是对电子自旋的操作 。 电子自旋可以想象成一个自转的转子 , 因为携带转动过程 , 就必然与时间 t 相联系 , 也即与动量、速度之类的动力学过程相联系 。 因此 , 跟自旋磁性相关的过程 , 其时间反演对称一定是破缺的 。 具体到这里,考虑两种情况:
(1) 映射加时间反演操作 , 如图 2(d) 所示:一对电子 , 从电荷层面看 , 满足镜面对称 , 与时间无关 。 加上对自旋的表述 , 可以用右手螺旋方向的反转来表示时间反演 。 当然 , 理解时间反演图像的时候 , 不同人习惯用的方法不同 , 没有统一规定 。 镜面右侧的电子自旋满足右手螺旋、拇指向上 。 这时若是只考虑镜面对称的话 , 左侧的电子应该是左手螺旋、拇指向上 , 因为镜面对称是手性的,这与图 2(c) 类似 , 不做赘述 。 这里考虑映射对称加时间反演对称两重操作:考虑右侧的电子满足右手螺旋、拇指向上;左侧的电子同样需要满足右手螺旋 , 指向就变成拇指向下了 , 即时间反演对称破缺 。 显然 , 这时的单纯镜面操作 m 被破坏了 , 我们用 m' 来表示 。
(2) 旋转操作 , 如图 2(e):对一个六重旋转对称体系 , 时间反演对称破缺 , 反铁磁态破坏了六重旋转对称操作 6 , 因为此时箭头流动指向反转 。 如此 , 6 重旋转操作 , 加上时间操作 , 对应的点群就变成 6' 。
基于前述之镜面反演操作和旋转操作 , 可以看出 , 当同时考虑时间反演和空间反演操作时 , 若反铁磁破坏时间反演对称操作的同时满足空间反演对称性 , 就可以认为时间反演加空间反演这一联合操作不变 (也就是 CP 反演对称) 。 至于为何联合操作不变?其中缘由和具体物理图像在后面会涉及到 。 但是 , 若反铁磁材料本身就不满足空间反演对称性 (例如上面提到的旋转操作 1、3 等) , 这时所谓的“时间反演加空间反演联合操作不变”也就失去意义了 。 此时空间反演的不对称 , 可能会引起电子云的畸变 , 诱导出弱 canting 型铁磁态 , 展现磁电耦合性质 。 另外 , 对铁磁破坏时间反演操作的情况:由于铁磁所有的自旋都指向一个方向 , 这种统一的构型不会引起空间反演对称性的变化(可以认为和空间是否反演没有关系) , 所以一般与铁电不耦合 。 同样 , 这一构型不会破坏空间反演对称 , 后面也会给出具体的分析图像 。 因此 , 可以看出 , 反铁磁材料的时间反演与空间反演密切关联 , 而铁磁材料的时间反演与空间反演关系不大 , 这也是为何很多的磁电耦合现象都出现在反铁磁材料中 。
好了 , 剩下的将 2 重、3 重、4 重旋转操作等加上时间反演的例子 , 笔者就不再具体说明 。 它们与上面详述的 6 重旋转加上时间反演操作的图像是类似的 。 这里重点说明一下 , 对一个中心对称的体系 , 原本对称性要求是不允许有极化产生的 , 但加上时间反演操作后 , 却可以产生极化 。 这是为什么呢?如何阐释这个极化的来源?
以六角晶格为例 , 如图 2(f) 展示了一个中心反演对称的反铁磁晶格 , 其自旋方向沿着 6 重旋转轴 。 首先考虑没有自旋的空间反演 , 可以得知其中一个空间操作是 – 6 。 因为是反铁磁 (箭头指向方向相反) , 再加上时间反演操作 , 就得到点群 – 6' 。 对应于 – 6 空间点群的点阵毫无疑问是非极性的 , 不允许有铁电极化 。
现在 , 加上一对反向的自旋时 , 就需要考虑两种情况:
(1) 不存在“外”磁场:这里“外”未必一定是外部施加的磁场 。 此时 , 整个空间晶格还是中心反演对称的:虽然反向自旋排列破坏了六重旋转轴 (操作元素由 – 6 变成了 – 6' ) , 但中心反演对称依然保持 。 这种操作依然会将自旋可能造成的铁电极化给转没了 , 对应的微观物理图像是原子外层电子云呈现对称分布 , 整体没有铁电极化产生 。 也就是说 , 无磁场时 , 这一体系没有铁电性 。
(2) 存在“外”磁场:此时 , 反铁磁态的哈密顿量会多一项磁场引起的塞曼能 , 两个原子或者说自旋的哈密顿量不再相等 , 类比这里的两个自旋不再等价 。 具体表现是:因为自旋反平行 , H 对一个自旋来说是 + H , 对另一个自旋来说是 – H , 导致原子核外电子云畸变不等 。 这种电子云的偏移 , 造成空间对称破缺 , 产生铁电极化 。
当然 , 说得再多 , 不如一个例子来得形象 。 可以想象 , 反铁磁使得满足 6' 这种时间反演对称破缺的两个粒子 (自旋) 在外磁场下不再一样 , 可能一个粒子“重”、另一个“轻” 。 然后 , 加上空间反演 – 6' (也就是空间中大小相等方向相反的力) , 这时“轻”的粒子就会被拉离平衡位置较远 , “重”的粒子被拉离平衡位置较近 , 空间反演对称也就被打破了 , 最终产生了铁电极化 。
值得强调的是 , 这种图像所基于的只是电子云密度分布上的差别 , 因此此类多铁性产生的铁电极化普遍很小 。 所有对称性的讨论也是基于一个基本假设:即电子云的畸变不会改变原本点阵的非极性对称性 。 当然 , 这也反过来预示了:好的磁电材料最好是空间和时间反演同时破缺 , 且相互耦合 , 如此之铁电性能才可能更好!
对此类多铁微观物理机制 , 即磁结构与铁电极化的关系起源 , 需要对三种自旋有序结构诱导铁电的微观模型有所了解 , 即交换收缩机制、自旋流机制、p – d 杂化机制 。 具体的物理这里就不再详细阐述 , 感兴趣的读者可以参阅一些相关的文献 。
写到这里 , 目前的几种常见对称操作已展示完毕 。 笔者希望通过对具体的点群 – 6' 展开描述 , 使没有接触过这一领域的读者明白对称操作和磁电耦合之间的“紧密”关系 。 当然 , 有关对称操作与磁电耦合关系的更严谨描述 , 读者可参阅 S. -W. Cheong最近撰写的《SOS: symmetry - operational similarity》一文 (npj Quantum Materials 4, 53 (2019) [2] 。 本文的描述 , 自我感觉比较形象直观 , 大概要比 Cheong 的文章更容易理解^_^ 。 读者如感兴趣 , 可以私下自己试着分析其它点群的情况 , 并不复杂 。
接下来 , 笔者意欲从这些简单的对称操作图像出发 , 通过几个具体工作 , 来展示对称操作在磁电耦合或者多铁性材料中的应用 。
4. 走马观花
近十几年来 , 随着第II 类多铁出现 , 磁电耦合研究形成了一波高潮 。 各种老的、新的磁电材料都被人们拿来“反复”研究 。 这些磁电材料形式多样、各有千秋 , 让人感觉很杂乱 。 这种状况 , 对做物理的人来说很头疼 , 因为物理人都喜欢简单的模型、统一的理论… 。 所谓大统一、终极理论 , 等等 , 您还想怎么样?!
幸运也不幸的是 , 纵然这些磁电材料有“七十二般变化” , 也始终没有逃出对称性的“手掌心” 。 下面 , 我们就跨上一匹小驴、走马 (骑驴) 观花 (看唱本) 。
4.1. 经典实例 (Cr2O3)
磁电耦合经典材料 Cr2O3 , 如“祖师爷”般存在 , 是这个领域的物理人写论文引言时必提的“大佬” 。 其空间点群为中心对称的 – 3m , 如图 3(a) 所示 。 这里的 – 3 就是平行于 c 方向的三重旋转轴 , 体系不允许有铁电极化 。 这一点在上一节已经讲过 , 这里就不费口舌 , 只将重点放在磁电效应与对称操作的关系上 。
对于 Cr2O3 , 当温度低于 Neel 点 TN ~ 307 K 时 , 形成反铁磁长程序 。 将空间点群加上时间反演破缺的操作后 , 磁点群就成了 – 3'm' (其中 – 3' 是满足三重旋转对称、且呈现反铁磁的点群 , m' 是垂直于 a 方向的镜面对称、呈现反铁磁之点群) 。 为简单起见 , 这里我们只介绍 c 方向三重旋转轴的情况 。
图 3(b) 展示了外加电磁场为零时的情况:可以看出 , 此时体系的电偶 (磁偶) 极子都相互抵消 , 整体依然处于中心对称状态 , 净磁矩和电极化为零 。
存在外电场时 , 如图3(c) 所示 。 外电场使得带正电荷的 Cr3+ 沿着电场运动 , 而带负电的O2- 沿着电场反方向运动 , 如图中标记的两个电偶极子 。 这样的运动 , 导致上面的偶极子极化减小、下面的偶极子极化增大 。 它们不能相互抵消 , 产生净极化 。 另一方面 , 从磁矩来看 , 按照DMi ~ αji Ej 的线性磁电关系 , 外加电场 , 同样会产生额外的磁电关系项 (± g μB α E ) , 使得反平行排列的一对自旋能量发生劈裂 , 与上面提到的加磁场是一样的 。 可以想象成沿着电场正方向的粒子变“重” , 反方向的粒子变“轻” 。 正因为这种电子云畸变 , 磁偶极子不能相互抵消 , 同样也就产生了净磁矩 。
存在外磁场时 , 如图 3(d) 。 实际的物理图像和外加电场类似 , 不过理解起来却不能与之“混为一谈” 。 不同于外加电场 , 外加磁场直接影响的是电子轨道 。 磁场势必引入塞曼能 , 造成电子轨道畸变 , 产生净磁矩 。 反过来 , 由于畸变的电子轨道间相互作用 , 势必会造成电子云不对称 , 使得电偶极子在电子层面上不能相互抵消 , 也就产生了电子极化 (Dpi ~ αij Hj ) 。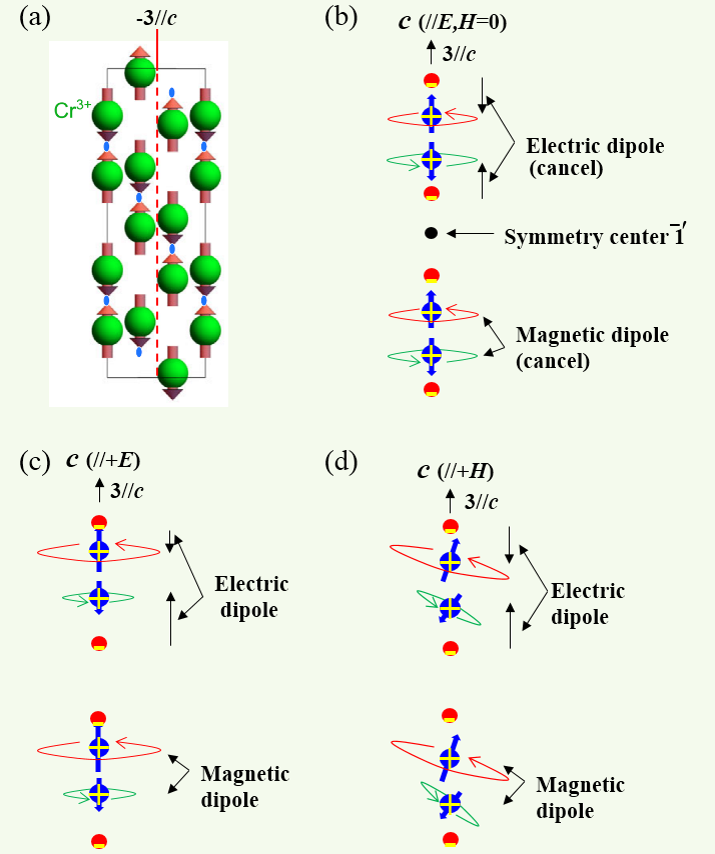
本文图片
图 3. (a) Cr2O3 的磁结构 [2] 。 (b) 外加电磁场为零时的磁点群示意图 , 此时电 (磁) 偶极子相互抵消 , 没有净磁矩和极化 。 (c) 外加电场引起正负电子反向移动 , 诱导净极化和电场诱发的净磁矩 。 (d) 外加磁场诱导的净磁矩和磁矩诱发的电极化 。
总结一下 , 依据图3 给出的物理图像 , 相信外行读者对磁电耦合的具体过程已经有些印象 。 而细心的读者可能也留意到 , 磁矩或者铁电极化的产生 , 都伴随着对称的破缺 。 这些破缺 , 或是因为外电磁场直接诱导的 , 或是因为电子之间的相互作用 (实际上主要是库伦相互作用) 引起的电子云畸变导致的 。 由此 , 可以概括一下此类磁电效应与对称性之间的某些关系 。
一个中心对称的体系 , 加上时间反演破缺操作后 , 就可以存在铁电极化 。 例如 , 对 Cr2O3 , 其磁点群的一个操作元素为 – 3' , 这一对称性操作等价于中心反演对称操作 (- 3) 加上时间反演破缺操作 (3' ) 。 这一复合操作的最终“表象” , 与不进行中心反演和时间反演破缺的对称性操作 3 是一样的 , 而对称性 3 却允许沿 c 轴方向的铁电极化 。
这样说颇为拗口 , 有些读者可能还不能理解 。 让我们先把思路调回到第 2 节讲的那个只有三重旋转轴 (也就是对称操作 3) 的模型 。 因为面内的对称限制 , 面内不能允许有极化产生 。 但是 , 沿着三重轴方向却没有对称性限制 , 这时外加正反电场是可以调控原子位移的 , 从而改变极化 。 同样 , 在这里 , 对满足 – 3' 操作的磁点群 , 也就是中心反演对称操作 ( – 3) 加上时间反演破缺操作 (3' ) , 并没有对三重转轴方向施加对称限制 。 因此 , 这些对称操作同样也允许转轴方向出现铁电极化 。 更进一步说 , 磁点群 – 3' , 与晶格点群 3 , 从对称性操作角度来看很类似 。 这一具体的图像也正好解释说明了上一节提到的时间反演加空间反演联合操作并不改变对称性的性质 (即 CP 反演对称) 。
其实 , 这里的物理机制是有实质性差别的 。 操作 3 对应的是原子位移 , 铁电极化往往很大 。 而操作 – 3' 对应的却是电子畸变 , 铁电极化往往较弱 。 所以 , 我们说它们只是从对称性角度拥有类似的“表象” 。 总结成一句话就是:一个对称操作 , 如果允许铁电极化存在 , 再经历后续的中心反演对称和时间反演破缺两次操作 , 其结果是回到最初的对称操作本身 , 还是允许铁电极化出现 。
有读者会说 , 你这样的推理到底对不对?有没有实验结果验证呢?答案是肯定的 , 如图 4(a) 和 4(b) 分别展示了 Cr2O3 实验观测到的磁电效应 , 即磁场诱导了铁电极化和电场诱导了净磁矩 。 其中 , 图 4(a) 的插图中更是直观展示了外磁场存在时铁电回线的测试结果 。
同样 , 对于其它旋转操作(1、2、4、6) 或者镜面操作 (m) , 也是同样的结果 。 当同时存在这两个操作元素时 , 就会有磁场诱导型的铁电极化 。 重庆大学柴一晟老师最近报道的Fe4Nb2O9 体系 (PRB 103, L140401) , 其中给出了 – 1' 的磁点群 。 这一点群分析 , 与他在实验上测到的不同方向极化数据完美地展现了一一对应的密切关系 。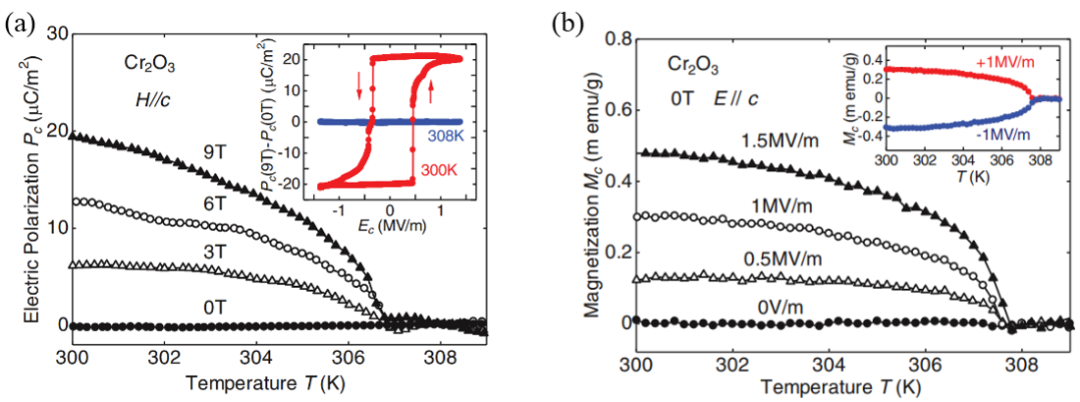
本文图片
图 4. (a) 外加沿 c 方向的不同磁场 , 诱发 c 方向的铁电极化 。 插图为外加 9 T 磁场时的铁电回线 。 (b) 外加 c 方向电场诱发的磁矩 , 插图为正反电场诱导的净磁矩 [3] 。
4.2. 荧光几点
读到这里 , 若是理解了以上磁电图像 , 那再遇到晶格点群或者磁点群时 , 我们就能对基本的磁电性质预测一二 。 如此一来 , 似乎又让读者感觉到磁电耦合也还是不过如此 。
其实还是不然 。 下面再展示几个有所不同的实验结果 。
最近受关注的极性磁体 M2Mo3O8 (M = Fe、Mn、Co、Ni ) 是一个很好的例子 。 这一家族 , 室温下就展示出极性空间结构 (晶格空间群为 P 63cm ) 。 为简单说明 , 就以 Co2Mo3O8 和 Ni2Mo3O8 这两个体系的 c 方向为例 (其它 M = Fe、Mn 等都与 Co 类似 , 不再赘述) 。
对 Co2Mo3O8 , 温度低于 TN 时 , 展现出明显二阶磁电效应 。 也就是说 , 当外加磁场沿着 c 方向时 , c 方向的极化随磁场呈现二次方的关系 。 借助中子散射知道 , Co2Mo3O8 的反铁磁转变温度为 40.5 K 。 考虑自旋后 , 反铁磁转变温度以下的磁点群变为 6'mm' 。
与 Co2Mo3O8 有很大区别的是 , Ni2Mo3O8 拥有复杂的非线性结构 , 面内呈现出条纹状 , c 方向呈现出锯齿状 , 反铁磁转变温度在 5.5 K 附近 。 它的磁点群是正交的 2'mm , 不同于其它 M2Mo3O8 (M = Fe、Mn、Co) 的六角磁点群 。
确定了磁点群之后 , 便能分析磁电耦合性质 。 这里就以 c 方向的对称操作为例进行描述 。
不同于上面介绍的 – 6' 和 – 2' , 这里的 6' 和 2' 缺少一个空间反演对称操作 。 图 5(a) 和 5(b) 分别展示的是满足 6' 和 2' 两个操作的物理图像 。 对这两个操作 , 同样很好理解 , 因为没有空间反演对称限制 , 粒子可以在这个方向无“束缚”运动 。 也就是说 , 可以有自发极化产生 。 图 5(c) 和 (d) 分别展示了 Co2Mo3O8 和 Ni2Mo3O8 在外磁场为零时的自发极化 [4] [5] 。
特别想强调的是 , 这里的自发极化是反铁磁序形成时产生的 。 想象一下 , 顺磁态时 , Co2Mo3O8 和 Ni2Mo3O8 晶格点群都是 6mm , 操作 6 是沿着 c 方向的六重旋转轴 , 其图像就是一个传统的热释电体 , 与第 2 节的描述无异 。 当反铁磁序形成 , 考虑极化时必须引入电子自旋有序排列的效应 , 虽然这个效应对离子型位移的影响较弱 。 通过中子散射 , 可以看到 Co2Mo3O8 在由顺磁进入反铁磁态时 , 钴离子沿 c 发生了位移 , 直接证明了自发极化的晶格起源 。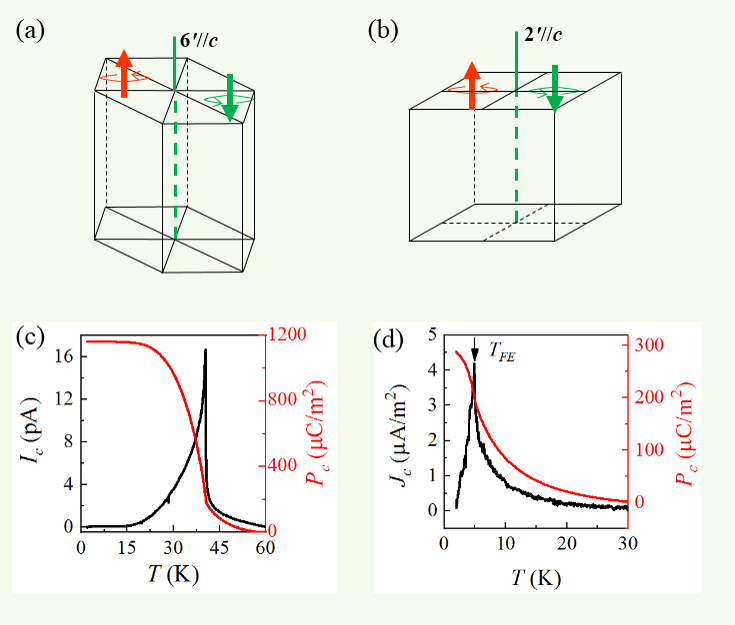
本文图片
图 5. (a) (b) 操作 6' 和 2' 的物理图像 。 (c) 在外场为零时 , Co2Mo3O8 单晶沿着c (// 6' ) 方向的热释电流和自发铁电极化 。 (d) 外磁场为零时 , Ni2Mo3O8 单晶在c (// 2' ) 方向的热释电流和自发铁电极化 。
看磁电耦合 , 当施加沿 c 方向的磁场时 , 同样地旋转轴方向没有空间对称性限制 。 对反铁磁态自旋 , c 方向的外磁场 Hj 引入塞曼能 , 使两个自旋的哈密顿能发生劈裂 。 这种情况下 , 可以想象成两个自旋一个变“重”、一个变“轻” 。 这样的一对自旋或者离子 , 因为没有空间对称性限制 , 外加一个外磁场 Hk 便可以诱导出铁电极化 。
需要强调两点:(1) 这里考虑的是磁电耦合 , 即 P – H 关系 , 是在恒温下测量的 , 所以由温度诱导的原子型位移可以忽略 , 只需要考虑磁场对电子的影响 。 (2) 这里提到两次加磁场 Hj Hk , 很有点意思 。 这里说的两次 , 并不是指先后次序关系 , 而是一个磁场的两种效果 。 因为是反铁磁排列 , 在不加磁场时 , 电子云排布对称 。 “第一次”加磁场 , 两个自旋看起来一个“重”、一个“轻” 。 这个比喻很好地图示化了两个自旋对外场或者外力的响应 。 在“第一次”磁场基础上“第二次”加磁场 , 相当于驱使两个“已经不同”的原子再发生不同的位移、再产生铁电极化 。 由此 , 可以大概说明连续“两次”加磁场 Hj Hk , 相当于得到极化与磁场的二阶关系 , 如图 6(a) 所示 [4] [5] 。 如此图像 , 看起来有些强词夺理 , 但很好使!
接下来再延伸一下 。 当施加的磁场更高 , 使得两个自旋平行排列时 , 结果如图 6(b) 所示 。 此时 , 对应的操作就由反铁磁的 6' 变成了铁磁态的 6 。 这一物理图像也好理解:不同于反铁磁 , 这时就算加磁场 , 两个原子的哈密顿能总是相等的 , 外加磁场同时改变两个离子的电子云 , 产生的位移方向是同步的 , 即线性磁电效应 。 这一图像很好说明了为什么图 6(b) 所示的高场部分是线性变化 。 同样 , 如此图像 , 看起来有些强词夺理 , 但很好使!
值得提出的是 , 这里的第二种情况 , 即二阶磁电耦合 , 是笔者自己根据感觉“瞎扯”出来的 , 有没有合理的一点成分还有待方家评点 , 虽然笔者自己感觉还算合理 。 有关其它结果的物理讨论 , 文献中都有相关报道了 。
总结一下 , 通过对 Co2Mo3O8 和 Ni2Mo3O8 这两个具体材料的磁点群分析 , 我们得到了与实验相同的结果:对不满足空间反演对称操作、而只满足时间反演破缺操作的对称性 , 例如 1'、2'、3'、4'、6' , 允许有二阶磁电效应 。 而对考虑自旋后的 1、2、3、4、6 等操作 , 允许有线性磁电耦合效应 。 这一具体图像同样很好地解释了第 3 节中 , 我们提到的为何在铁磁材料中时间反演破缺 , 与空间反演破缺与否没有关系;而反铁磁引起的时间反演破缺却与空间反演破缺密切关联 。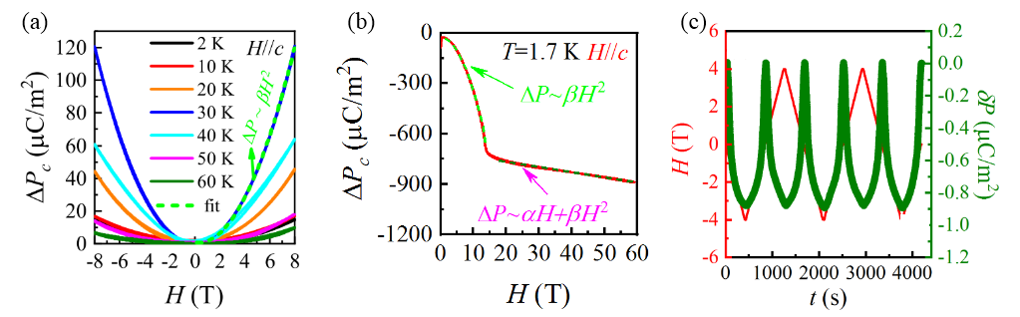
本文图片
图 6. (a) 不同温度下 , Co2Mo3O8 单晶 c 方向的铁电极化与磁场呈二次方关系 (DPc ~ β H 2) 。 (b) 在T = 1.7 K , Ni2Mo3O8 单晶 c 方向的铁电极化与外加高磁场的关系 。 其中 , 低磁场区域的极化与磁场呈二次方关系 (DPc ~ β H 2) , 高磁场主要呈线性关系(DPc ~ aH + β H 2) 。 (c) Yb0.42Sc0.58FeO3 多晶在 T = 2 K 时铁电极化与磁场的关系 。
这里 , 请容忍笔者再放肆一回 , 评点一二 , 对线性和非线性磁电耦合作一些讨论!
我们知道 , 描述空间点群时 , 有 10 种能允许出现极化的点群 (包括 1、2、m、3、... 等) 。 我们说这些点群是极性点群 , 它们描述的是离子型位移 。
提及磁电耦合的磁点群时 , 目前允许有线性和非线性磁电耦合的磁点群一共有 122 种 。 首先 , 这些磁点群 , 在空间点群那里可以是极性的、也可以是非极性的 。
对非极性的空间点群 , 它们的磁点群是不是极性的呢?我们只能说 , 描述磁点群时用的“极性”表面上与描述空间点群的极性是一样的 , 但是它们本质不同 。 磁点群描述的是电子云的畸变造成的对称与否 , 这一点与空间点群不同 。 所以 , 一般情况下我们很少用“极性”这个词来描述电子云畸变的图像 , 虽然本质上都是不对称 。
读者应该也发现了 , 最终铁电极化的产生 , 要不就是离子位置不对称 , 要不就是电子云不对称 。 反正都是不对称 , 所以如果“极性”描绘的是不对称 , 那似乎就可以用来表示这些极性的关系 。 但是 , 目前这种表述好像还没普遍使用和认可 , 读者也许应该自行去领会其中的区别和联系 。
4.3. 夜未央
对多铁性而言 , 笔者狂妄 , 以为尚在长夜漫漫、晨曦初露、还没有到拂晓和旭日 。
第一 , 对称性描述的只是磁电耦合等物理效应是否有可能 。 对称性图像对具体物理机制的预言或揭示并不能有多大作为 。 在应用对称性分析的时候 , 还是应该基于物理图像的理解 , 不然就会显得有点“空嘴说白话” 。
第二 , 对称性分析 , 在描述多晶样品时 , 显得苍白无力 。 一个例子是多晶稀土六角铁酸盐 (Yb0.42Sc0.58FeO3) 。 通过中子散射 , 我们得到体系由顺电相进入铁电相后 , 磁点群变为 6m'm' [6] 。 由于 c 方向 Fe3+ 自旋倾斜 , 引入了弱铁磁性 , 使得 6 重旋转对称保持不变 (如果是 c 轴反铁磁排列 , 那就变成 3 重轴旋转对称了) 。 当温度降到 40 K 以下 , 随着 Yb3+ 磁性引入 , 对应的磁点群变为对称操作更少的 6 。 最后 , 不管是 6m'm' 还是 6 , 都允许出现磁电耦合 。 然而 , 我们的实验只在低温部分测到了很弱的磁电效应 , 如图 6(c) , 完全看不出是线性磁电行为 , 而且也没有办法标定磁电耦合的各向异性 。 即便可以给出很具体的对称分析 , 但读者大可以不相信 , 因为没有实验数据证明 。
笔者所遭遇的就是如此:审稿人直接让我们给出不同方向的耦合系数 。 我们只能无语 , 因为多晶样品没法给出这些数据 。 最后 , 我们也只能删除那些对称性分析 , 虽然它们耗费了我们老鼻子心血 。 所以 , 要想更好地说明对称性问题 , 还是必须长单晶 。
第三 , 本文所陈述的很多图像或描述并非从教科书中摄取 , 乃笔者自己瞎琢磨的心得 , 很多看起来并不是很准确 。 这和笔者的知识体系还不是很完备有关 , 谨致歉意 。
5. 总结与展望
行文至此 , 主要内容已经讲得差不多了 。 当然 , 很多深入的讨论这里并没有涉及到 , 因为从科普文角度来撰写 , 笔者感觉有些江郎才尽 。 好吧!我承认本文不大科普 , 甚至有点乏味 , 这里就辛苦读者忍着看了 。
其实 , 简单来说 , 主要是想用这三个具体实例 , 给读者展现一下如何通过对称性分析来预测材料中铁电极化的有无及方向 。 关键在于 , 对一些中心对称的晶体 , 当知道磁空间群后 , 这种分析能给出:磁电效应存不存在?沿着哪个方向允许有极化?怎么加磁场能诱导出极化?等等 。 正如图7所示 , 对我们做实验的人来说 , 这是有价值的知识体系 。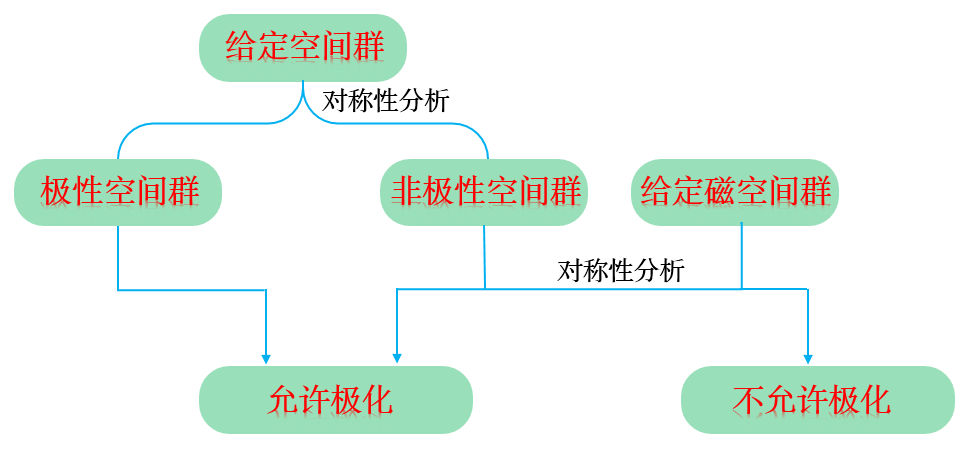
本文图片
图 7. 在给定空间结构和磁结构后 , 分析磁电材料的磁电效应性质的流程图 。
毫无疑问 , 如果做实验只是讲对称性 , 那是乏味的 。 果若如此 , 物理人只需要测量出样品的空间群和磁点群 , 就一览其铁电性和磁电耦合了 。 的确 , 目前的磁电耦合材料有点这个味道 , 似乎磁电耦合的研究似乎到了瓶颈区 。 但是 , 正如 Ising 老师说的 , 做物理的人不应该是这样的 , 应该去深入探究其中物理机制、寻找有应用价值的磁电材料 (因为虽然发现的磁电材料很多 , 但是离应用还有差距);或者 , 应该向其它领域开拓 。
例如 , 最近物理人关注的磁电材料 Cu2OSeO3 , 就揭示出外加小磁场能激发出磁斯格明子 , 展现出自旋型的拓扑序 [7] 。 还有一些磁电材料 , 能展现拓扑磁振子性质 。 另外 , 磁电材料与目前受关注的铁环 (ferrotoroidic) 也有直接关系 , 例如铁环要求材料必须是磁电耦合材料 , 并且非对角的磁电耦合系数相反、非零 , 等等 。
磁电材料 , 看似已经历经沧桑的领域 , 却总是充满 “意外” 。
最后 , 非常感谢读研这几年 Ising 老师和林林老师 , 他们对我多有指导和帮助 。 也感谢 PLD 所有的师兄、师弟、师妹们 。
参考文献
[1] T. Kimura, T. Goto, H. Shintani, K. Ishizaka, T. Arima and Y. tokura, Magnetic control of ferroelectric polarization, Nature 426, 55 (2003).
[2] S. -W. Cheong, SOS: symmetry-operational similarity, npj Quant. Mater. 4, 53 (2019).
[3] A. Iyama and T. Kimura, Magnetoelectric hysteresis loops in Cr2O3 at room temperature, Phys. Rev. B 87, 180408(R) (2013).
[4] Y. S. Tang, S. M. Wang, L. Lin, Cheng Li, S. H. Zheng, C. F. Li, J. H. Zhang, Z. B. Yan, X. P. Jiang, and J. -M. Liu, Collinear magnetic structure and multiferroicity in the polar magnet Co2Mo3O8, Phys. Rev. B 100, 134112 (2019).
[5] Y. S. Tang, J. H. Zhang, L. Lin, R. Chen, J. F. Wang, S. H. Zheng, C. Li, Y. Y. Zhang, G. Z. Zhou, L, Huang, Z. B. Yan, X. M. Lu, D. Wu, X. K. Huang, X. P. Jiang, and J. -M. Liu, Metamagnetic transitions and magnetoelectricity in the spin-1 honeycomb antiferromagnet Ni2Mo3O8, Phys. Rev. B 103, 014112 (2021).
[6] Y. S. Tang, S. M. Wang, L. Lin, V. Ovidiu Garlea, T. Zou, S. H. Zheng, H.-M. Zhang, J. T. Zhou, Z. L. Luo, Z. B. Yan, S. Dong, T. Charlton, and J. -M. Liu, Magnetic structure and multiferroicity of Sc-substituted hexagonal YbFeO3, Phys. Rev. B 103, 174102 (2021).
[7] S. Seki, X. Z. Yu, S. Ishiwata, Y. Tokura, Observation of skyrmions in a multiferroic material, Science 336, 198 (2012).
备注:
(1) 笔者乃南京大学物理学院博士生 , 主要研究兴趣为磁电耦合材料 。
(2) 文首处的小诗为 Ising 所撰 , 表达磁电材料人对“对称性”的敬畏和牢骚 。
(3) 插图 1(b) 来自网络 。
(4)感谢东南大学董帅教授的指点 。
来源:量子材料QuantumMaterials
【原子|磁电耦合的对称之约】编辑:aloysius
推荐阅读
- IT|通用原子公司的新型Mojave无人机拥有16枚地狱火导弹的强大威力
- 国际化|全球首个回旋加速器国际标准发布,中国原子能科学研究院主导编制
- 分系统|小米 MIUI 开发版第 524 周公告:部分系统 App 解耦合,可升级
- 纪念版|红米 Redmi Note 11 Pro 推送MIUI 12.5.8更新:新增原子内存功能
- 原子|怎么解释摩擦力的本质是电磁力?
- Huawei|华为正式捐赠欧拉给开放原子开源基金会
- 科技|什么是耦合?
- 速度|高精度原子钟
- 原子|世界上分辨率最高的照片,甚至可以看清原子的模样!
- the|通用原子、波音将为美陆军打造300kW目标追踪激光武器