【行测数量关系:假币在哪里,一眼就发现】
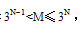
在行测数量关系中 , 真假币问题属于统筹问题中的一种 , 需要结合题意统筹规划 , 全面分析 , 做起来耗时费力 。 但是如果能掌握做题技巧 , 真假币问题反倒是可以秒解的题型 。
真假币问题 , 即描述在若干枚外观相同的硬币中 , 混有一枚质量不同的假币 , 其余均为真币 , 若用天平去称 , 求一定找出假币所需最少次数的问题 。 解决这类题目的原则是使每一次称量 , 筛选的硬币数量尽可能多 。
通过以下题目来感受一下真假币问题 。
例1国王准备难为一下阿凡提 , 给了他9枚金币 , 其中有一枚是假的 , 外形一模一样 , 但是重量偏轻 , 如果阿凡提找不出来 , 就要被关起来 , 阿凡提向国王要了一个天平 , 但是国王不给砝码 , 如果你是阿凡提 , 现在要帮助他找出哪个是假币 , 至少要使用天平几次?
A.1 B.2 C.3 D.4
【答案】B 。 中公解析:第一次 , 将9枚金币分成3组 , 每组3枚 , 任意取出两组进行称重 。 若两组一样重 , 则假币一定在第三组;若两组不一样重 , 则假币在轻的一组 。 所以无论是哪一种情况 , 均可以确定假币所在哪一组 。 第二次 , 将假币组的三枚硬币随机取出两枚进行称重 , 若两个金币不一样重 , 则假币在轻的一侧;若两个金币一样重 , 则假币就是第三个没有被称重的金币 。 因此两次即可找到假币 。
例28个外表一模一样的杯子 , 其中一个略重于其余7个 , 请问一台天平 , 最少称几次 , 一定可以找到这个略重的杯子?
A.5 B.3 C.2 D.4
【答案】C 。 中公解析:第一次 , 将这8个杯子尽可能均分 , 即分成三组 , 分别为3个、3个和2个 , 然后在天平两端各放3个杯子 , 如果平衡 , 即略重的杯子在2个组;如果不平衡 , 即天平重的那一端的3个杯子中含有略重的杯子 。 即可以确定略重的杯子在哪一组 。 第二次 , 如略重的杯子在2个组 , 此时将两个杯子放在天平两端 , 即可以确定略重的杯子是哪一个;如略重的杯子在3个组 , 此时随机选择两个杯子放在天平两端 , 如天平平衡 , 则第三个杯子为略重的杯子 , 如天平不平衡 , 则略重的杯子在天平重的一侧 。 所以最少需要两次即可找到略重的杯子 。
通过以上两道题目 , 我们可以总结如下结论:若有M枚硬币 , 其中一枚是轻一些(或重一些)的假币 , 则可利用限定条件即N的最小值为所求 。通过以上题目 , 我们发现真假币问题如果第一次接触 , 很难分析全面 , 但是当了解题型特征以及解题思路之后 , 就可以迎刃而解了 。
推荐阅读
- 男子深夜喝醉跑到山上睡着,醒来发现身边躺着一个妙龄女子
- 实拍非洲菜市场,跟中国差别很大,在市场上出现了一些中国制造
- 申彗星被逮捕!拒酒测车偷的,经纪公司回应酒驾属实,钥匙给错了
- 我们从北门进北海,南门出,正如古人说北海不过是一个城墙,一幢房子;但不幸的是,北海的城墙、房子都被挖光了






