
文章图片

文章图片
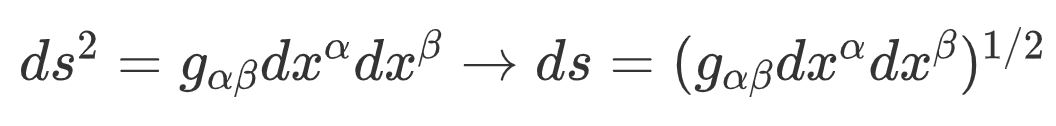
文章图片
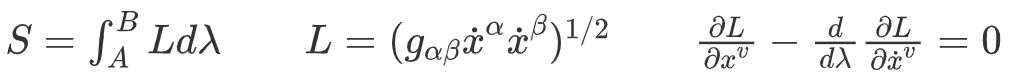
文章图片
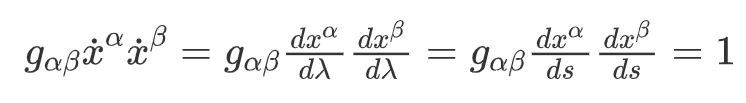
文章图片
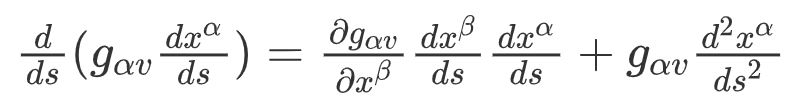
文章图片

文章图片

光是如何选择路径的?在公元40年左右 , 古希腊数学家海伦就提出 , 光会选择最短距离的路线 , 这被称为最小距离原理 。 但是 , 该原理无法解释光的折射 。 后来 , 在大约一千年以后 , 法国数学家费马提出 , 光沿着时间最短的路径前进 , 并以此原理解决了光的折射问题 。 事实上 , 凭借着最短
在这之后 , 科学家都在寻找更好的能最小化
上式L被称为拉格朗日量 , 而S被称为作用量 。 拉格朗日提出 , 自然界的运行总是以作用量最小为原则 , 后来这被称为最小作用原理 。 此外 , 他还从最小作用原理得出了拉格朗日方程:
有了这个式子 , 当我们从牛顿力学转向拉格朗日力学时 , 在对多体系统的计算中 , 会发现计算量明显少了很多 。 最小作用原理不仅可以在经典物理中使用 , 在量子力学和相对论中也可以使用 。 在前面的文章中 , 我们已经推导了拉格朗日方程 , 也介绍了它在费曼路径积分中的应用 , 今天我们就用它在广义相对论下推导短程线/测地线 。
首先 , 黎曼空间中A和B两点之间可以有无数条线 , 其中取极值的线称为短程线 , 线的长度为S:
其中 , 相邻两点之间的距离为ds , 它也称为线元:
引入标量型参量λ:
因此 , 线的长度S、拉格朗日量和拉格朗日方程的公式变为:
把拉格朗日量代入拉格朗日方程得到:
当我们把λ选择为线长S时 ,
所以 , (1)式可化简为:
其中 , 减号右边的项α=β合并了 , 又因为:
所以代入(2)式可继续变形为:
注意到:
于是(3)式可继续写成:
利用克里斯多菲符号与度规之间的关系 , 我们最终得到:
【利用最小作用原理推导广义相对论的运动方程】这就是黎曼空间中的短程线/测地线方程 , 也就是广义相对论的运动方程 , “物质告诉时空如何弯曲 , 时空告诉物质如何运动”的下半句 。 顺便说一下 ,
推荐阅读
- 美国载人登月有多么假?
- 首次发现!黑洞背后有回声光线,究竟什么样?
- 新药研发进入新时代:首次提出“以患者为中心”的药物研发理念
- 海水为什么又苦又咸不能喝?网友:长见识了!
- 他们分别发现和诠释了万有引力,堪称人类历史最伟大的两位科学家
- 爱因斯坦一生中犯的最大的错误!宇宙大爆炸破坏了时间平移不变性?
- “不完美”一点也不遗憾,它甚至是宇宙的基本规律!
- 地球速度:一天3200万公里在宇宙中飞奔!移动速度到底有多快?
- 没有天敌的生物——邓氏鱼,竟能将5000千克的岩石咬成粉末?




