
文章图片
文章图片
文章图片
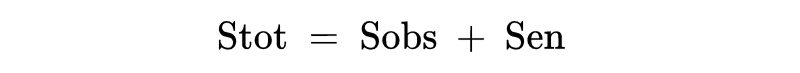
文章图片

文章图片
量子信息守恒(用冯·诺依曼熵来量化)是量子力学线性和幺正性的一个基本结果 。 由于信息和熵这两个术语在许多科学分支中被( 可交换地)使用 , 这对熟悉热力学第二定律的人来说可能听起来很奇怪(热力学第二定律说熵通常随时间的推移而增加) , 信息和熵怎么可能是一致的呢?
对于哈密顿系统 , 动力学总是可逆的 , 所以信息是守恒的(根据刘维尔定理) 。 人们可能会想 , 如果熵是一种信息的度量 , 那么对于一个经典系统 , 熵是如何增加的?
哈密顿系统是一个受哈密顿方程支配的动力系统 。 在物理学中 , 这个动力系统描述了物理系统的演化 , 如行星系统或电磁场中的电子 。 这些系统可以用哈密顿力学和动力系统 理论来研究 。
简短的回答
刘维尔定理是经典统计力学和哈密顿力学中的一个关键定理 。 它断言相空间分布函数沿系统轨迹是恒定的 。
刘维尔定理所描述的熵(或信息)与第二定律所讨论的熵并不相同 。 后者是指隐藏信息的数量(宏观测量无法获取的信息) , 而前者是一个系统的总信息量 。 换句话说 , 热力学的不可逆性是一种统计效应 , 与经典力学/量子力学的可逆性并不冲突 。
什么是熵和信息?
尽管如此 , 这个问题比它看起来更复杂 , 所以让我们深入研究一下 。
“熵”一词在不同的环境中使用 , 有不同的概念 。 我们在信息论(香农熵)、统计热力学(玻尔兹曼熵)和量子力学(冯·诺伊曼理论)中发现了熵 。 虽然它们都用相同的公式定义 , 但它们描述了不同的概念 。
玻尔兹曼将熵定义为一个符合系统宏观条件(宏观状态)的可能微观状态的数量的度量 。 冯·诺伊曼后来将熵的概念从经典统计力学扩展到量子信息论 , 克劳德·香农发展了类似于电信信号中信息随机损失问题的统计概念 。
在物理和信息科学中 , 信息和熵通常可以互换使用 。 事实上 , 熵可以被认为是一个信息的量度 , 它是用来陈述一个系统的微观状态所缺少的(隐藏)的信息 。
细粒度和粗粒度熵
换句话说 , 热力学熵反映了观察者在宏观测量条件下对系统微观状态构型的无知 。
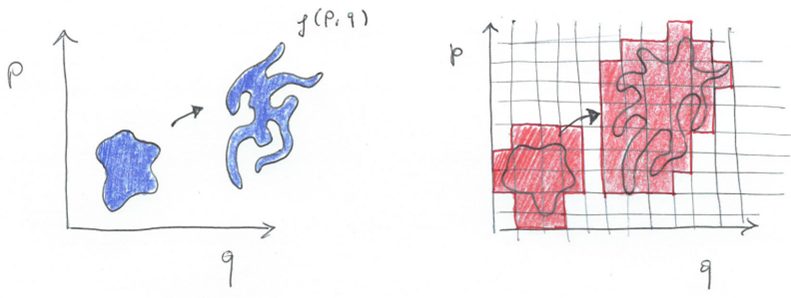
对系统的细粒度描述是对其微观行为的详细描述 。 粗粒度描述是对其一些细节进行平滑处理的描述 。 这种平滑让观察者忽略了
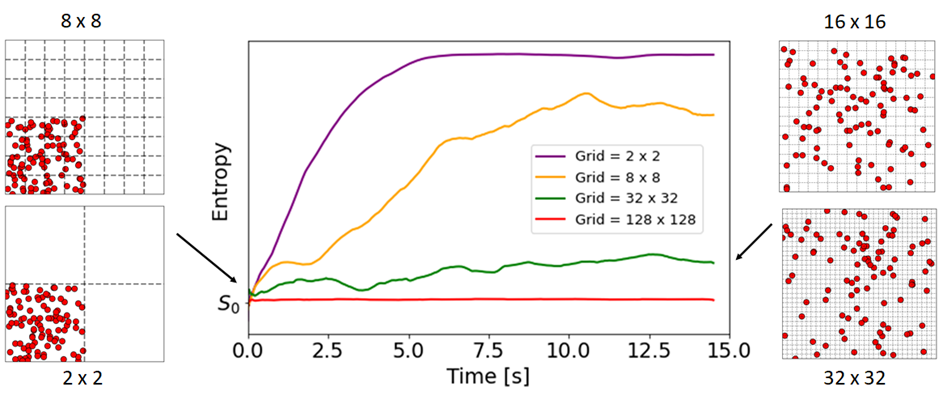
由于量子系统通常由它们的所有粒子描述 , 冯-诺伊曼熵通常是细粒度的 , 因此在量子刘维尔定理下是常数 。 另一方面 , 从观察者的角度来看 , 系统的粗粒度信息的数量可能会随时间的变化而变化 。 粗粒度熵因此可以被视为“观测熵”或“热力学熵” , 因为它测量了观察者所测量的宏观状态下隐藏的信息 。
- 粗粒度熵的抽象表示 。 (左)变换后的相空间体积保持不变 , 但从观察者的角度来看 , 体积会增加 , 因为观察者只能看到相空间的网格表示(右)
推荐阅读
- 一根针以光速和超光速撞击地球,会带来什么后果?答案让人害怕
- 黑洞和暗能量:哈勃如何发现宇宙最黑暗的秘密
- 霍金的4个可怕预言:1个成真,2个正在上演,人类要警惕了?
- 科学家根据宇宙怪异现象,给出宇宙未来的三种结局
- 量子纠缠可以推测平行宇宙,是否可以说明人无真正意义的死亡呢?
- 时间真的是物质?物理学家已证实:它可以被弯曲!
- 量子力学能从现在改变过去?诺奖得主:量子延迟实验已证实这一点
- 银河系以每秒600公里向一个引力源行进,引力为何这么大?
- 用四大证据解释,足以证明我们的世界是一个虚拟现实世界吗?




