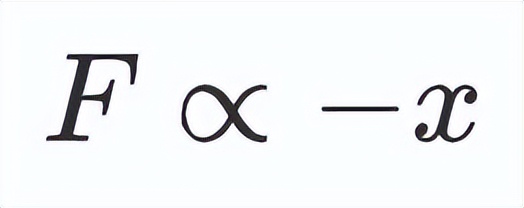
从胡克定律到量子力学的零点能量，最后还蹦出了拉马努金量子力学

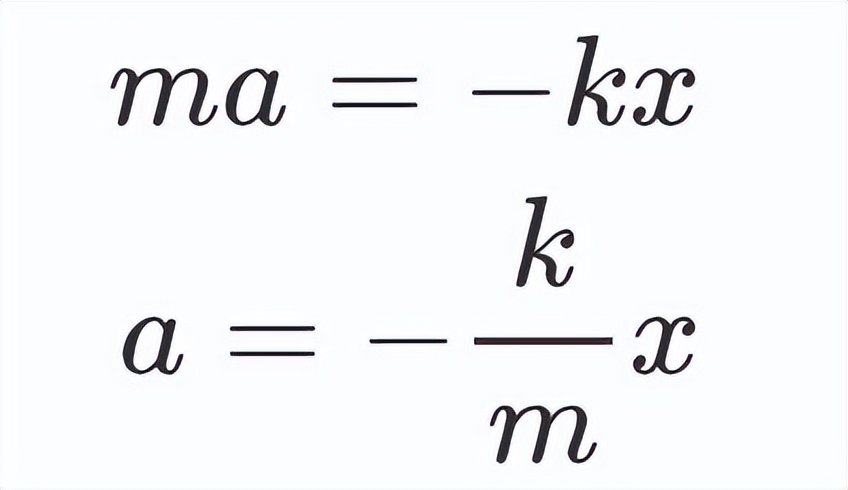
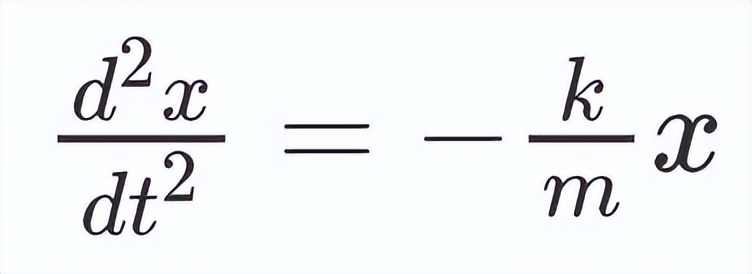
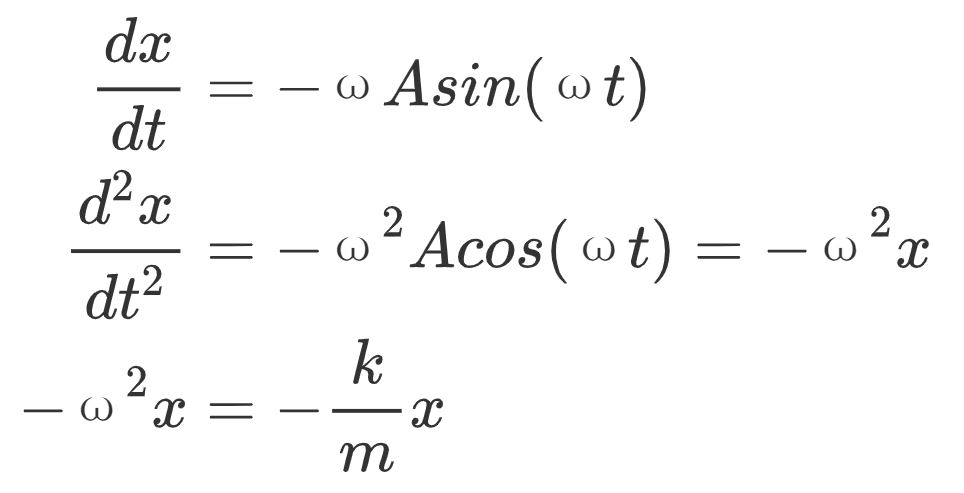
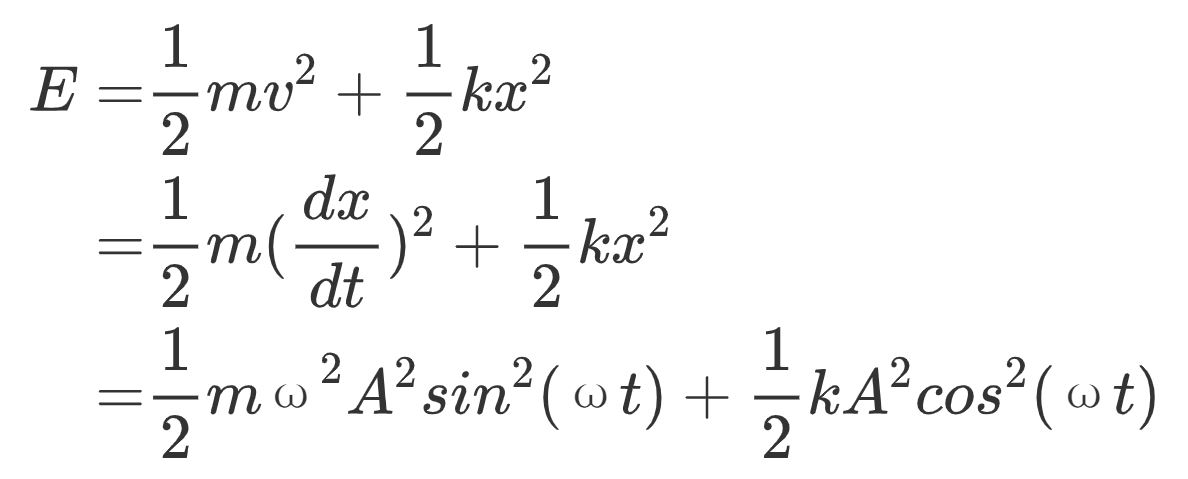
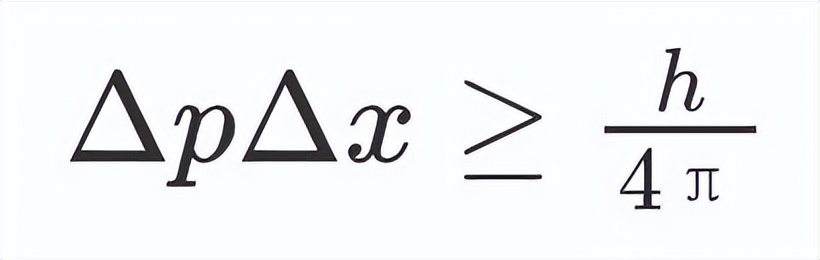
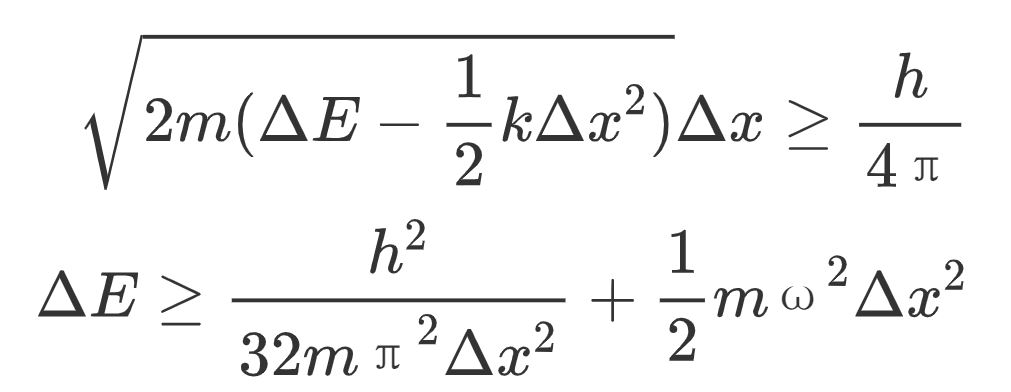
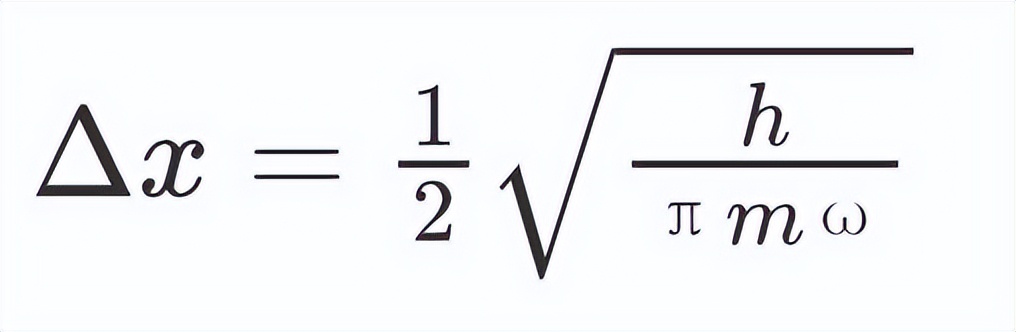
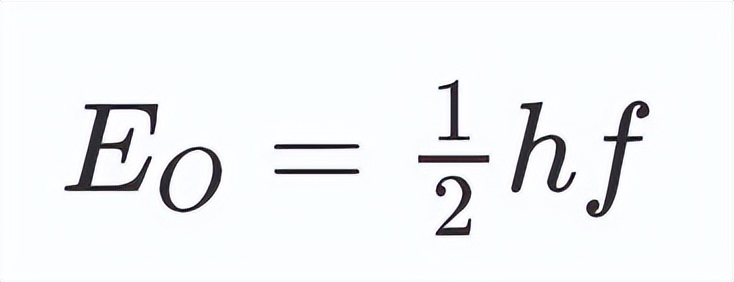
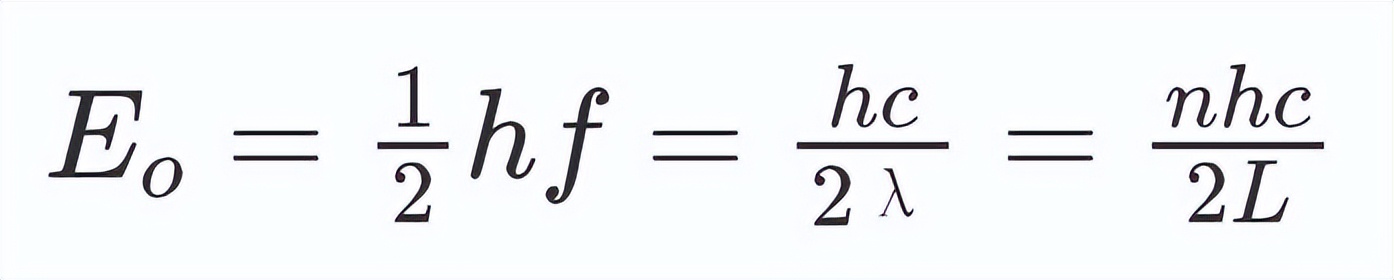
文章图片

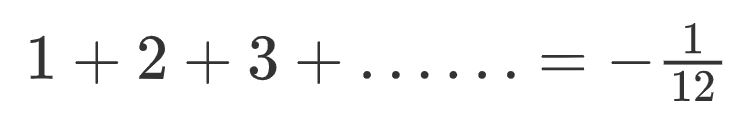
一个未拉伸的弹簧，一端固定在墙壁上，另一端系着一个质量为m的块状物体。如果我们拉动这个弹簧块并将弹簧延长一定距离x ，弹簧会对质量块施加恢复力F ，试图使质量块恢复到平衡位置。我们会发现，恢复力F与伸长量x成正比我们可以将其写成：

其中负号代表伸长量与恢复力的方向相反。
我们可以通过引入比例常数k来将关系转换为等式，这个常数k也被称为弹簧系数，是衡量弹簧刚度的一种量度。

考虑一下，如果把弹簧拉长后释放会出现怎样的情况？根据牛顿第二定律，弹簧力会导致质量加速，因此我们可以用ma代替弹簧力F ，并重新排列成如下公式：

上面这个公式实际上描述了一种特殊的运动类型：简谐运动，它是宇宙中各种振动的核心，为了更深入了解这个公式，我们将其写为二阶微分形式。

因此，结合加速度的二阶形式与胡克定律，我们就有了以下公式：

这个微分方程描述了弹簧的位移随时间的变化，我们知道它的解为：

然后，我们再将其两次微分后代入微分方程中：

因此，我们可以得到该系统的圆频率或周期：

我们还关心系统的总能量，它等于动能和势能之和，可以列出下式：

注意到ω与k的关系k=mω^2 ，我们可以得到总能量的公式：

到目前为止，这些都是些典型的推导，相信大家都已经滚瓜烂熟了。接下来，我们将把量子力学加上去。
零点能量真空中的最低能量称为零点能量，量子力学认为它非零，它是不确定性原理所要求的最小值。不确定性原理认为，我们不能同时精确地测量粒子的动量和位置，它的公式如下：

以弹簧系统为例，如果弹簧未伸展且处于静止状态，那么我们就精确地知道它的位置和它的动量，显然与不确定性原理相悖，所以量子弹簧存在最低能量的振荡。为了计算弹簧系统的最低能量，我们需要对能量公式进行些微修改：

我们将上式中能量E替换成ΔE ，动量p替换成Δp ， x替换成Δx ，代入不确定性原理的公式中：

由于能量不随x的变化而变化，所以我们有：

我们可以得到：

把它重新代入方程并简化，得到：

因此，我们可以得到量子振荡器的最低能量为：

卡西米尔效应
简单来说，在真空中的两片不带电金属板之间会产生吸力，这就是卡西米尔效应。量子场论认为，空间中都是振动的场，这些振动的场在金属板之间要满足边界条件，只有驻波才能存活下来。也就是说，只有整数倍波长等于板间距L的才能存活(nλ=L) ，其中n为整数，写成公式如下：

把所有这些波长的能量都相加起来，就有：

从胡克定律到量子力学的零点能量，最后还蹦出了拉马努金

推荐阅读

生饺子如何冷冻保存

雪莲果禁忌不得不知道

九层塔怎么保存九层塔的保存方法

滴滴出行在美上市远不是犯错那么简单

十一月的祝福语大全

抽象是什么意思通俗一点说

按摩用什么油好按摩用什么油好一点

酒糟发糕的做法（增肥食谱）

12月正能量的句子十二月励志的朋友圈句子

小松的社会趣闻红极一时的“包山头”养殖，如今却销声匿迹了，这是为何？

南方夏天温度高适合用有机水溶肥吗有机水溶肥的作用是什么

ios7怎么格式化

空调需要罩空调罩吗怎么才能挑选到好的空调罩

纳米手机膜是真的吗有多少人用过

老人吃早餐注意三宜三不宜

教你4点写好招商策划书写字楼招商计划方案怎么写

胸口起痘是什么原因呢？

鲟鱼的花式做法无敌小鲟鱼的做法

怎样自己练习瑜伽

蛋包肠怎么做