
文章图片
文章图片

文章图片

文章图片
我们处所的银河系估测恒星的数量就有1000-4000亿个 , 而在可观测宇宙范围内 , 像银河系这样的星系起码有数万亿个之多 , 那么理论上在半径为465亿光年可观测宇宙内 , 恒星的数量可以达到10^23这样的级别 。 有的朋友不禁产生了疑惑 , 像太阳这样一个恒星 , 就可以将地球面向它的一侧完全照亮 , 那么为何宇宙中这么多恒星 , 当夜晚的时候 , 没有将地球照亮或者天空为何是黑的呢?相信大家的第一直觉反应就是 , 其他的恒星距离地球太远 , 光线在传输过程中衰减得非常厉害 。 其实原因并非如此简单 , 如果按照宇宙中的物质是各向同性均匀分布、处于静态的观点 , 整个宇宙应该是完全明亮的 , 相信这个结果大家都非常震惊吧 。
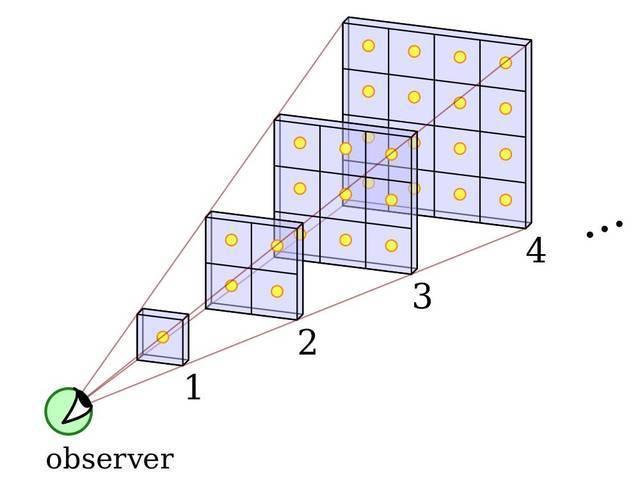
其实 , 早在19世纪20年代 , 就有科学家提出了这个问题 , 这位科学家就是德国科学家-奥伯斯 , 他假设我们处所的宇宙空间 , 是完全静止、均匀和无限的 , 如果令恒星的平均光度为Ln , 恒星在宇宙中的空间数密度为n , 那么在地球上 , 我们接收到的恒星发出光线的总照度可以用如下公式计算:
那么 , 当宇宙空间尺度无限大 , 即式中的r为无穷大时 , 我们可以发现地球所接收到的恒星总照度也趋向于无穷 , 显然这是不可能的 , 这个推导的过程就是科学界常说的奥伯斯佯谬 。 它所表达的观点 , 简单说就是在一个静止、均匀、无限的宇宙模型下 , 会出现黑夜与白天一样亮的推导结论 , 这与我们实际上观察到夜空却是黑的相矛盾 。
在奥伯斯提出这个观点之前 , 其实牛顿也根据当时科学界普遍认为的宇宙基本特性:均匀、静止的 , 以此为前提 , 假设宇宙的整体密度为ρ(不随着时间和空间的变化而变化) , 将可观测宇宙视为一个半径为R、质量为M的球体 , 那么相对于球心处 , 球体边缘的引力势能为:
那么 , 当R趋向于无穷大时 , 则边缘处的引力势能也趋向于无穷 , 这与牛顿万有引力大小与星体之间距离的平方成反比的结论相矛盾 。 在这种情况下 , 牛顿提出宇宙空间虽然是无穷大 , 但星体所受到的引力处于处处是平衡的结论 , 以此来消除这个与事实不符的佯谬 。
但是 , 通过上面两位科学家提出相应佯谬的推导过程 , 我们不难看出 , 它们都将引力和光的传播速度视为无穷大 , 即瞬时传播 。 然而 , 无论是引力还是电磁波 , 其都有传播的速度上限-光速 , 如果考虑无限远星体的引力、无限远恒星发出的光线 , 那么在地球上所接收到所需要的时间也将是无限长 , 所以如果对于无限的空间来说 , 这两个推导过程是不严密的 。
【宇宙中有那么多恒星,为何太阳落山之后,天空就变黑了?】与此同时 , 我们还需要考虑宇宙空间的膨胀效应 。 美国著名天文学家哈勃在长期观测的基础上 , 发现了来自遥远星系发出光线的光谱 , 有向红端移动的趋势 , 而且距离越远 , 红移现象越明显 , 因此提出了哈勃定律 , 即星系相对于地球的退行速度 , 与星系和地球的距离成正比 , 这个比值即为哈勃常数 。 2013年 , 科学家通过普朗克卫星 , 测算出哈勃常数值为每百万秒差距(326万光年)的区域 , 星系相对于地球的退行速度约为68公里每秒 。
宇宙膨胀的结果目前已经被科学家们通过大量的实验和观测所证实 , 这种膨胀并非是物质的膨胀 , 而是空间的膨胀 。 在空间膨胀的影响下 , 来自遥远星系发出的光线 , 则会在空间的不断拉大下 , 从目标源达到地球所经历的路程也相应地延长 。 这也就造成了在宇宙大爆炸时 , 即空间膨胀的起点期-138亿年前 , 所发生的第一缕光线 , 经历了465亿年才到达地球 , 这个465亿光年就是我们所能观测到的可观测宇宙 , 在这个范围之外 , 由于空间退行速度大于光速 , 我们永远也接收不到它们发出的任何信息 。
因此 , 造成奥伯斯佯谬的主要原因 , 则来源于宇宙空间的膨胀 , 以及由此带来的电磁波传播速度的延长 。 而在空间膨胀效应的直接影响下 , 我们能够观测到的宇宙空间范围又是有限的 , 从而恒星的数量也是有限的 , 对于宇宙空间中的低物质密度来说(每立方米仅有数个质子的水平) , 按照黑体吸收能量的规律 , 星际物质也不可能吸收无穷多的能量 , 再加上电磁波在近乎真空中的传播势必会受到一定程度的阻挡 , 过程中会发生能量的吸收、反射等现象 , 相当于所有恒星体发出的光线 , 是通过了一个具有衰减作用的介质最后才到达地球的 。
推荐阅读
- 科学家发现记忆和灵魂的秘密,以前的研究全是错的?
- 科学家发现试管婴儿更聪明?诺奖得主发文,智力发展源自于多种因素
- 人被砍头后,还有疼痛感吗?法国科学家亲身试验,用生命得到答案
- 现实中发现计算机代码,科学家认为世界是虚拟的几率为百分之百
- 人类并不是宇宙唯一生命,科学家发现超级地球,认为百分百存在生命
- 月球上没有火箭和发射塔,美国人如何做到返航?科学家:搭顺风车
- 疯狂的“人兽杂交”!前苏联做过实验,让5名女性和黑猩猩生孩子
- 科学家在沿海海床下发现蔗糖堆,并表示:一旦分解,后果很严重的
- 沉睡冰川的远古病毒,终将与人类跨时空一战,赤道将成为胜负手







