
文章图片

文章图片
文章图片
关于光速的问题 , 始终是人们津津乐道的话题 , 因为光是大家生活中常见的一种物质 , 而按照狭义相对论 , 光线传输也是宇宙中运动速度最快的现象 , 如果能以光的速度行进 , 则在其所处的惯性参照系中 , 将产生一系列奇妙的结果 , 这里面的时间膨胀效应尤为受到人们的关注 , 催使人们形成了各种各样的疑问 , 今天我们就来分析一下如果能够驾驶一个接近光速飞行的飞船 , 在飞行一分钟后返回地球 , 地球在此过程中时间流逝的问题 。
爱因斯坦在提出狭义相对论时 , 有两个基本的假设前提 , 其中一个就是著名的光速不变原理 , 即在所有的惯性参照系中 , 观察光线在真空中的传播速度 , 都将保持着一个恒定的数值 , 即30万公里每秒 , 这个数值不会因观测者所处的是哪一个惯性参照系而改变 , 也不会因观测者、目标物体的移动而改变 , 只要满足惯性参照系的条件即可 。
根据狭义相对论中关于运动的表述形式 , 我们可以看出任何一个物体 , 在一个惯性参照系中的运动 , 都会对所处的时间和空间产生一定影响 , 物体的运动速度不同 , 这种影响程度也会不同 , 也就是说在不同的惯性参照系内来进行观测 , 那么由于物体的运动所造成的时空改变不具有一致性 。 根据洛伦兹变换 , 我们可以用数学的方式来描述物体的运动 , 对于时间和空间改变的影响 。
从物体与观测者之间的相对运动来看 , 在两个惯性参照系下 , 物体的不同运动速度之间 , 存在着如下的对应关系 , 即:v/u=1+(1-v^2/c^2)^(1/2) , 这个关系式不同于经典动力学中的伽利略变换 , 后者只是单纯的数值累加 , 相对论条件下 , 物体的运动“叠加”速度 , 既与在一个惯性参照系下的“初始”速度有关 , 也与光速有关 , 无论这个物体在惯性参照系下的运动速度有多快 , 其最终的“叠加”速度都不能超过光速 。 这也是为什么理论上两个相向而行的光线 , 从一个光线上看另一个光线的运动速度也是光速c、而不是2倍c的原因 。
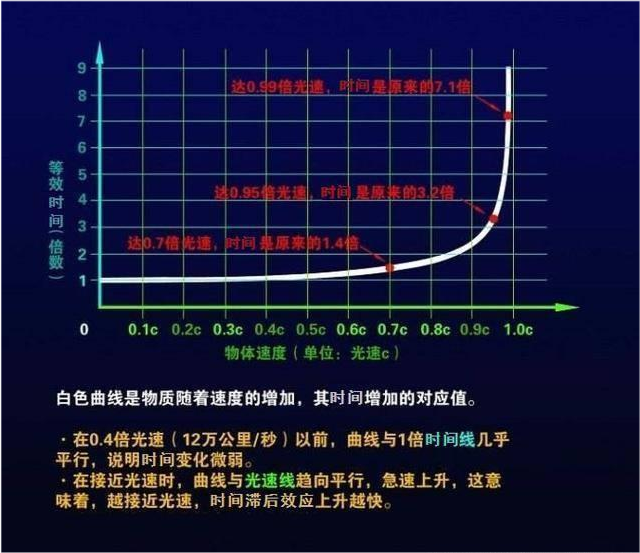
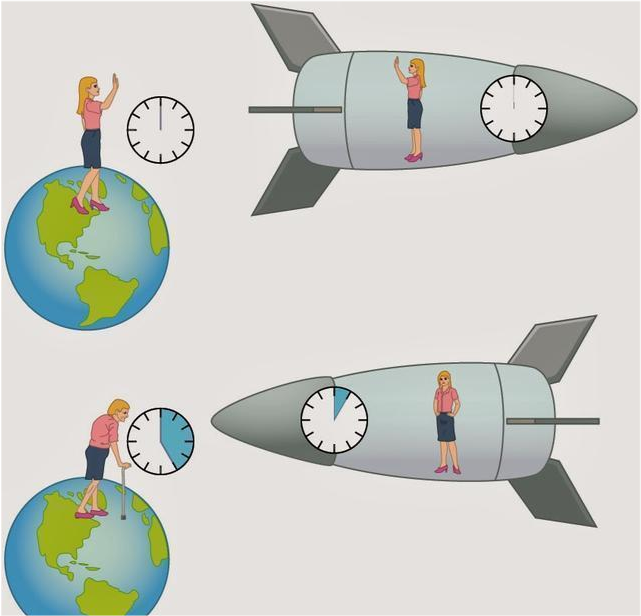
在此基础上 , 可以得出狭义相对论下的两个著名推论 , 一个是尺缩效应 , 另一个是钟慢效应 , 它们分别对应的是在高速运动状态下 , 在不同惯性参照系内 , 物体移动所通过空间距离以及时间流逝的差异 。 拿钟慢效应来说 , 处于两个惯性参照系内的时间流逝速度之比为:T’=T*(1-v^2/c^2)^(1/2) , 通过这个公式我们可以看出 , 飞船的运动速度越快 , 在飞船所在的惯性参照系内观察时间流逝速度虽然正常 , 但对于从地球等其他并未发生明显位移的惯性参照系内来看 , 飞船上的时间流逝速度越来越慢了 , 反过来觉察地球上的时间流逝速度要比飞船上得快 。
以上就是钟慢效应产生的原因 , 它所表达的是两个惯性参照系内时间流逝速度的对应关系 , 无论是从观测者来说 , 还是在光速飞船上的人来说 , 它们本身处在的惯性参照系内的时间流逝 , 分别是两个独立的过程 。 如果它们之间没有信息联系的话 , 那么从地球上看飞船上的人 , 感觉飞船上的时间过得慢甚至停滞 , 那么反过来一样成立 , 地球相对于飞船也处于光速运行 , 那么光速飞船上的人看地球上的人 , 一样也是感觉他们时间过得慢甚至停滞 。 这样就会产生一个悖论 , 那就是如果以光速飞船飞行一段时间后 , 到底是谁变“老”了呢?
【如果驾驶亚光速飞船,飞行一分钟后再返回地球,还能见到家人吗?】要解释这个问题 , 还得明确一个概念 , 这也是狭义相对论中反复强调的问题 , 那就是相对论成立的条件 , 必须是在惯性参照系内 , 即两个参照系物体的运动 , 必须是处于静止或者匀速运动的状态 , 如果在任何的一个参照系发生加速或者减速 , 那么无论是空间还是时间的相对性都会发生改变 , 就不会再适用狭义相对论了 。 如果以光速飞船离开地球之后不再回来 , 那么无论是从哪个参照系来看 , 它们的时间流逝速度都是相互独立且不互相影响 , 也就是不发生信息交流 , 地球上的人、飞船上的人该怎么着还是怎么着 , 没有什么对比产生 。
推荐阅读
- 依据质能方程,可以将质量转化为能量,能否用能量生成1g的质量?
- 宇宙整体上会是什么样的一个形状?
- 2019年,男子酒后骑行撞墙死亡,死者家属:外墙违章应该赔偿
- 为什么近百年来,物理学似乎一直在停滞不前,没有重大突破了?
- 物理学停滞100年,三座大山一直在阻碍!解决任何一个将改变人类
- 大妈赖在出租车7小时,在副驾驶小便三次,大妈: 给5000我就下车
- 暗能量造成宇宙加速膨胀?量子引力模型的引入,让结果更扑朔迷离
- 乘坐无限接近光速的飞船飞行,你的时间就静止了吗?
- 量子阱太阳能电池的效率几乎达到创造世界纪录的“40%”






