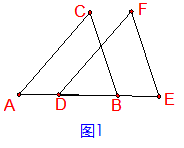
1、已知:如图1 , 点A、D、B、E在同一条直线上 , AD=BE,AC∥DF,BC∥EF.
文章图片
求证:AC=DF.
思路分析:要证明AC=DF , 则需要证明⊿ABC≌⊿DEF.在⊿ABC和⊿DEF中 , 由AC∥DF可得∠CAB=∠FDE, 由BC∥EF可得∠CBA=∠FED,现已证两三角形的两组对应角相等 , 所以考虑夹边 , 用ASA , 证明⊿ABC≌⊿DEF.由已知AD=BE可得:AD+DB=BE+DB,即AB=DE , 命题得证.
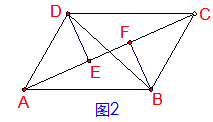
2、已知:如图2 , BE⊥AC,DF⊥AC,垂足分别是E、F,O是BD的中点.
文章图片
求证:BE=DF.
思路分析:要证明BE=DF , 则需要证明⊿BOE≌⊿DOF.在⊿BOE和⊿DOF中 , 由BE⊥AC,DF⊥AC可得∠BEO=∠DFO=90°,∠BOE=∠DOF,现已证两三角形的两组对应角相等 , 所以考虑其中一组对应角的对边 , 用AAS , 证明⊿BOE≌⊿DOF.由已知O是BD的中点可得:OB=OD , 条件已具备 , 命题得证.
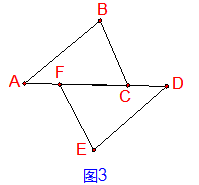
3、已知:如图3 ,AB=DE,BC=EF,AF=CD.
文章图片
求证:AB∥DE, BC∥EF.
思路分析:要证明AB∥DE, BC∥EF , 则需要证明∠A=∠D, ∠BCA=∠EFD,由此只需要证明⊿ABC≌⊿DEF.在⊿ABC和⊿DEF中 , 已知AB=DE,BC=EF,即两三角形的两组对应边相等 , 因此 , 只需证明边AC=DF , 用SSS证明⊿ABC≌⊿DEF.由已知AF=CD ,根据等式性质得:AF+CF=CD+CF,即AC=DF , 命题得证.
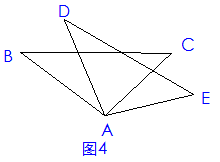
4、已知:如图4 ,AB=AD,AC=AE, ∠BAD=∠CAE.
文章图片
求证:. ∠B=∠D.
思路分析:要证明∠B=∠D , 只需要证明⊿ABC≌⊿ADE.在⊿ABC和⊿ADE中 , 已知AB=AD, AC=AE,即两三角形的两组对应边相等 , 因此 , 只需证明两条已知边的夹角相等 , 用SAS证明⊿ABC≌⊿ADE.由已知∠BAD=∠CAE ,根据等式性质得:∠BAD+∠DAC =∠CAE+∠DAC , 即∠BAC=∠DAE , 命题得证.
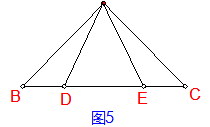
【初二|初二数学下册:第十七章勾股定理同步训练】5、已知:如图5 ,AD=AE,点D、E在BC上 , BD=CE,∠ADE=∠AED.
文章图片
求证: ⊿ABE≌⊿ACD
思路分析:要证明⊿ABE≌⊿ACD , 在⊿ABE和⊿ACD中 , 已知AD =AE, ∠ADE=∠AED即相邻的一角一边对应相等 , 因此 , 只需证明∠ADE与∠AED的另一邻边相等即可 , 用SAS证明⊿ABE≌⊿ACD.由已知BD=CE可得:BD+DE=CE+DE,即BE=CD , 命题得证.
end
声明:本文内容来源于网络 , 转载请联系原出处 。初三研究中心尊重版权 , 如有侵权问题 , 请及时与管理员联系处理 。
点击 "阅读原文" 加 中考君微信好友哦
推荐阅读
- 直线|初一数学下册:平移知识点整理
- 人物|大学生为返校从山东骑车10天到上海:初二就出发了
- 杰尔·希钦|粒子物理学有了新的基础数学理论
- 奥地利|粒子物理学有了新的基础数学理论
- 直线|初一数学下册:平行线的性质相关知识点
- 勾股定理|初二数学下册:第十七章勾股定理知识点总结
- 艾伦·佩利|不想当数学家的化学家,是搞不好计算机的!——首位图灵奖得主艾伦·佩利的开挂人生丨图灵宇宙
- 人物|知名投资人聊天群内自曝从小培养儿子做渣男 初二就有俩女友
- 同类|初二数学下册:二次根式的加减知识点汇总
- 相关|2022年沃尔夫数学奖得主公布





