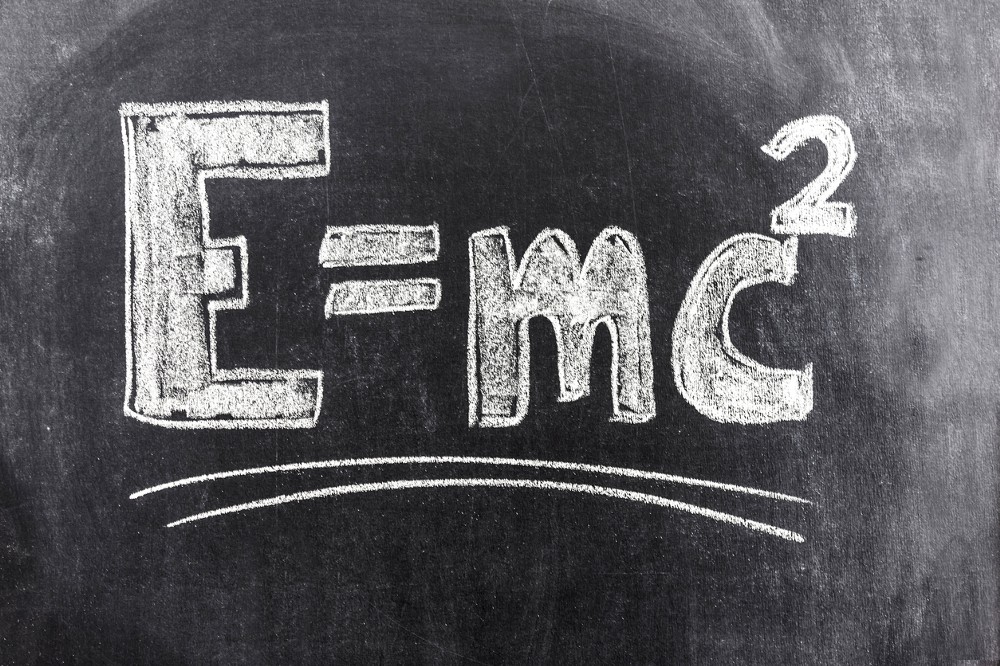
物理学中最重要、最美丽的五个基本方程，“导致”很多伟大的发现 _美丽

文章图片

文章图片

方程是最美丽的数学表达式，它展示和解释了宇宙的物理现实。从勾股定理到薛定谔方程，它们都在物理学中起着至关重要的作用，特别是因为它们把一个物理量和另一个物理量联系起来，这意味着一个物理量或参数的改变也会引起其他物理量或参数的改变。
物理学家们多年来一直在努力寻找并构建一个单一的方程，通过结合量子力学和相对论来解释宇宙的所有物理现象，卡库道夫博士称其为“上帝方程” 。在这里，我们将讨论物理学中使用的五个最重要（也是最漂亮）的方程。这些方程式被科学家们用来描述宇宙中一些最美丽的现象，并导致了许多其他伟大的发现。

我们可以把电，磁和引力归纳成一英寸长的方程，这就是场论的力量。所以我对自己说：我要创造一个弦的场论。有一天，当我这么做的时候，我感到不可思议，我意识到在一张纸上我可以写下一个等式，它概括了几乎所有的物理知识。

【物理学中最重要、最美丽的五个基本方程，“导致”很多伟大的发现】牛顿第二定律

牛顿第一运动定律预测了物体的运动。第一定律有时被称为惯性定律，如果作用在物体上的力是平衡的，那么这个物体的加速度将是0米/秒/秒。
牛顿第二运动定律适用于那些并非所有力都处于平衡状态的物体。第二定律指出，物体的加速度取决于两个变量——作用在物体上的合力和物体的质量。
F = ma ，其中F是力， m是质量， a是加速度，尽管它看起来很简单，但它不断给研究它的人带来新的见解。它被低估的部分原因是因为它无处不在，如果你要学习物理，你就要学习牛顿，而这个方程就是牛顿第二定律的核心。
质能关系方程

爱因斯坦的质能等效关系也许是最著名的物理（科学）方程，它解释了为什么核反应会产生巨大的能量。这方程式展示了质量如何转化为能量，反之亦然。 E = mc^2所表示的光、质量和能量之间的关系是，我们所认为的“物质”是以某种方式被“囚禁”的密集的能量，物质与“纯”能量的区别在于它具有半整数自旋，即费米子物质。
狄拉克方程

狄拉克方程是英国物理学家保罗·狄拉克于1928年提出的相对论波动方程。本质上，他提出这个方程是为了纠正他所看到的量子力学和狭义相对论之间的冲突，这两个理论各自都非常成功。在方程中， ψ是某个自旋1/2粒子的波函数。狄拉克方程帮助我们理解宇宙中存在的物质以及物质的行为。
狄拉克方程是电子的相对论性描述。电子的非相对论性描述可以用泡利-薛定谔方程来描述。非相对论电子有两个自旋态，我们说它是一个二分量方程。狄拉克证明了没有两个分量的泡利-薛定谔方程的相对论版本，而最小的相对论类似物是一个四分量方程。狄拉克方程中附加的其他分量（或自由度）是反粒子的状态。
爱因斯坦场方程

这个方程预测了在质能存在的情况下四维时空是如何弯曲的。它解释了引力的作用，并在弱曲率极限下再现了牛顿引力平方反比定律。它预测了黑洞的存在和性质，并适用于整个宇宙。例如，这个方程决定了宇宙从大爆炸到现在的几何形状，并将适用于遥远的未来。例如，宇宙常数就是暗能量的一个可能模型。
这些方程最初是由阿尔伯特·爱因斯坦在1915年发表的，它将时空的几何形状与其中物质的分布联系起来。在方程中