Descent|NeurIPS 2020 | 求解对抗训练等Min-Max问题的简单高效算法
?作者:香港中文大学 (深圳) 五年级博士生 张佳玮
伊利诺伊大学厄巴纳-香槟分校四年级博士生 肖佩君
NeurIPS 2020 文章专题
第·6·期
本文将分享 香港中文大学 (深圳) 和 伊利诺伊大学厄巴纳-香槟分校合作发表于NeurIPS 2020的工作: 《求解非凸-凹Min-Max问题的单环平滑梯度下降-上升算法》 。
Min-Max问题 , 也称极小-极大问题或者极小极大化 , 是一类常见且重要的数学规划问题 。 此类问题是为了找出失败的最大可能性中的最小值 , 在经济、工程、统计等领域中有广泛的应用 。 像两人博弈中的零和问题 , 就能写成一个极小-极大问题。
在机器学习领域 , 我们也经常需要求解极小-极大问题 , 比如热门的对抗训练和生成对抗网络 。 梯度下降-上升 (Gradient Descent Ascent, GDA) 算法是解极小-极大问题的常用方法 , 但对于非凸问题而言 , 在用固定的步长的情况下 , GDA算法不能保证收敛 。
本文对 GDA算法使用了“光滑化”的技巧 , 使得算法可以收敛 , 且在非凸-凹的极小-极大问题的两类常见形式上 , 可以达到目前最优的收敛性结果 。在实验中 , 该工作在分类问题的对抗训练中使用了光滑化GDA算法 。 结果显示 , 光滑化GDA算法可以更高效地收敛 , 并达到很高的对抗正确率 。
文章图片
https://arxiv.org/abs/2010.15768
一、研究问题
对于一个函数 f(x,y) , 假如它对于 x 这个变量是非凸的 , 那我们称
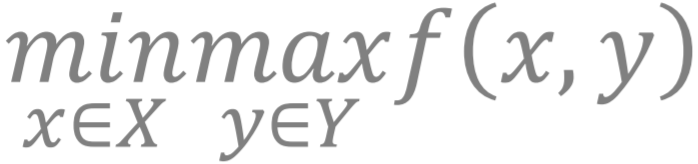
文章图片
这个问题为非凸极小-极大问题 , 其中 X 和 Y 分别是两个问题变量 x 和 y 的定义域 , 他们都是凸的闭集 。 我们先介绍两个实际例子 。
1.1 实际例子
例子1:在多个分布上的鲁棒训练 。 在机器学习中 , 我们通常会假设不同的数据集来源于多个分布 。 假设我们有 n 个数据集 , 它们对应的分布为

文章图片
, 每一个分布
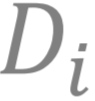
文章图片
都是对真实的数据分布
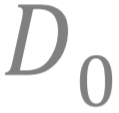
文章图片
进行不同的扰动而得到的分布 。
假设我们要训练的参数是 x, 关于数据样本 a 的损失函数是 F(x ; a), 鲁棒训练的目标是尽可能减少在不同分布上最坏损失函数的值 。 具体来说 , 鲁棒训练可写成以下极大-极小优化问题:
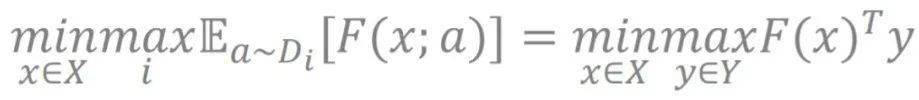
文章图片
其中 , Y 是一个概率单纯形 ,
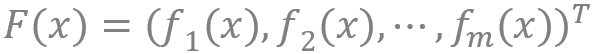
文章图片
,
且

文章图片
是在分布
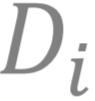
文章图片
上的期望损失 。在对抗学习的文献中 , 分布 是第 i 个攻击者生成的对抗样本 。 这是下面会讲到的 形式2的一个实际例子 。
例子2:训练公平的模型 。 在机器学习中 , 我们有可能会训练出不公平的模型 , 具体来说 , 一些模型可能会根据个体在某些类别中的成分来做出不利于或者歧视此个体的判断 。 比方说 , 一个用来预测个人薪水的算法 , 可能会用个体的一些特殊特征 , 诸如性别、种族和肤色 , 来进行预测 , 这会带来不公平的结果 。 要训练出公平的模型 , 其中一种方法是考虑解以下这个优化问题:
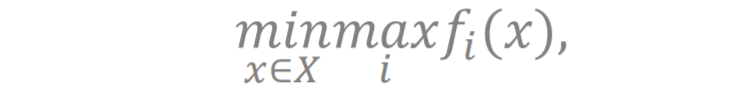
文章图片
其中 x 是模型的参数 ,
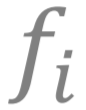
文章图片
是对应不同的类别的损失函数 。 这是下面会讲到的 形式1的一个实际例子 。
1.2 非凸-凹问题的一般形式和特殊形式
前文我们给出了非凸极小-极大问题的形式 , 当我们进一步限制函数 f(x,y) 关于问题变量 y 是一个凹函数 , 那我们就称

文章图片
为非凸-凹极小-极大问题的一般形式(后面简称为“一般的非凸-凹问题”)。
在最一般的情况中 , Y 可以是任何闭集;在现实中 , 我们经常会遇到以下两种特殊的 Y (这两种问题实际上是等价的) :
形式1:离散的问题 。 Y 是一个离散集合 [1, 2, … , m] , 而 是 m 个不同的关于 x 的函数 。 更具体地说 , 对每个固定的 x, 我们对有限个非凸函数

文章图片
取最大者 , 得到一个函数
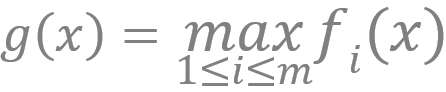
文章图片
,
然后求g(x)的最小值
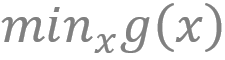
文章图片
, 这个问题可以写成
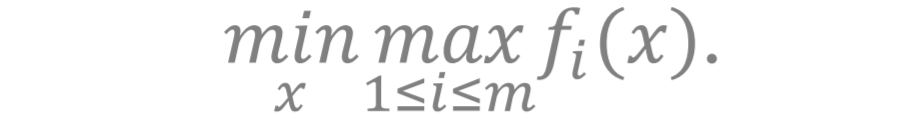
文章图片
形式2: 连续的问题 。 Y 是一个概率单纯形 , 即

文章图片
且定义
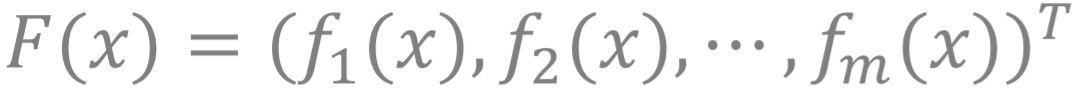
文章图片
,
得到如下的问题
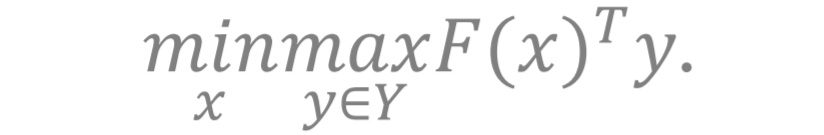
文章图片
细心的读者可以发现 , 前文提及的两个例子都能写成这两个常见的等价形式中的其中一种 。 比如 , 例子1里的在多个分布上的鲁棒训练就是形式2的一个实际例子 ,而例子2中的公平训练问题是形式1的实际例子 。
二、已知结果与挑战
2.1 从最基础的GDA讲起
我们首先回顾一下解决极小极大问题的常见算法:梯度下降-上升 (Gradient Descent Ascent, GDA) 算法 。 要解释GDA算法 , 我们先回顾常见的求极小问题
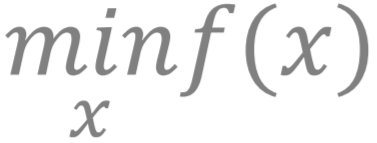
文章图片
, 梯度下降算法 (Gradient Descent, GD) 是在每一次迭代中 , 对参数 x 沿着梯度相反的方向前进一个步长 。 类似地 , 梯度上升算法 (Gradient Ascent, GA) 是为了解决求极大问题 , 在每一次迭代中 , 对参数 x 沿着梯度的方向前进一个步长 。 而梯度下降-上升 (Gradient Descent Ascent, GDA) 算法就是对优化问题中的极小问题先做一次梯度下降 , 再对极大问题做一次梯度上升 。 以下是GDA算法:

文章图片
GDA是典型的单环迭代算法 。 此处单环的意思是 , 这个算法每一次迭代只需要一个内循环即可 。 我们已知对于非凸-强凹极小极大问题 (此处函数 f(x,y) 关于 y 是强凹的), 最基础的单环迭代算法——GDA算法就可以做到以
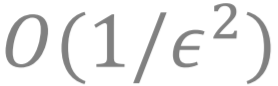
文章图片
的迭代复杂度找到一个 ? 数量级的近似解 。
2.2 已知的结果
我们想知道的是:对于非凸-凹极小极大问题 (此处函数 f(x,y) 关于 y 不要求是强凹的), 能否设计算法可以同样达到
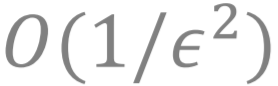
文章图片
的迭代复杂度?
可惜的是 , 目前已知的算法无一能达到

文章图片
的迭代复杂度 。 已知的结果可分成两类:一种像GDA这样的单环迭代算法 , 一种是双环甚至三环迭代的算法 。 双环 (或三环) 迭代算法是指每一次迭代需要做两 (或三) 个内循环 。 双环 (或三环) 迭代算法比单环迭代算法更为复杂 。
我们先了解一下已知的单环迭代算法的缺点 。 我们在引言里就提到 , 单环迭代算法的代表——GDA算法在解决非凸-凹极小极大问题时 , 若使用固定的步长 , 则有可能会不收敛 。 近年来有研究者提出基于GDA的单环算法 , 但是这些算法都需要用递减的步长才能保证收敛 。 而用递减的步长 , 无疑会减低收敛速度 , 使得此类算法难以达到 的迭代复杂度 。
目前最好的结果都是用多环迭代算法达到的 , 最好能到
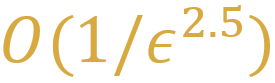
文章图片
的迭代复杂度 。 多环迭代算法也有自身的缺点 , 它们更复杂 。 因为有多层内循环 , 所以他们比单环迭代算法拥有更多的超参数 , 从而增加调试超参数的难度 。 另一个缺点是 , 因为复杂的多环结构 , 我们较难把多环迭代算法拓展到多个变量块的设定 (multi-block setting) 。 也就是说 , 我们难以把高维度的问题变量拆分成多个变量块分配到不同的机器上 。 最后一个缺点 , 从理论角度来说 , 最严重的缺点是:多环迭代算法几乎不可能达到 的迭代复杂度 , 它们每一次迭代的最外环计算就已经需要 的迭代复杂度来保持足够的精度 , 而内环的计算复杂度也与 ? 有关 , 因此复杂度严格比 更差 。
小结一下 , 在已知的结果中:
我们面对的挑战是 , 如何找到一种算法 , 同时具有上述两类方法的优点 , 既有较高的收敛速度 (比如达到
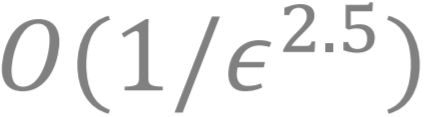
文章图片
的迭代复杂度), 且具有单环迭代算法的简单性?更进一步 , 如果这个算法还能拓展为多块分布式算法 (以解决大规模问题) 就更好了 。 下面我们将介绍这个问题的解决方法 。
三、光滑化GDA算法
我们分三步来设计出可行的算法 。 先从最基础的GDA算法开始 。
第一步:我们需要使用一个新的变量 z 来对原有的变量 x 进行辅助 。 具体来说 , 在每一个迭代时刻 t, 对于每一个

文章图片
,我们都有对应的一个指数加权移动平均变量
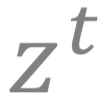
文章图片
。
第二步:因为多了新的变量 z, 我们需要引入一个新的函数 K(x, z ; y) 来平衡 x, y, z 三个变量之间的关系 。 具体来说 , 我们希望这个辅助变量 z 与原来的变量 x 不会太远 , 且我们还是在解决原来关于 f(x,y) 的极小极大问题 。 基于这样的思想 , 我们设定 K(x, z ; y) 为原来的函数 f(x,y) 加上一个约束 x 和 z 的关系的二次项 。
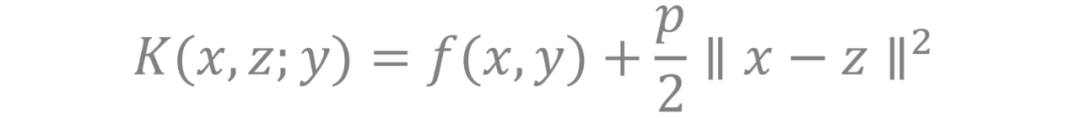
文章图片
第三步:我们把第一步和第二步组装起来:对新的函数 K(x, z ; y) 做 GDA 算法来更新 x 和 y , 然后通过光滑化来更新变量 z。 这就得到了光滑化GDA算法!

文章图片
值得注意的是 , 我们的光滑化GDA算法使用固定的步长 。 另外 , 很容易把它推广到多个变量块的设定 , 见下图的推广算法 。 我们把 x 分成 N 个变量块 , 在更新 x 的时候 , 对逐个变量块进行逐步更新 (类似于交替最优算法 alternating minimization)。 这个算法可以被应用在分布式的系统中来解决大规模的问题 。

文章图片
四、理论结果
我们提出的光滑化GDA算法以及其对多个变量块的设定的拓展算法 , 在前文提及的两个特殊形式的问题上 , 都可以达到
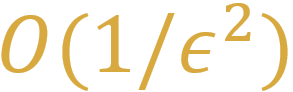
文章图片
的迭代复杂度 , 这是目前最优的结果。 我们将该算法与其他已知算法的对比总结到下面的表格中 。 下表中 “Smoothed-GDA” 对应本文算法 , 可见复杂度是目前最优 , 且是简单的单环结构 , 并且能拓展到多变量环的设定 。

文章图片
另外 , 在一般的形式中 , 我们可以达到

文章图片
的迭代复杂度 , 这个结果与 [Lu et at., 2019] 的结果一样 , 他们同样是用单环迭代算法 , 但我们的文章和该文相比有两点区别:第一 , 我们的算法在前面提到的常用形式上可以达到 的迭代复杂度;第二 ,我们的结果不需要像 [Lu et at., 2019] 一样假设 X 是紧集 。
五、实验表现
为了测试光滑化GDA算法 , 我们考虑对抗训练问题 。 我们使用MNIST和CIFAR10数据集 。 下图是MNIST数据集上不同算法在不同的扰动强度下的准确率 。 结果显示光滑化GDA算法的对抗正确率高于其他算法 。
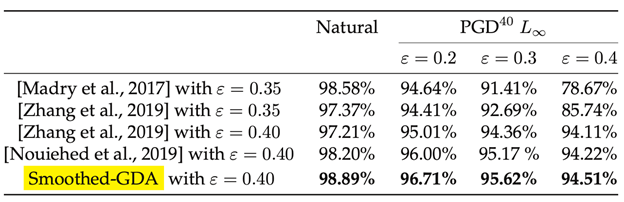
文章图片
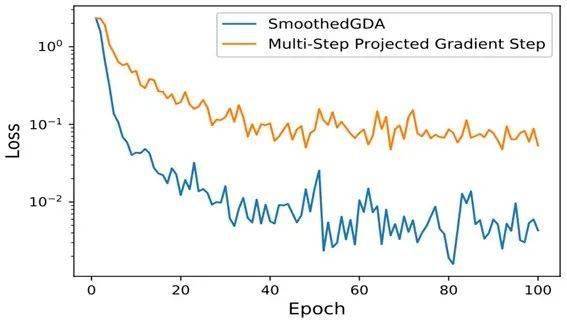
下图是将光滑化GDA算法的收敛曲线与一个双环迭代算法做比较 。 结果显示光滑化GDA算法收敛速度更快 。
我们接着在CIFAR10分类问题上也作对抗训练 , 同样观察到光滑化GDA算法类似的优异表现 。
文章图片
【Descent|NeurIPS 2020 | 求解对抗训练等Min-Max问题的简单高效算法】六、总结与展望
本文考虑了非凸-凹的极小-极大问题 , 提出了一个光滑化GDA算法 。 这个算法能以
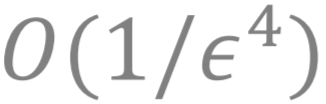
文章图片
的迭代复杂度找到一个 ? 数量级的近似解;更重要的是 , 对于实际中常见的一类特殊形式问题 , 光滑化GDA算法能以 的迭代复杂度得到一个 ? 数量级的近似解 , 这个收敛性速度结果是目前最优的 。
我们把光滑化GDA算法推广到多个变量块的设定上 , 可应用在分布式的系统中来解决大规模的问题 。 在分类问题的对抗训练中 , 光滑化GDA算法收敛速度高于其他多环GDA算法 , 并取得了更高的对抗正确率 。 在以后的工作中 , 我们希望结合神经网络结构 , 提出针对神经网络训练的更高效算法 。
//
作者介绍:
张佳玮 , 香港中文大学深圳罗智泉教授实验室五年级博士生 , 此前于2016年在中国科学技术大学华罗庚数学班获得学士学位 , 他目前的研究兴趣是优化理论及其在机器学习和信号处理中的应用 。
肖佩君 , 伊利诺伊大学厄巴纳-香槟分校孙若愚教授实验室四年级博士生 , 此前于2017年在加州大学戴维斯分校数学系获得学士学位 , 她目前的研究兴趣是优化理论及其在机器学习的应用 。
推荐阅读
- 平板|小新 Pad Pro 2020 平板开启 OTA7 ZUI 13 灰度推送
- 国际|特奖得主任队长,清华夺冠NeurIPS 2021国际深度元学习挑战赛
- 国际|2020年我国产出卓越科技论文46万余篇
- 排名|2020年我国国际顶尖期刊论文数量排名世界第二 上升2位
- 最新消息|印度创企2021年获360亿美元投资 比2020年增长2倍
- 未来|汾酒荣获2020年度中国食品工业协会科学技术奖两项殊荣
- the|美国疾控中心公布2020年十大死因:心脏病排名第一 癌症第二
- the|CDC:美国人均预期寿命在2020年缩短近2年
- 疫情|中科院报告:2020年中国共出版科普图书近亿册
- 期刊|中国首部科学传播报告:2020年出版科普图书9853.6万册





