珠峰高程测量 , 从登顶成功测量 , 到最终的数据公布 , 历时有半年多 , 为什么需要这么长时间 , 计算珠峰高度都有哪些困难?
在陕西地理测绘信息局的办公大楼里 , 大地测量数据处理中心 , 就是处理此次珠峰高程测量所有数据处理分析的一个机构 。 实际上早在2005年 , 当时珠峰到底有多高 , 这个数据也出自于这里 。

文章图片
相比于2005年 , 此次大地测量数据处理中心所面对的数据来源更为丰富、数据量更大 , 包括水准测量、全球导航卫星系统测量、三角高程测量、航空与峰顶重力测量以及雪深雷达测量等多种数据 。 其中 , 全球导航卫星系统测量中首次采用我国自行研制的北斗卫星导航系统 , 卫星观测数量就多达20多颗星 。

文章图片
央视采访人员 杨潇:数据处理中心里 , 实际上并不是所有的人都在围绕珠峰高程测量这一项工作 , 处理这项工作的只有五个像这样的数据处理工作室 , 一个数据处理室将近8个人而已 , 他们所要面对的是海量的处理数据 。
文章图片
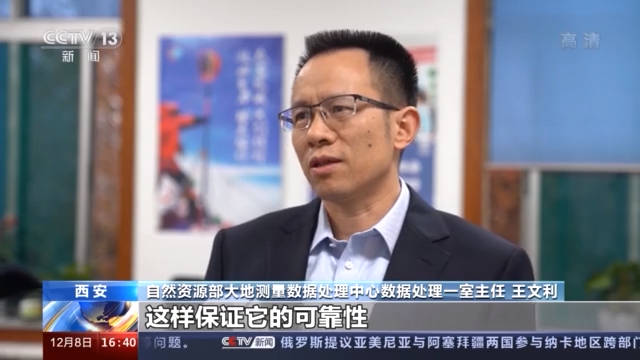
自然资源部大地测量数据处理中心数据处理一室主任 王文利:处理的数据量 , 光测角测边的数据就是将近上万条 , 而且咱们这个数据 , 基本上这一次全是手工记录的 , 因为它这种测角测边 , 在各个交汇点上 , 它是经过了三天 , 测了三天才测出来 , 每一个点 , 它要测将近100个测绘 , 有些那个角度测几十个测绘 , 这样保证它的可靠性 。
文章图片
此次珠峰高程测量 , 既用了传统测绘技术 , 也用了综合现代测绘技术 , 所以需要处理的数据量非常大 , 技术人员要在采集分析的基础上 , 还要通过多种程序进行不断的演算 。 比如 , 为了拿出一个准确的大地水准面模型 , 技术人员就先后做了3000多钟方案 。

文章图片
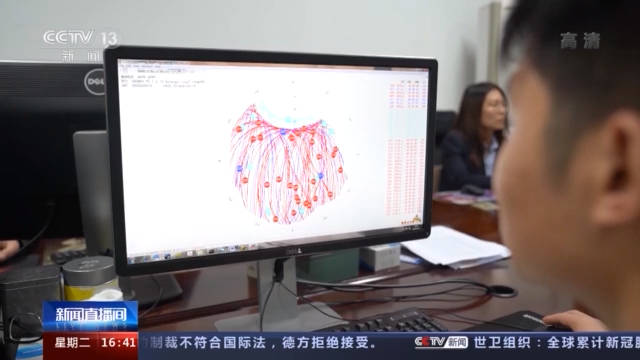
自然资源部大地测量数据处理中心数据处理四室主任 刘晓云:这个是比较花时间的 , 因为要准备重力数据、地形数据 , 数据量都是非常大的 , 然后再去基于不同的重力场模型 , 不同的积分半径算出3000多种模型 。
文章图片
在计算过程中 , 技术人员还发现 , 此次珠峰高程测量 , 汇总来的数据精度之高 , 全面体现了中国测绘的最高水平 。

文章图片
自然资源部大地测量数据处理中心主任 郭春喜:我们的数据量增多了 , 我们测的东西更加可靠了 , 也就是从测绘说的话 , 它的精度提高的比较大 。 简单说 , 就是说我们原来一个很重要的高度 , 就是峰顶的大地高的精度 , 2005年的是3个厘米 , 我们这次是9个毫米 , 说明啥意思 , 它的精度是在提升 。 就说明我们国家整个大地测量的技术水平应该说具有国际的先进水平 。
我国测绘工作者之前曾多次测珠峰
新中国成立以来 , 我国测绘工作者分别于1966年到1968年、1975年、2005年对珠峰进行过多次大规模的测绘和科考工作 。
1966到1968年 , 我国两次对珠峰地区进行了大规模的测量 。 但测得的高度并未对外公布 。1975年5月27日 , 我国科考队员首次将测量觇标设立在珠峰峰顶 , 最终精确得到珠峰高度为8848.13米 。 1975年7月23日 , 我国向全球宣布了珠穆朗玛峰的海拔高程 。2005年5月22日 , 我国登山测量队员再次登顶珠峰 , 并在峰顶启动雪深雷达探测仪 , 探测珠峰顶峰的冰雪厚度 , 为3.50米 。 2005年10月9日 , 我国向全世界公布:珠穆朗玛峰峰顶岩石面海拔高程为8844.43米 。
今天 , 中尼两国联合宣布 , 经过两国团队的扎实工作 , 珠穆朗玛峰的最新高程为8848.86米 。
独家专访党亚民:珠峰“长高”的背后
今天中尼两国联合对外公布的珠峰新高程为8848.86米 , 相比以前公布的高度 , 珠峰“长高”了一点 , 为什么会有这个差异?中尼珠峰测量联合技术委员会主席党亚民接受总台央视采访人员的独家专访时表示 , 珠峰的高度处于一个上升的趋势 , 在合理的区间范围内 。
党亚民表示 , 实际上珠峰的高度逐年都发生着变化 。 珠峰地区乃至整个青藏高原 , 都是印度板块和亚欧板块碰撞挤压而成 。
文章图片
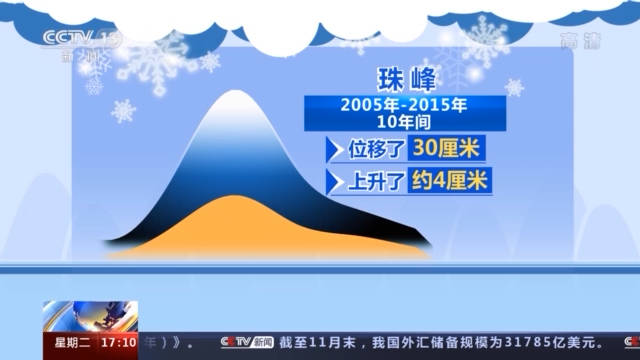
在千百年的岁月里 , 挤压一直在进行中 , 所以珠穆朗玛峰的高度每年都会发生变化 。 相关数据显示 , 2005年至2015年10年间 , 珠峰地区以每年约3厘米的速度向东北方向移动 , 以每年约0.4厘米的速度上升 , 也就是说珠峰在10年位移了30厘米、上升了约4厘米 。
文章图片
中尼珠峰测量联合技术委员会主席 自然资源部中国测绘科学研究院研究员 党亚民:我们的珠峰数据处理团队 , 在数据处理过程中 , 也做了一些研究 , 应该说整体趋势上来说 , 我们这一次珠峰的(高程)应该是略微变高 , 变高的也不是说变的超乎大家的想象 , 就是在一个合理的范围之内 。

文章图片
党亚民介绍 , 根据长期对珠峰的观测来说 , 它也是一个上升的趋势 , 所以比之前的数据长高了一点 , 也在情理之中 。 还有就是这次珠峰测量的精度进一步提升 , 采用了GNSS卫星测量、精密水准测量、雪深雷达测量、卫星遥感等多种传统和现代测绘技术 。 特别是进行了全球首次航空重力测量 , 海拔高起算面更加精确 。

文章图片
中尼珠峰测量联合技术委员会主席 自然资源部中国测绘科学研究院研究员 党亚民:我们这一次引入了航空重力数据 , 还有一些新的数据使起算面的精度大幅度的提高 , 提高的结果 , 也就是起算面比以前可能要低了一点点 , 就是在你量身高的时候 , 相当于底下起算面低了 , 你肯定人就变高了 。珠峰海拔高包括峰顶雪面高度
这次公布的珠峰高程数据是8848.86米 , 是包含珠峰峰顶雪面的高度 , 不是岩石面高度 , 对此党亚民表示 , 雪面高是中尼双方共同认可的结果 。
中尼珠峰高程测量的总体目标是两国共同宣布珠峰高程数据 , 而雪面高是双方共同认可的结果 。

文章图片
中尼珠峰测量联合技术委员会主席 自然资源部中国测绘科学研究院研究员 党亚民:我们每次进行珠峰高程测量的时候 , 队员登上最高的峰点 , 然后就开始测量 , 找到最高的雪面的这么一个最高点 , 我们就在这个点上进行测量 。 而且现在的我们的测绘技术可以把这个点的高度测得特别准 , 这个结果就容易被大家认可 。

文章图片
党亚民表示 , 除此之外 , 此次珠峰高程测量有一些特殊性 , 2019年尼泊尔就完成了峰顶测量 , 而我国今年5月27日完成了峰顶测量 。 大家都知道 , 珠峰峰顶气候条件恶劣 , 10级以上的大风是常有的事 , 这样一来 , 峰顶雪面高是有变化的 。

文章图片
中尼珠峰测量联合技术委员会主席 自然资源部中国测绘科学研究院研究员 党亚民:所以我们两国的科学家也进行了反复的研究 , 这个问题怎么来解决 。 后来我们认为把两个国家分别测量的雪面高度经过数据的融合处理 , 根据一定的原则 , 取一个平均是一个比较合理的结果 。
精确测定意义重大
为什么要精确测量珠峰高程?对我国乃至世界有什么重要意义呢?党亚民表示 , 最新发布的珠峰高程数据 , 可以为全球气候变化、冰川监测、生态环境保护等方面的研究提供第一手资料 。
专家表示 , 珠峰高程的精确测定 , 可以结束国际上珠峰高程不统一的混乱局面 , 为世界地球科学研究作出贡献 , 其社会效益和科学意义是十分巨大的 。

文章图片
中尼珠峰测量联合技术委员会主席 自然资源部中国测绘科学研究院研究员 党亚民:那么(中尼)两个国家的相关的主管部门是有责任有义务精确测定出来 , 然后以国际合作的形式共同宣布 , 对于两国的人民也是一个非常重大的一个事情 。 同时我们两国共同对全世界宣布也可以是一个国际合作的典范 。

文章图片
同时 , 随着科学技术进步 , 如GPS技术、雷达测深技术、大地水准面精化、绝对重力测量技术、气象探测技术、登山装备技术及地学理论方法的完善 , 也为更加精确的测量珠峰高程创造了必要的条件 。

文章图片
党亚民表示 , 珠峰高程精确测量在地学研究中具有重要的理论价值 。 我们可以根据珠峰及邻近地区地壳水平和垂直运动速率变化 , 揭示了印度洋板块与亚欧板块相互作用力存在着不均匀强弱的变化 , 而这种强弱变化是引起我国大陆周期性地震活动的源动力 。 这些研究成果将对我国今后地震预报和减灾、防灾具有重要的实际意义 。 特别是精确的峰顶雪深、气象和风速等数据 , 也将为世界冰川监测、生态环境保护等方面的研究提供第一手资料 。

文章图片
【数据|高了一点点!给珠峰量身高有多难?测绘专家讲给你听】中尼珠峰测量联合技术委员会主席 自然资源部中国测绘科学研究院研究员 党亚民:那么这些数据对于珠峰这个地区乃至整个的喜马拉雅山脉 , 还有冰川气候的变化研究 , 都是提供了非常好的一个数据支撑 。 (珠峰高程数据)对全球的气候变化是一个非常好的很重要的指标 。 那么从这个层面讲的话 , 珠峰的高度对于我们全球变化的研究等相关的地球科学都是一个非常好的基础数据的支撑 。
来源:央视新闻
推荐阅读
- 浦峰|冬奥纪实8k超高清试验频道开播,冬奥结束后转入常态化运转
- 区块|面向2030:影响数据存储产业的十大应用(下):新兴应用
- 年轻人|人生缺少的不是运气,而是少了这些高质量订阅号
- 生活|气笑了,这APP的年度报告是在嘲讽我吧
- 人物|马斯克承认输给了巴菲特:曾尝试挑战喜诗糖果,但最终放弃
- 样儿|从太空看地球新年灯光秀啥样儿?快看!绝美风云卫星图来了
- 精度|将建模速率提升10倍,消费级3D扫描仪Magic Swift在2021高交会大显“身手”
- Tesla|最高涨幅21088元:特斯拉Model 3/Y入门车型价格调整
- 新机|快准稳,捕捉每个高光瞬间! 刘衡分享EOS R5拍摄体验
- 选型|数据架构选型必读:2021上半年数据库产品技术解析








