永动机|永动机与热力学定律_热力学|热力学第二定律|物理定

撰文 | 张伟伟
热力学三大定律分别为能量守恒、熵增定律和绝对零度无法到达，人们对热力学定律的认识也是纠正永动机思想的过程，是人类“美好思想”不断“碰壁”的过程，这些“碰壁”对于个人成长有着深刻的启示意义。
永动机的想法最初起源于印度，大约公元1200年前后，经由伊斯兰教世界传到了西方。欧洲最早的永动机方案是由法国亨内考（Villardde Honnecourt ， 13世纪人，留存有他的素描本，共有250幅素描）提供的。
亨内考想象有许多小球连接在一个有限位装置的轮子上，当小球在右侧时小球远离轮心，产生较大的力矩；而当小球到达左侧时，连接杆靠近轮缘，产生小的力矩。亨内考以此希望这个轮子可以在不输入额外动力的情况下，永不停歇的运动。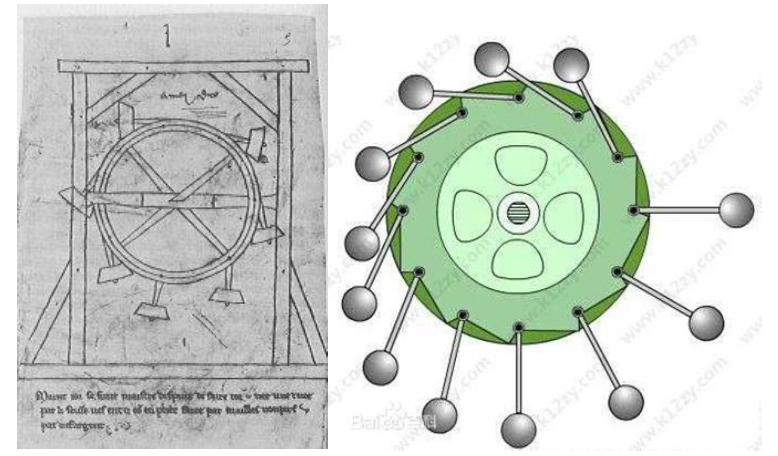

图1 亨内考永动机 (a)素描（约1203年） (b)复原图
这当然是不可能的，因为小球在右侧时力矩较大，但小球的分布是稀疏的，在左侧时，虽然小球产生的力矩小，但比较密集，因此，总有使轮子达到平衡的状态，这也意味着这个轮子并不会永久的运动下去。
文艺复兴时期，著名的意大利艺术家达芬奇（Leonardo da Vinci ， 1452-1519）也曾设计过一款永动机，如图2所示。该永动机将轮子的辐条做成小球滚动的轨道，并通过曲线设计让小球在其中滚动，如图2b所示，轮子左侧的小球远离轮心，产生大的力矩，右侧的小球靠近轮心，产生小的力矩。本质上达芬奇利用与亨内考相同的原理，不过达芬奇经过试验后发现，轮子初始运动不久后就会停在某个地方，根本不可能实现永动。因此他在设计图的旁边写下了一段文字：
"for everyaction there is an opposite and equal reaction"
对于任何运动，总存在反向、等大的反力。
这句话隐含的表达了永动机的不可能。牛顿第三定律表述为：相互作用的两个物体之间的作用力和反作用力总是大小相等，方向相反，作用在同一条直线上。达芬奇的标注，似乎表明达芬奇在牛顿前近2个世纪已经意识到了牛顿第三定律。

图2 达芬奇永动机 (a)素描（约1203年） (b)复原
尽管达芬奇很早否定了永动机的想法，但人们对永动机的尝试一直没有停止过，甚至到现在还有各种各样的永动机设计方案。
这类永动机代表了一种“不劳而获”的想法，随着热力学第一定律的发现，这类永动机就被否决了。这期间，德国医生迈尔（Julius Robert von Mayer,1814-1878），英国物理学家焦耳（James Prescott Joule,1818-1889），德国物理学家（Hermannvon Helmholtz ， 1821-1894）做出了关键性的贡献。

图3 热力学第一定律创立者
迈尔是一位德国医生， 1840年，他作为随船医生到达印度尼西亚，有些船员因水土不服而生病。在德国常采用放血疗法医治水土不服，而放出的血通常为黑红色，迈尔却发现此时船员的血依然是鲜红色的。从这一现象，迈尔想到了血液红是由于富含氧，而氧在体内维持燃烧产生热。在印度尼西亚，由于气温高，人不需要太多的热量，因此氧就被保留下来致使血液鲜红。迈尔顺着这条思路，一下打开了一扇他从未意识过的大门。迈尔想到肉和菜是身体热量的物质基础，那肉和菜的热量如何而来，迈尔又想到了光合作用。迈尔越想越多，从太阳能想到植物能、动物能、到人的食物、氧化反应、人体热量等等，最后归结为一点：能量发生了转化。
迈尔返回欧洲后，不久撰写了On the Quantitative and Qualitative Determination of Forces（1841年）（百度百科中译为：论无机界的力，在德国力force有能量的意思），在该论文中迈尔提出了能量“无不生有，有不变无”、“原因等于结果”等重要思想，并用自己的方法测定了热功当量为365 (千克.米/千卡)。要知道，在此之前，人们对于热和燃烧等现象，还一直停留在热质说，能量转换、守恒等思想很难被人们接收。迈尔将他的研究成果提交到《物理年鉴》（Annalen der Physik），但很快就被拒稿，并被人们嘲笑为疯子。
与迈尔同时期的英国物理学家焦耳在这时也注意到了能量转换， 1843年，焦耳设计了巧妙的实验较为精确的测定出了热功当量为428.9 (千克.米/千卡) ，此后又分别于1845、1850年更加精确的测定了热功当量，焦耳的风头彻底盖过了迈尔。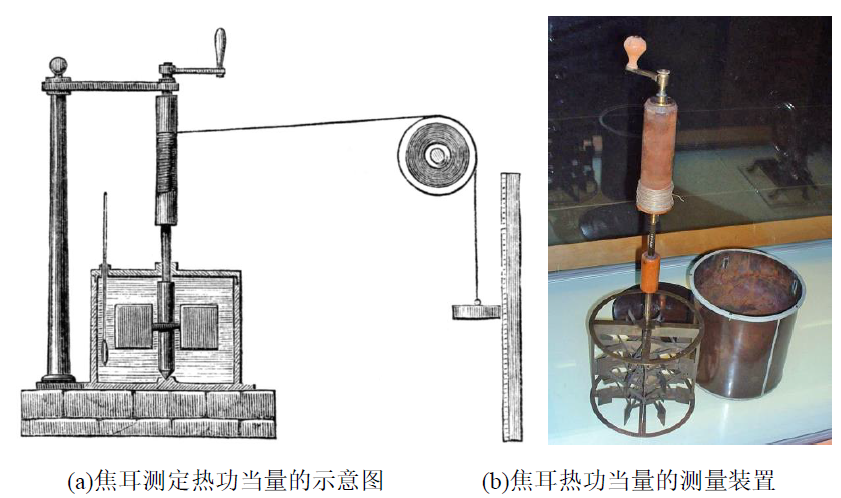

图4 焦耳热功当量的测量
1847年，德国的另一位物理学家亥姆霍兹（早年从事医学、生物学的研究）发表了On theConservation of Force《论力的守恒》，在该文中主要提出了三个观点：1. 一切科学都可以归结为力学；2. 强调了力所传递的能量或它所作的功来量度力；3. 能量是守恒的。亥姆霍兹首次用数学化形式表述了在孤立系统中机械能的守恒，把能量的概念推广到热学、电磁学、天文学和生理学领域，提出能量的各种形式相互转化和守恒的思想，这就是热力学第一定律。根据这一定律，亥姆霍兹明确的提出由于能量具有守恒性，不能凭空产生，因此永动机的想法不可能实现。
人们将违反热力学第一定律的永动机称为第一类永动机，以此来区别于后来那些不违反热力学第一定律的其它永动机方案。如第二类永动机，人们承认能量守恒，只是希望永动机的能由海洋、大气乃至宇宙提供，在这些取之不尽的能源下实现永久运动。第二类永动机的想法最终被热力学第二定律所否决。
在热力学第一定律提出的时期，也是蒸汽机蓬勃发展的时期。然而人们对蒸汽机效率低下的问题却一筹莫展。最初的纽卡门机按照燃料热值计算，其效率只有0.5% ，也就是说燃烧1000吨的煤，只有相当于5吨的煤做了功，其余的995吨都白白浪费掉了。即便到了1840年，制造精良的冷凝式蒸汽机，其效率只有8%左右，这实在令人难以接受。这或许也是人们向往第二类永动机的原因所在。
历史上第二类永动机的案例很少， 19世纪70-80年代英国兽医和发明家加吉（John Gamgee ， 1831-1894）设计出了第二类永动机的原型机，并成功说服了美国海军总工程师和加菲尔德（Garfield）总统支持他的设计。加吉的设想是这样：给轮船装上一个大容量的液氨容器，然后利用周围空气的热量使氨气化，氨在膨胀后推动活塞做功，再让氨气通过与海水接触的冷管道进行冷却，使氨气变为液态的氨。整个循环不需要任何外部的燃料，仅依靠大气和海水的热源。
这个诱人的想法，从50年前卡诺的研究中就会被轻易的否定。 1824年，法国被誉为“热力学之父”的卡诺（Nicolas Léonard Sadi Carnot ， 1796-1832）发表了《关于火的动力》，提出了卡诺定理，他指出理想热机的热效率为
η=1-T2/T1 (1)
其中， η为热机效率， T2表示低温热源， T1表示高温热源（绝对温度）。这表明热机效率依赖于低温和高温两个热源，温差是热机热效率输出的前提。对于加吉所设计的第二类永动机，液态氨变为气体后，由于氨气冷凝所需要的温度为-33oC ，仅通过海水是无法使其再变为液氨的。也就是说加吉所谓的永动机，只能做一个冲程的运动，而无法产生循环往复，随着液氨的逐步气化，加吉永动机必将最终走向停止。
卡诺去世46年后（1878年），他的论文被克拉贝隆（Benoit Pierre Emile Clapeyron, 1799-1864），开尔文（LordKelvin, 1824-1888），克劳修斯（Rudolf Julius Emanuel Clausius ， 1822－1888）等人重新关注。其中，克拉贝隆建立了理想气体的状态方程，
PV=nRT (2)
其中， P表示气体压强， V表示体积， n表示摩尔数， R为摩尔气体常数， T为绝对温度。还依据示功图描述了卡诺循环，这为热力学分析奠定了重要基础。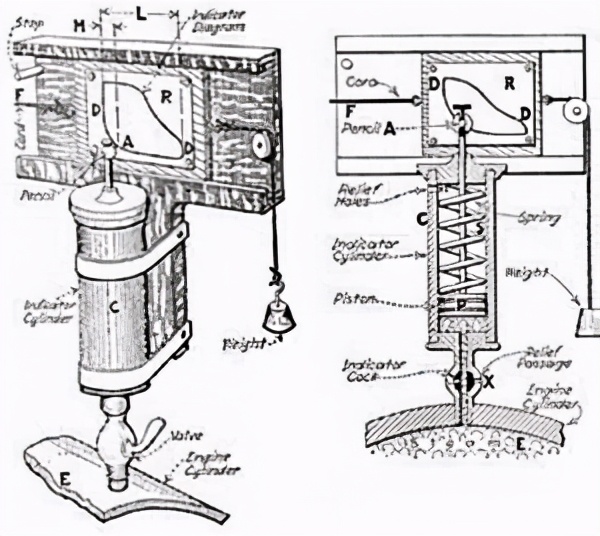

图5 瓦特示功器。 1800年瓦特发明了蒸汽示功器，其中的曲线即为气体的P-V曲线，为克拉贝隆的研究提供了基础（1834）
1850年，克拉贝隆的研究引起了克劳修斯的关注，克劳修斯指出卡诺定律如果成立必须满足第二热力学定律，即“不可能把热量从低温物体传向高温物体而不引起其它变化。 ”克劳修斯还引进了“熵”的概念。笼统的讲，熵表征了热力学系统分子运动的混乱程度：系统温度越高，分子运动越混乱，熵值越高；相反，系统温度低，分子相对有序的运动，熵值越低。由于热只能从高温物体传向低温物体，而不能从低温物体自发的传向高温物体，因此系统在自发状态下总是沿着温度升高的方向发展，热力学第二定律也被称为熵增定律。
1851年，爱尔兰物理学家开尔文也独立的给出了第二定律的另一种描述：不可能制成一种循环动作的热机，从单一热源取热，使之完全变为功而不引起其它变化。因为按照卡诺定理，功可以完全变成热，而热却不能完全的产生功（热机效率不可能达到1），总会伴随着热从高温热源向低温热源耗散损失。第二类永动机通常描述为“旨在从单一热源吸热使之完全变为有用功而不产生其它影响的热机” ，显然与热力学第二定律相矛盾。
热力学第一、第二定律的诞生彻底终结了第一、第二类永动机，但人们对美好生活的追求绝不会停止，人们又指望设计一种完全没有无用损伤，热效率可达100%的永动机，这被称为第三类永动机。
从卡诺热机效率的式(1)可以看出，当低温热源T2等于绝对零度（-273oC）时，热机效率可以达到100% 。但是T2=0是不可能的，根据状态方程(2)可知，当T等于0时，要么P=0 ，要么V=0 ，而实际上气体总会有一定的体积和压强，绝对零度是根据状态方程的外推结果，并不是一种真实情况。而绝对零度不可能达到被称为热力学第三定律，是第三类永动机的终结者。
相比于第一、第二定律，第三定律的提出要晚很多，大概在1906-1912之间由德国化学家恩斯特（Walther Nernst ， 1864-1941）提出。恩斯特在1912年的一篇论文中写道：“任何程序都不可能在有限的步骤中使等温线T=0” ，即绝对零度不可能达到。后来，普朗克（Max Planck ， 1858-1947）给出了热力学第三定律的另一种表述：所有纯晶体均质材料在内部平衡状态下，其熵在绝对零度时都为0（在普通的热力学中只关心熵的变化，并不关心熵的取值）。
简单来看，第三定律可以从卡诺定律导出，似乎意义不大，其实不然。恩斯特定律的提出为化学家根据热量测量确定化学反应的自由能提供了依据。此外，恩斯特在实验中发现，在低温条件下，比热显着下降，并大胆的预测了比热可能会在绝对为零时消失，这对量子力学的发展提供了强有力的驱动力。
第三类永动机人们没有从机械的角度来考虑（太难了），通常认为理想单摆在不受阻力作用时，就是第三类永动机。此外，也有人将“太阳-行星”体系、“原子-电子”体系视为第三类永动机，或许它们没有与环境的能量交换，不过这也不一定就是真理。
1990年代，美国人在亚利桑那州的沙漠里曾进行过一个称为“生物圈2号”（Biosphere 2 ，美国人将地球本身命名为1号）的实验，该项目占地1.27公顷，以地球北回归线和南回归线间的生态系统为样板，设计有热带雨林、热带草原、海洋、沼泽、沙漠等5个野生生物群落和集约农业区和居住区2个人工生物群落。生物圈2号，被构造成一个全封闭系统，为了避免内部压力变化破坏玻璃窗板，生物圈2号设计两个薄膜覆盖的空间，它们可随压力改变体积，被称为生物圈2号的“肺” 。

图6 生物圈2号
生物圈2号共在1991至1993年进行了两期实验，遗憾的是，研究人员发现生物圈2号的氧气与二氧化碳的大气组成比例，无法自行达到平衡；水泥建筑物也会影响到正常的碳循环；此外，物种多样性相对单一，缺少足够分解者作用，多数动植物无法正常生长或生殖，其灭绝的速度比预期的还要快。经广泛讨论，确认“生物圈2号”实验失败。
生物圈2号希望构建一个可永远运动的封闭系统（该系统也被视为在太空构建封闭生物圈的先驱），该系统可自行循环，是一个转化效率可达100%的“热系统” ，或许生物圈2号就是违背了热力学第三定律，最终导致了它的失败。
回顾三类永动机的破灭和热力学三大定律，或许可以得出一些个人成长的启示：在生活中只有付出才能得到回报，因为根据能量守恒，任何不劳而获的想法都是徒劳的；
热力学第二定律告诉我们自然系统的演化具有方向性，无论我们做什么，都会产生永久性的影响。在我们做出某些决定时，一定要加倍小心，因为一旦我们做了相应的事情，就无法回到原状，这大概就是我们常说的“世界上没有后悔药” 。这也深刻的启示我们，如果所做的事是符合社会价值观、对社会和民族有益的事情，它的益处迟早会表现出来，而做相反的事，它的坏处也迟早会影响到我们的生活；
热力学第三定律告诉我们不要指望自己的付出会100%的得到回报，事事不尽如人意就是客观规律，要学会与遗憾和平共处。大自然是如此的吝啬，不过不要气馁，正如生物圈2号，是大自然逼迫人们在相对封闭空间内留出一扇通往外界的大门！
参考文献
热力学第三定律.
https://en.wikipedia.org/wiki/Third_law_of_thermodynamics
第二类永动机.
https://eandt.theiet.org/content/articles/2017/03/eccentric-engineer-the-perpetual-motion-machine-that-fooled-a-president/
白静. 由迈尔的科学蒙难谈热力学第一定律教学中的潜科学分析[J]. 中国科教创新导刊, 2008, 000(017):136-136.
永动机的历史
https://www.lockhaven.edu/~dsimanek/museum/people/people.htm
【永动机|永动机与热力学定律】本文经授权转载自微信公众号“力学酒吧” 。

永动机|永动机与热力学定律

推荐阅读

关于勇敢坚强的QQ个性签名很励志只有你劝我别逞强

?水瓶座是个很差的星座吗水瓶座是个残忍的星座

水煮蛋烧什么好吃水煮蛋烧什么好吃又简单

口袋妖怪红宝石攻略神兽抓法

仓颉造字的传说

宫颈口有一个小颗粒是怎么回事尖锐湿疣的症状是什么

写一句做人道理的名言

下一届奥运会会不会有滑板项目

有关心酸伤感的句子

常喝胡萝卜汁的好处有哪些

柯桥金色华庭是安置小区吗

干姜与吴茱萸的功效比较有何不同与相同作用

连衣裙怎么搭减龄什么颜色的连衣裙好看

计算机信息安全的目标是什么

弹一闪怎么使用弹一闪是什么意思

新玛特会员卡等级

石韦叶的性味归经与作用功效禁忌

海南省的行政中心是

我的世界kill指令怎么杀别人我的世界kill指令如何使用

霍政谚演过的电视剧霍政谚主演了哪些电视剧