Mahjong|按照概率学原理，你这牌一看就胡不了_研究|花色|对子|李志光|组合

撰文比邻星
春节假期，独乐乐不如众乐乐。
如果要选择一种声音代表新春佳节的团聚，除了噼里啪啦的鞭炮、杯盏相碰的清脆，一句“三缺一”和麻将桌上哗啦啦的搓麻声必定占有一席之地。
麻将在不同段位的玩家眼中代表着不同维度的世界。入门级小白只专注于面前的牌，久经沙场的老手更有大局观，心中装着整个牌桌的乾坤。而在一名理科生眼中，麻将是一场概率游戏和策略博弈。

文章图片

19世纪的麻将牌长这样 | 图源：Wiki
不过话说回来，还真有数学家发表了关于“麻将数学”的研究论文，不仅编写程序计算胡牌的概率，更是致力于开发AI打麻将的技能。当然，机器人怎么打麻将倒是后话了，对于各位玩家而言，这些研究最大的价值在于能给麻将桌上的牌局以“专业”的理论指导。
故事还要从清一色讲起。
先补充点背景知识。标准麻将牌包含“筒”、“条”、“万”、“风”和“箭”五套花色，每种牌有4张是相同的。 4名玩家初始摸得13张牌，之后按照逆时针摸一张牌再打出一张牌，直到他摸到最后一张牌， 14张牌可以凑成23333的排列组合，即为胡牌。

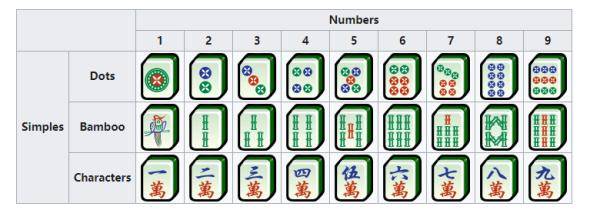
文章图片

从上到下分别为“筒”、“条”、“万” | 图源：Wiki
用公式表示就是
m*AAA+n*ABC+DD m ， n可以为0
如果最终胡牌的牌面为同一花色，就叫清一色。
一个叫李志光的数学家发现了一种有趣的牌形。

文章图片

【Mahjong|按照概率学原理，你这牌一看就胡不了】好牌
图源：Mathematical aspects of the combinatorial game “Mahjong”
仔细看，你会发现下一张只要摸到的也是筒，不管是一筒到九筒中的哪一张，都可以胡牌。这牌，只要一推倒，众人定有不明觉厉之感。
这样的牌形叫“九门”（Nine Gate）, 李志光随后联想到，类似的“八门”、“七门”、“六门”……都有什么样的牌形，哪种出现的概率更高？
至此开始，一个娱乐问题成功上升为科研课题，行话叫“k门问题” 。
用数学符号代表刚才的牌形，那就是
X1X1X1X2X3X4X5X6X7X8X9X9
计算概率，大体的思路就是尝试所有Xi的组合，然后检验每种组合是否符合k门的要求。这样的重复性运算，交给Python程序就够了。

文章图片

一段源代码截图网址链接：
https://cklixx.people.wm.edu/mathlib/Mahjong.py
结果是这样的。 “九门”的组合有且仅有一种，它出现的概率为0.000113；八门有16种；一门的组合则有14067种，出现的概率是0.148 。
k门问题只是个开始，发现能用数学方法研究麻将，另一个团队也跃跃欲试。他们关注到的问题是——如何判断距离胡牌还差几张牌？研究结果整理为论文《来玩麻将啊！》（Let’s play Mahjong!）

文章图片

都是科研论文，这篇的画风就很可爱
这个问题很实用了，理解了其中奥义，你也能拥有牌局的大局观。来看看他们是怎么算的。
首先需要用数学语言定义每一种牌形。他们选择了一对数字（c, n）， c表示花色， 0为条、1为万， 2为筒；n表示具体的数字。比如（0, 3）就是三条，（1, 5）就是五万。

文章图片

（2,7）和（2,5）| 图源：flicker
接下来设置一段数列V ，即14个（c, n）的集合，用来表示完整的牌面。这时你就可以用逻辑语言定义出胡牌（complete）的条件。
最后一步是设计一个变量，定量地表示牌面的好坏。研究者引入了“缺牌数”的定义，也就是距离运算到胡牌状态，还差几张牌。
接下来的运算结果请收好，这是一份科学的打牌秘籍。
基础版——清一色
如果你已经凑出了两个“3连”（包括刻子和顺子），且它们不连续，那么缺牌数小于等于2；
如果你的牌面是以下两种情况之一，那么缺牌数为3
5个对子+一个杠；
5个对子+1个刻子+1张单牌
进阶版——多花色
对于任意组合的一副牌，最大缺牌数为6 。要置换6张牌才能胡的牌面就是最烂的牌；
如果你的牌面是以下3种情况之一，那么缺牌数小于等于5
两个不连续的“3连”（包括刻子和顺子）；
一个“3连”和一个“准3连”（只需要碰一下或者吃一个就能凑出刻子或顺子）；
4个“准3连”
面对具体的牌面时，置换麻将牌的方案不止一种，此时需综合考虑缺牌数和胡牌成本，以及方案的可行性。
举个栗子,如果你的牌面是这样的，那么你可以考虑3种搭配方案

文章图片

先把牌码上，看起来顺眼一些。

文章图片

第一种方案里， “准3连”B1B3还差一张B2（二条），但是整副牌中已经没有多余的二条，因此这种方案无效。方案二和方案三都是可行的，但是方案三的缺牌数更小，所以更优。
作为中国的经典传统游戏，麻将的玩家覆盖率在整个游戏江湖遥遥领先。不同地区有不同的打法。几分技巧、几分运气，还有好几分的乐趣。这种独特的牌类游戏也慢慢漂洋过海，传入了包括欧美国家在内的世界许多地方。还有研究证实，麻将的益智作用有益于阿尔茨海默病患者。

文章图片

美国的娃们在课外活动课上学习打麻将 | 图源：Wiki
当然，专业的科学家费劲编写程序来还原麻将的游戏规则，初衷倒不是为各位玩家搞一套打牌指南，而是为了开发人工智能。毕竟围棋高手阿尔法狗和阿尔法零相继横空出世，麻将高手机器人也指日可待。

文章图片

问：图中有几个人在打麻将？| 图源：unsplash
各位麻将高手，你期待和机器人PK的那天吗？
无标注图片来源网络。
参考资料:
1.Yuan Cheng, Chi-Kwong Li, and Sharon H. Li. Mathematical aspect of the combinatorial game “Mahjong”. ArXiv:1707.07345, 2017.
2.Sanjiang Li , Xueqing Yan. Let’s Play Mahjong! arXiv:1903.03294v1
来源：把科学带回家
编辑：Eric
[责任编辑: ]

Mahjong|按照概率学原理，你这牌一看就胡不了

推荐阅读

苹果红的一面是哪个方向

孜然风味烤羊排的做法（老年菜谱）

哪些食物不能用微波炉加热哪些食物不可以放在微波炉加热

玫瑰花需要每天浇水吗，浇水可以用自来水吗

内裤l码是多大尺寸

鲜菇怎么做好吃鲜菇的家常做法

库存周转率是什么意思

中秋节祝福语微信给爸妈的中秋节祝福语给爸妈的中秋节祝福语微信

投石车原理与设计

红烧鱼块的做法（老年菜谱）

吃什么能够保护眼睛？

吃辣条肚子疼怎么办

iPhone8Plus处理器介绍苹果8p是什么处理器几核的

甘肃十大名菜拔丝洋芋上榜河西羊羔肉是特色

二婚结婚证和一婚结婚证的区别

中国哪些地方景色很美

脍炙人口的脍炙什么意思

训练八哥犬的注意事项有哪些

恐龙是怎样消失的

儿童提高免疫力的方法有哪些