碰撞|深度学习如何学习直观物理学_速度|研究|问题|直觉|推理|物体

机器之心分析师网络
作者：仵冀颖
编辑：Joni

从直观物理学讲起。

在这篇文章中我们讨论的是一个对于非物理学专业的人来说相对陌生的概念 --- 直观物理学（Intuitive Physics），我们聚焦的是深度学习是如何学习直观物理学的。
首先，我们从究竟什么是直观物理学谈起。人类能够了解自己所处的物理环境，并与环境中动态变化的物体和物质相互作用，对观察到的事件发展趋势做出近似性的预测（例如，预测投掷的球的轨迹、砍掉的树枝将坠落的方向）。描述这些活动背后规律的知识就是直觉物理学。直觉物理学几十年来一直是认知科学领域一个活跃的研究领域。近年来，随着人工智能相关新理论方法的应用，直觉物理学研究重新焕发了活力。研究人员利用直觉物理学的模型模拟行为研究的结果，而这些行为研究将心理物理测量应用于复杂动态显示的感知和推理。
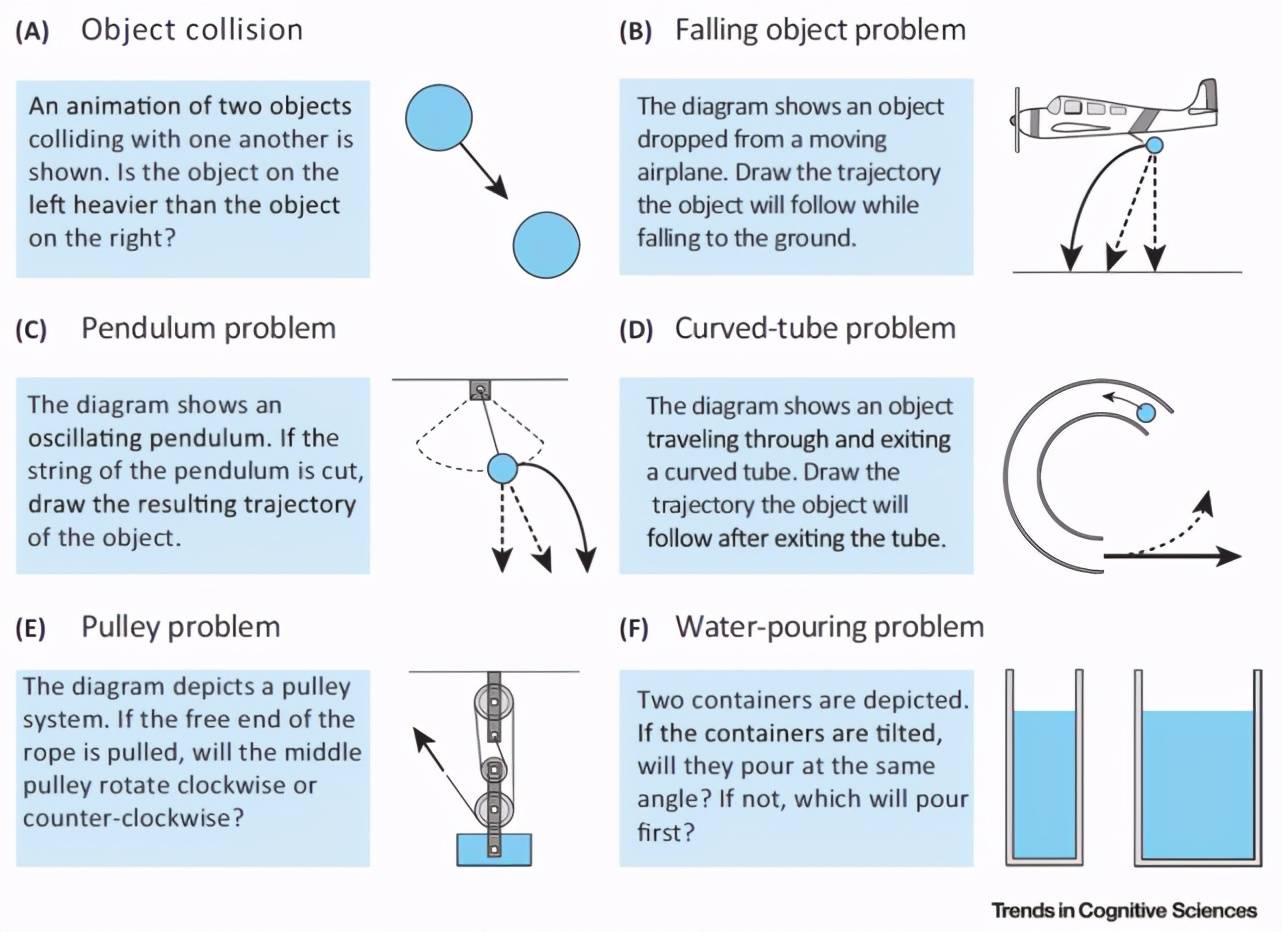
图 1 给出了几个常见的直觉物理学问题示例 [1] 。图 1 中的任务是对各种情况下物体和物质的属性或运动进行推理。除了物体碰撞判断（A），通常通过物理系统的静态图来描述问题。在（B–D）中，不间断线表征正确的轨迹，而间断线表征常见的错误预测。概率模拟框架（Probabilistic simulation framework）成功地预测了人们对动态显示中物体的属性（A）和运动（C）的期望，以及两个充液容器的浇注角度（F）。不过，人们在进行推理判断时一般是根据不同的情况、不同的运动理论进行推理的。这导致人类感知和推理物理情况的能力普遍不高，尤其是在抛射物运动和物体碰撞的情况下。

文章图片

图 1. 直觉物理学问题示例
在这一章中，我们介绍几种直观物理学的研究方法，启发式方法、概率模拟模型和深度学习方法。如图 2 所示。

文章图片

图 2. 确定两个碰撞物体相对质量的三种计算方法的描述。模型之间的主要区别在于学习的作用（启发式方法最小，概率模拟有限，深度学习比较大）。（A）在启发式模型中，假设观测到的速度与环境中的物理速度相等（即直接感知速度）。比较碰撞后的速度，并假设碰撞后以最大速度移动的物体较轻。启发式模型中没有考虑学习的作用。（B）概率模拟模型将先验放在隐藏的物理变量上。运动先验将感知速度偏向慢运动。通过比较模拟的最终速度和观测的速度，确定不同质量比的可能性。学习可能会影响推理所涉及的先验知识。（C）在一个深度学习模型中，卷积神经网络（CNN）被训练成二维图像的输入和输出对象属性（质量和摩擦力）。然后使用 CNN 从先前看不见的图像数据中预测对象属性。这种方法使用了自下而上的学习过程。
除了涉及单个物体运动的研究外，早期关于两个物体碰撞的研究还表明，根据牛顿原理，人类的判断常常会偏离预期。例如，考虑一个初始运动物体（运动物体）与一个初始静止物体（抛射物体）碰撞的情况。当运动物体对抛射物体的物理效应相对较小时（例如，抛射物体的碰撞后速度小于运动物体的碰撞前速度），人们做出的因果关系判断会比物理效应大时更强烈（例如抛射物体的碰撞后速度大于机动物体的碰撞前速度）。这一发现被称为启发式方法（Heuristics ），也就是最经典的直观物理学方法：人们可以根据显著的知觉线索使用下面两个规则来推断碰撞物体的属性。（i）碰撞事件后移动较快的物体较轻（速度启发式；如图 2A 所示），（ii）以较大角度偏转的物体较轻（角度启发式）。然而，尽管这些启发式方法在某些情况下解释了人类对碰撞物体相对质量（Relative Mass）的判断，但它们并不能推广到其他情况。
启发式方法其中一个难点，是显性物理概念是如何从经验中衍生出来的？以及它们与隐性物理知识的相互作用程度如何？这两个核心问题还没有确定答案。造成这种不确定性的一个原因似乎出自系统概念分类的困难，而这种困难源于物理环境中的知觉模糊性表述，或者任务中所涉及到的知觉以及任务中物理变量的无效表示。例如，当物体从摇锤中释放后绘制其轨迹时，最直接的想法是“垂直向下运动（straight-down）” ，因为物体在所示（静态）位置的速度是模糊的。或者，人们会认为从运动物体上落下的物体会垂直向下运动，因为这种运动方式代表了物体相对于运动物体的感知运动。此外，这种问题在旋转容器上绘制水位（即水位问题）时也会出现，即使已经明确指出了液体表面应保持水平而无需考虑容器的方向。此时，造成判断偏差的原因是无效表示：使用轴平行于容器表面的以对象为中心的参照系。在这种不确定性下，人们对物理量的判断（例如，两个物体相互碰撞产生的力）与牛顿原理不一致。因此，直觉物理学方法应当能够考虑到（i）认知结构和物理结构之间的对应关系，（ii）不同问题背景下认知表征的性质，（iii）物理近似在复杂显示中的作用，（iv）预测判断任务中显性概念与隐性理解的交互作用。
近年来，基于贝叶斯推理（Bayesian inference）的新的理论方法，特别是噪声牛顿框架（Noisy Newton Framework），使直觉物理学的研究重新焕发了活力，它将真实物理原理与感官信息的不确定性相结合。基于噪声牛顿框架的模型假设，人们将带噪声的感官输入与物理情境下的感知变量，以及物理变量的先验信念（Prior Belief）相结合，并根据牛顿物理学对这些变量之间的约束进行建模。例如，在碰撞事件（Collision Event）中，通过模拟数千种物理情况来建模预测过程。在每个模拟过程中，使用牛顿定律对感知和物理特性的采样变量进行计算而得到物理结果。尽管大多数感知变量都是可观察的（例如速度、位置），但仍然有必要将客观证据（观察）转化为主观估计，方法是将噪声感官输入与感知线索统计规律的先验值相结合。另外，一些物理性质（如质量、粘度）是不能直接观察得到的，必须从感官观察和 / 或物理世界的一般知识中推断出来，如图 2B 所示。
噪声牛顿框架有效地调和了人类判断和牛顿物理学之间的一些矛盾。在噪声牛顿框架下，通过将噪声信息传递给物理引擎来实现推理，物理引擎由物体碰撞时的动量守恒原理定义。在假设感知输入到物理期望的转换符合牛顿原理约束的前提下，有关对象动力学（Object dynamics ）的知识被 “写入” 模型。概率模拟模型（Probabilistic Simulation Model）的核心思想是人类构造关于物理情境的概率心理模型，通过心理模拟来推断未来的物体状态。心理模拟的作用得到了机械推理的支持，它证明了人们通过构造和转换空间表征来回答关于物体和物质行为的问题，从而对物理系统进行推理。空间表征意味着物体在物理世界中的位置、运动和隐藏属性以及它们之间的相互作用在大脑中可以进行概率学的编码和表征。
最近的神经科学研究结果表明，心理模拟过程可以以概率论来描述，这些区域与大脑的 “多需求” 系统重叠。概率模拟模型通过将噪声信息处理与先进的基于物理的图形引擎相结合来模拟未来的对象状态，从而在物理推理任务中做出判断。在每个模拟中，场景中感知变量和物理变量的值根据模拟对象位置、速度和属性的噪声信息处理的分布进行采样。基于感知和物理输入的采样状态，使用近似牛顿原理的 “直观物理引擎（Intuitive Physics Engine）” 来模拟未来的对象状态。然后查询每个模拟的结果以形成预测判断，例如，是否有一个积木塔倒塌或有多少液体落入指定区域。最后，在模拟中聚合判断以形成预测的响应分布。选择仿真模型中的参数，使分布能够准确反映人的行为。概率模拟模型建立在两个基本组件上：作为物理引擎输入的物理变量和引擎中编码的物理原理。一些物理变量（如速度和物体位置）可以直接感知，尽管感知值可能会被神经噪声和一般先验（如运动感知中的缓慢平滑先验）所扭曲。还有一些物理变量（如质量、粘度、密度和重力）是无法直接感知的，那么问题是，人类如何从视觉系统中的低级特征中推断出这些物理属性的？
深度学习模型的最新进展表明，一种潜在的计算机制可以从视觉输入中推断物理属性，并对物理情况做出预测。这种方法出现在机器学习领域，是基卷积神经网络（CNNs）实现的。卷积神经网络以像素级编码的图像作为输入，通过分层处理信息，学习从简单的视觉成分（如边缘）到更复杂的模式和对象类别的多层次抽象表示。具体的，一种混合方法（Hybrid approach）将基于知识的物理模型与基于学习的识别网络相结合，用于从视觉输入中预测物理属性。这种混合方法在解释人类直观的物理预测能力方面取得了一些成功。如图 2.C 中，利用深度学习网络，通过多个处理层将动态视觉输入（二维图像序列）映射到两个碰撞物体的推断属性（质量和摩擦力）。这一过程有效地逆转了生成物理过程的一个关键组成部分。 CNNs 基于与对象属性相关的图像数据进行训练，对象属性是通过将视觉输入的关键特征与物理引擎的模拟输出相匹配来确定的。 CNNs 具有与人类相当的推断能力，表明基于学习的方法可以有效地与基于知识的物理引擎集成，以推断环境中物体的属性和动力学。
由上面对直观物理学的回顾可以看出，以概率模拟为基础的物理推理方法一般都假定真实的物理原理是作为先验知识提供的。从计算的角度来看，基于样本（Exemplar）的方法可以将物理情况的观察实例表示为与相应属性相关联的 N 维空间中的向量。新观察到的实例的期望属性是通过对属于每个可能分类的实例的相似性度量求和来预测的。然而，尽管基于样本方法通过模仿物理知识在受限的物理区域内做出了合理的预测，但它不能推广到先前未知的区域中。基于深度学习的模型则具有 “学习” 的能力，可以从先前未知的数据中预测到物体的属性。本文重点关注的就是深度学习如何更好的学习直观物理学。具体的，文献 [2] 中提出的模型可以从一个单一的图像映射到一个牛顿假设（Newtonian scenario）状态。这种映射需要学习微小视觉和上下文线索，以便能够对正确的牛顿假设、状态、视点等进行推理。然后可以通过借用与牛顿假设建立的对应关系的信息，对图像中对象的动力学进行物理预测，从而根据静止图像中查询对象的速度和力方向来预测运动及其原因。文献 [3] 关注直接从视觉输入预测物理稳定性的机制。作者没有选择显式的三维表示和物理模拟，而是从数据中学习视觉稳定性预测模型。文献 [4] 关注了一个真实世界的机器人操作任务：通过戳来将物体移动到目标位置。作者提出了一种基于深度神经网络的新型方法，通过联合估计动态的正向模型和逆向模型，直接从图像中对机器人的交互动态进行建模。逆向模型的目标是提供监督，以构建信息丰富的视觉特征，然后正向模型可以预测这些特征，并反过来为逆向模型规范化特征空间。文献[5] 设计并实现了一个利用视觉和触觉反馈对动态场景中物体的运动进行物理预测的系统。其中感知系统采用多模态变分自编码神经网络结构，将感知模式映射到一个共享嵌入，用于推断物理交互过程中物体的稳定静止形态。
1、深度学习处理不同直观物理学问题的研究进展
1.1 Newtonian Image Understanding: Unfolding the Dynamics of Objects in Static Images [2]
https://arxiv.org/abs/1511.04048
本文重点研究在静态图像中预测物体动态的问题。人类的感知系统具有强大的物理理解能力，甚至能够对单个图像进行动力学预测。例如，大多数人都能可靠地预测排球运动的动力学表现（Dynamics），如图 3 所示。

文章图片

图 3. 给定一个静态图像，目标是推断查询对象的动力学表现（作用在对象上的力以及对象对这些力的预期运动
1.1.1 基本思路
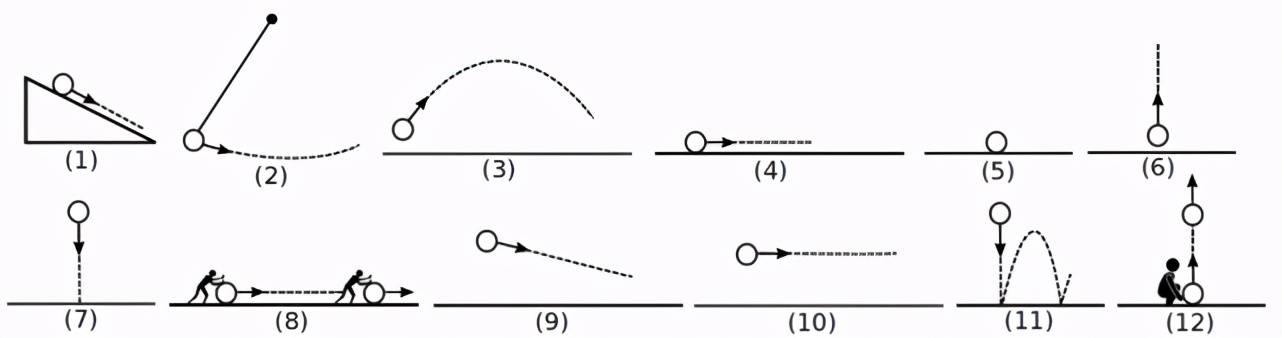
从图像中估计物理量化指标是一个极具挑战性的问题。例如，计算机视觉文献并没有提供一个可靠的解决方案来从图像直接估计质量、摩擦力、斜面角度等。因此，本文作者将物理理解问题描述为从图像到物理抽象的映射，而不是从图像直接估计物理量。作者遵循与经典力学的相同原理，并使用牛顿假设作为物理抽象，具体场景如图 4 所示。给定一个静态图像，作者的目标是对查询对象在三维空间中的长期运动进行推理。为此，作者使用一个称为牛顿假设（图 4）的中间物理抽象，由游戏引擎渲染。

文章图片

图 4. 牛顿假设是根据不同的物理量来定义的：运动方向，力等等。我们使用 12 个假设来描述。圆表示对象，箭头表示其运动方向
本文使用牛顿神经网络（Newtonian Neural Network ， N^ 3）学习牛顿假设中的一个从单一图像到状态的映射。牛顿假设的状态对应于游戏引擎生成的视频中的特定时刻，并包含该时刻的一组丰富物理量（力、速度、三维运动）。通过映射到牛顿假设的一个状态，作者可以借用对应的物理量化指标，并使用它们来预测单个图像中查询对象的长期运动趋势。
在牛顿假设中，从一幅图像到一种状态的映射需要解决两个问题：（a）找出哪个牛顿假设能够最好的解释图像的动力学；（b）在假设中找到与运动中物体状态相匹配的正确时刻。通过引入上下文和视觉线索，可以解决第一个问题。然而，第二个问题涉及到对微小视觉线索的推理，这种推理对于人类来说都是非常困难的。 N^ 3采用数据驱动的方法，利用视觉线索和抽象的运动知识同时学习（a）和（b）。 N^ 3利用二维卷积神经网络（CNN）对图像进行编码。为了了解运动， N^ 3使用 3D CNNs 来表示牛顿假设的游戏引擎视频。通过联合嵌入， N^ 3学习将视觉线索映射到牛顿假设中的精确状态。
1.1.2 N^ 3模型分析
作者首先构建了一个视觉牛顿动力学（VIsual Newtonian Dynamics ， VIND）数据集，其中包含游戏引擎视频、自然视频和牛顿假设对应的静态图像。使用游戏引擎构建牛顿假设。游戏引擎将场景配置作为输入（例如，地平面上方的球），并根据物理学中的运动定律及时模拟它。对于每一个牛顿假设，作者从不同的角度给出了相应的游戏引擎假设。总共获得 66 个游戏引擎视频。对于每个游戏引擎视频，除了存储 RGB 图像外，还存储其深度图、曲面法线和光流信息。游戏引擎视频中的每一帧总共有 10 个通道。此外，作者还构建了一组描述运动物体的自然视频和图像。目前用于动作或物体识别的数据集不适合于本文的任务，因为它们要么包含了一些超越经典动力学的复杂运动，要么就不显示任何运动。
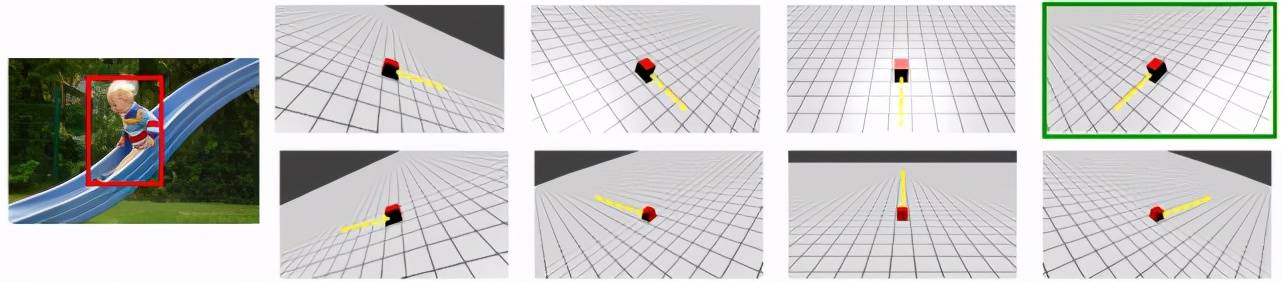
作者为每个图像 / 帧提供三种类型的注释：（1）至少一种牛顿假设描述的对象的边界框注释，（2）视点信息，即游戏引擎视频的哪个视点最能描述图像 / 视频中的运动方向，（3）状态注释。对应于牛顿场景（1）的示例游戏引擎视频如图 5 所示。

文章图片

图 5. 视点注释。要求注释者选择最能描述图像中对象视图的游戏引擎视频（在牛顿假设的 8 个不同视图中）。游戏引擎视频中的对象显示为红色，其移动方向显示为黄色。带有绿色边框的视频是选定的视点。
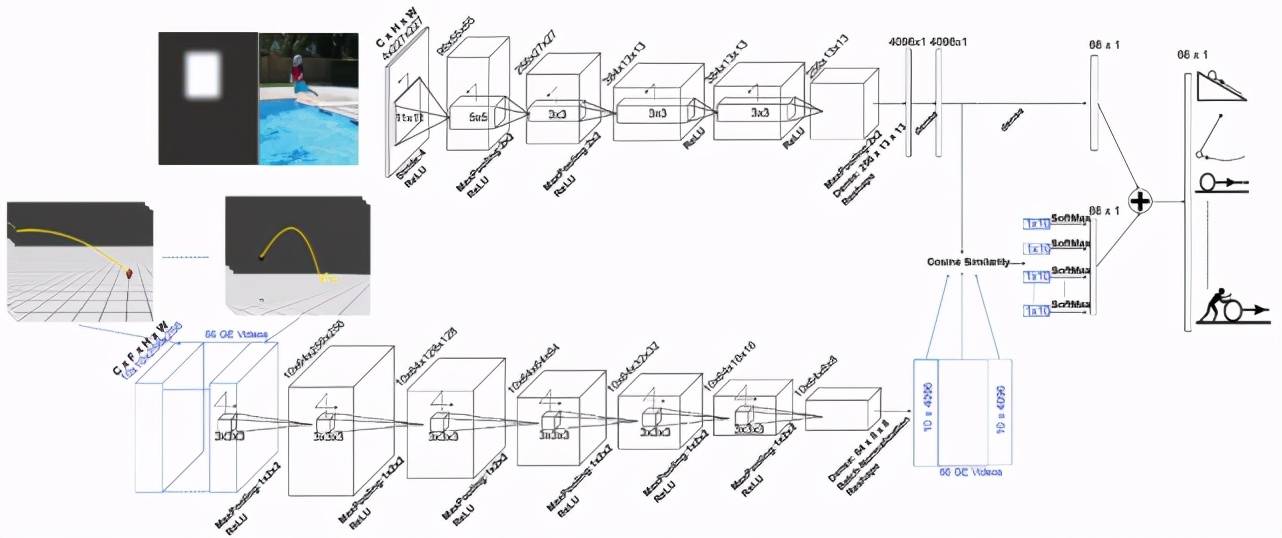
图 6 给出 N^ 3 的示意图。 N^ 3由两个平行的卷积神经网络（CNNs）组成，其中一个用来编码视觉线索，另一个用来表示牛顿运动。 N^ 3的输入是一个带有四个通道的静态图像（RGBM ，其中 M 是对象掩码通道，通过使用高斯核平滑的边界框掩码指定查询对象的位置）和 66 个牛顿假设视频，其中每个视频有 10 帧（从整个视频中采样的等距帧），每个帧有 10 个通道（表示 RGB、流、深度和曲面法线）。 N^ 3的输出是一个 66 维向量，其中每个维度表示分配给牛顿假设视点的输入图像的置信度。 N^ 3通过强制静态图像的向量表示和对应于牛顿假设的视频帧的向量表示之间的相似性来学习映射。状态预测是通过在牛顿空间中寻找与静态图像最相似的帧来实现的。
【碰撞|深度学习如何学习直观物理学】第一行（编码视觉线索）类似于文献 [6] 中介绍的用于图像分类的标准 CNN 架构。我们将这一行称为图像行。图像行有五个 2D CONV 层（卷积层）和两个 FC 层（全连接层）。第二行表示牛顿运动的网络，是受 [7] 启发的体积卷积神经网络（Volumetric convolutional neural network）。我们把这一行称为运动行。运动行有六个 3D CONV 层和一个 FC 。运动行的输入是一批 66 个视频（对应于游戏引擎渲染的 66 个牛顿假设）。运动行生成 4096x10 的矩阵作为每个视频的输出，其中该矩阵中的一列可视为视频中帧的描述符。为了在输出中保持相同的帧数，作者消除了运动行中所有 CONV 层在时间维度上的 MaxPooling 。这两行由匹配层连接起来，匹配层使用余弦相似性作为匹配度量。图像行的输入是 RGBM 图像，输出是 4096 维向量（FC7 层之后的值）。这个向量可以看作是输入图像的视觉描述符。匹配层以图像行的输出和运动行的输出作为输入，计算图像描述符与该批视频中所有 10 帧描述符之间的余弦相似度。因此，匹配层的输出是 66 个向量，每个向量有 10 维。具有最大相似值的维数表示每个牛顿假设的动力学状态。例如，如果第三维具有最大值，则意味着输入图像与游戏引擎视频的第三帧具有最大相似性，因此其必须具有与相应游戏引擎视频中的第三帧相同的状态。在余弦相似层之后附加一个 SoftMax 层，以选取最大相似性作为每个牛顿假设的置信分数。这使得N^ 3能够在没有任何状态级注释的情况下学习状态预测。这是N^ 3的一个优势，它可以通过直接优化牛顿假设的预测来隐式地学习运动状态。这些置信度分数与来自图像行的置信度分数线性组合以产生最终分数。

文章图片

图 6. N^ 3示意图
1.1.3 实验分析
作者使用 Blender 游戏引擎渲染对应于 12 个牛顿假设的游戏引擎视频。给定一幅图像和一个查询对象，作者评估本文方法估计对象运动的能力。表 1 列出了一组与若干基线方法的比较结果。第一个基线称为直接回归（Direct Regression），是从图像到三维空间中轨迹的直接回归（ground-truth 曲线由 1200 节的 B 样条曲线表示）。对于这个基线，作者修改了 AlexNet 架构，使每个图像回归到其相应的 3D 曲线。表 1 显示， N^ 3显著优于这一基线方法。作者假设这主要是由于输出的维度以及微小视觉线索和物体的三维运动之间复杂的相互作用。
为了进一步探索直接回归是否可以粗略估计轨迹形状的问题，作者建立了一个更强大的基线 ----“直接回归 - 最近（Direct Regression-Nearest）” ，使用上述直接回归基线的输出来寻找牛顿假设中最相似的 3D 曲线（基于 B 样条表示之间的标准化欧氏距离）。表 1 显示， N^ 3也优于这一基线方法。

文章图片

表 1. 三维物体运动的估计，采用 F - 测度作为评价指标
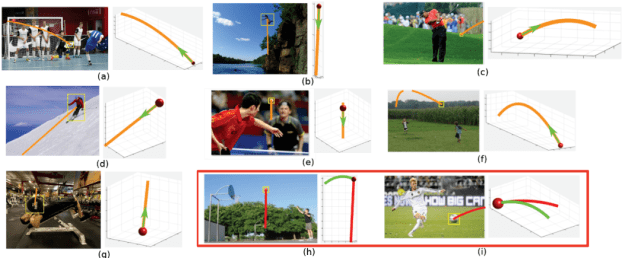
图 7 给出了在静止图像中估计对象预期运动的定性实验结果。当N^ 3预测图像的 3D 曲线时，它也会估计视点。这使我们能够将 3D 曲线投影回图像上。图 7 给出了这些估计运动的示例。例如， N^ 3正确地预测了足球投掷的运动（图 7（f）），并估计了乒乓球下落的正确运动（图 7（e））。请注意， N^ 3无法解释将来可能与场景中其他元素发生的碰撞。例如，图 7（a）给出足球运动员的预测运动。此图还显示了一些失败的示例。图 7（h）中的错误可能是由于球员与篮球之间的距离过大。当我们将 3D 曲线投影到图像时，还需要假设到相机的距离， 2D 投影曲线的比例可能不一致。

文章图片

图 7. 橙色显示静态图像中对象的预期运动。作者可视化了物体的三维运动（红色球体）及其在图像上的叠加（左图），红框中还显示了失败案例，其中红色和绿色曲线分别表示本文预测结果和真实情况
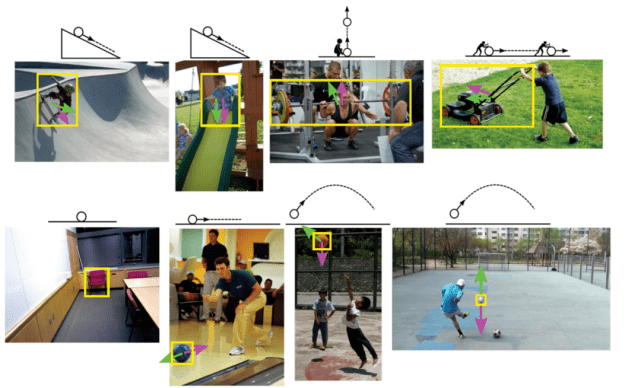
有趣的是， N^ 3还可以预测查询对象静态图像中合力（Net force）和速度的方向！图 8 给出了定性示例。例如， N^ 3可以预测保龄球示例中的摩擦力以及篮球示例中的重力。由于地板的法向力抵消了重力，所以施加在最下面一排（左）椅子上的合力为零。

文章图片

图 8. 合力方向和物体速度可视化展示。速度以绿色显示，合力以红色显示。相应的牛顿假设显示在每张图片的上方
1.2 Visual Stability Prediction and Its Application to Manipulation [3]
https://arxiv.org/abs/1609.04861
1.2.1 基本思路
婴儿在很小的时候就能够通过观察获得关于物理事件的知识。例如，支撑：一个物体如何稳定地抓住另一个物体；碰撞：一个移动的物体如何与另一个物体相互作用。根据他们的研究，婴儿或许具有先天能力的通过观察身体事件的各种结果，能够逐渐建立起自身身体事件的内部模型。婴儿先天具备的物理事件的基本知识，例如对支撑现象的理解，可以使其完成对相对复杂的构造结构的操作。这种结构是通过堆叠一个元件或移除一个元件而产生的，同时主要依靠对这种玩具结构中支撑事件的有效了解来保持结构的稳定性。在本文工作中，作者针对这个支撑事件，建立了一个机器学习模型（视觉稳定性分类器)来预测堆叠对象的稳定性。
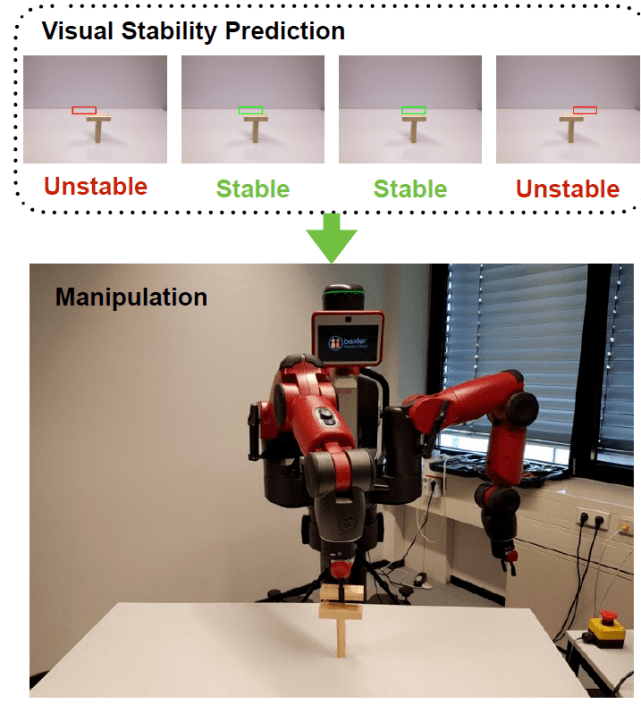
作者通过在一系列条件下，包括不同数量的木块、不同的木块尺寸、平面与多层结构等，综合生成一组大木块塔来解决预测稳定性的问题。通过模拟器运行这些配置（仅在训练时！）以便生成塔是否会倒塌的标签。此外，作者还应用该方法指导机器人堆叠木块。为了避免合成图像和真实场景图像之间的域偏移，作者提取了合成图像和捕获图像的前景掩模（Foreground mask）。给定一个真实的块结构，机器人使用训练在合成数据上的模型（视觉稳定性分类器)来预测可能的候选位置的稳定性结果，然后对可行的位置进行叠加。如图 9 所示，作者构建了一个试验台， Baxter 机器人的任务是在给定的木块结构上堆叠一个木块，而不破坏结构的稳定性。

文章图片

图 9. 给定一个木块结构，视觉稳定性分类器预测未来放置的稳定性，然后机器人会在预测的稳定放置中堆叠一个木块
1.2.2 视觉稳定性预测

文章图片

图 10. 学习视觉稳定性方法概述。需要注意的是，物理引擎只在训练时用于获取 groung-truth 来训练深度神经网络，而在测试时，只给学习模型提供渲染的场景图像来预测场景的物理稳定性
首先，图 10 中给出了视觉稳定性方法的整体结构。本文实验中生成以长方体块为基本元素的合成数据。在不同的场景中，块数、块大小和叠加深度是不同的，我们称之为场景参数。
a）块数量：通过改变塔的大小来影响任务难度，并挑战塔在人类和机器中的稳定性。显然，随着块数的增加，接触面和相互作用的数量增多，使问题越来越复杂。因此，我们将具有四个不同块数的场景设置为{4B,6B , 10B, 14B} ，即 4 块、6 块、10 块和 14 块。
b）叠加深度：当研究目的是从单目输入判断稳定性时，作者改变了塔的深度，从单层设置（称之为 2D）到多层设置（称之为 3D）。第一层设置仅允许沿图像平面在所有高度级别上叠加单个块，而另一层不强制执行此类约束，并且可以在图像平面中展开。如表 2 所示。
c）块大小：本文实验包括了两组块大小设置。在第一种设置中，塔是由大小都为 1 x1 x 3 的块构成的。第二种设置中引入了不同的块大小，其中三个维度中的两个是随机缩放的，随机分布满足 [1-δ, 1+δ] 附近的截断正态分布（Truncated Normal Distribution）N(1, σ^2) 。这两种设置表示为{Uni, NonUni} 。第二种设置中引入了非常微小的视觉线索，整个塔的稳定性取决于不同大小的块之间的小间隙。这种任务对于人类来说都是非常有难度的。
d）场景：结合这三个场景参数，作者定义了 16 个不同的场景组。例如，组 10B-2D-Uni 表示使用相同大小的 10 个块堆叠在单个层中的场景。对于每个场景组，生成 1000 个候选场景，其中每个候选场景都以自底向上的方式用不重叠的几何约束构造。总共有 16K 个场景。
e）渲染：本实验中不使用彩色砖块，从而使得识别砖块轮廓和配置的任务更有挑战性。整个场景的照明固定、摄像机自动调整，从而保证塔位于拍摄图像的中心。图像以 800 x 800 的彩色分辨率渲染。
f）物理引擎：使用 Panda3D 中的 Bullet 完成每个场景在 1000Hz 下 2 秒的物理模拟。在模拟中启用了表面摩擦和重力。系统记录时刻 t 内一个场景中的 N 个块为(p_1, p_2,..., p_N)_t ，其中 p_i 为块 i 的位置。然后将稳定性自动确定为布尔变量：

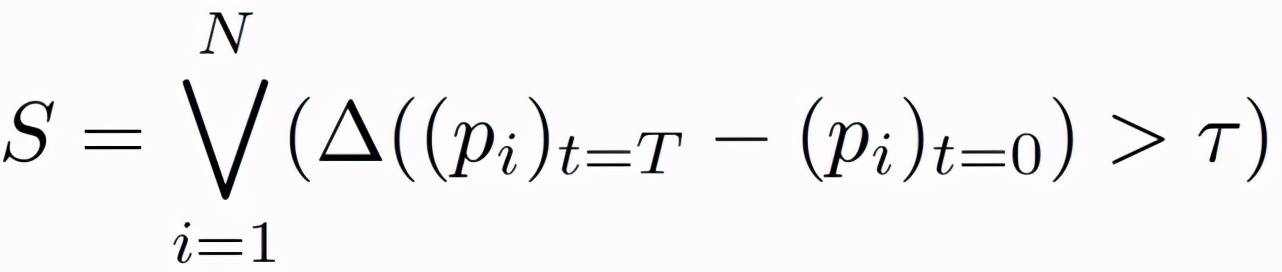
文章图片

其中， T 表示模拟的结束时间， Δ用于衡量起始和结束时间之间块的位移情况， τ为位移阈值， V 表示逻辑或。计算的结果 True 或 False 表示这个场景是 “不稳定” 或者“稳定” 。
对于人类来说，不管其解析视觉输入的实际内在机制如何，很明显存在一个涉及视觉输入 I 到稳定性预测 P 的映射 f：

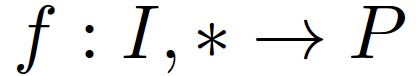
文章图片

其中， * 表示其它可能的信息。
在本文工作中，感兴趣的是 f 到视觉输入的映射，并直接预测物理稳定性。作者使用了深度卷积神经网络，因为它在图像分类任务中的应用效果非常好。这种网络通过重新训练或微调自适应，能够适应广泛的分类和预测任务。因此，作者认为它是研究视觉预测这一具有挑战性的任务的适当方法。
作者使用 LeNet（一个相对较小的数字识别网络）、AlexNet（一个较大的网络）和 VGG-Net（一个比 AlexNet 更大的网络）对生成的数据子集进行了测试。作者发现在测试过程中 VGG 网络始终优于其他两个，因此本文最终使用的深度学习方法是 VGG ，且所有的实验中都使用了 Caffe 框架。

文章图片

表 2. 渲染场景中的场景参数概述。有 3 组场景参数，包括块数、叠加深度和块大小
为了评估任务的可行性，作者首先在具有相同场景参数的场景上进行训练和测试，称为组内实验（Intra-Group Experiment），实验结果见表 3 。在这组实验中，固定叠加深度且保持场景中所有块的大小相同，但改变场景中块的数量，以观察该参数对图像训练模型预测率的影响。在不同的块大小和堆叠深度条件下，随着场景中块数的增加，可以观察到稳定性能在持续下降。场景中的块越多，通常导致场景结构塔的高度越高，因此感知难度就越大。此外，作者还探讨了相同大小和不同大小的块如何影响图像训练模型的预测率，当从 2D 堆叠移动到 3D 堆叠时，稳定性能会下降。块大小带来的额外变化确实加大了稳定性任务的难度。最后，作者研究了堆叠深度对预测率的影响。随着堆叠深度的增加，对场景结构的感知越来越困难，场景的某些部分可能被其他部分遮挡或部分遮挡。对于简单场景，当从 2D 堆叠移动到 3D 时，预测精度提高，而对于复杂场景则是相反的。

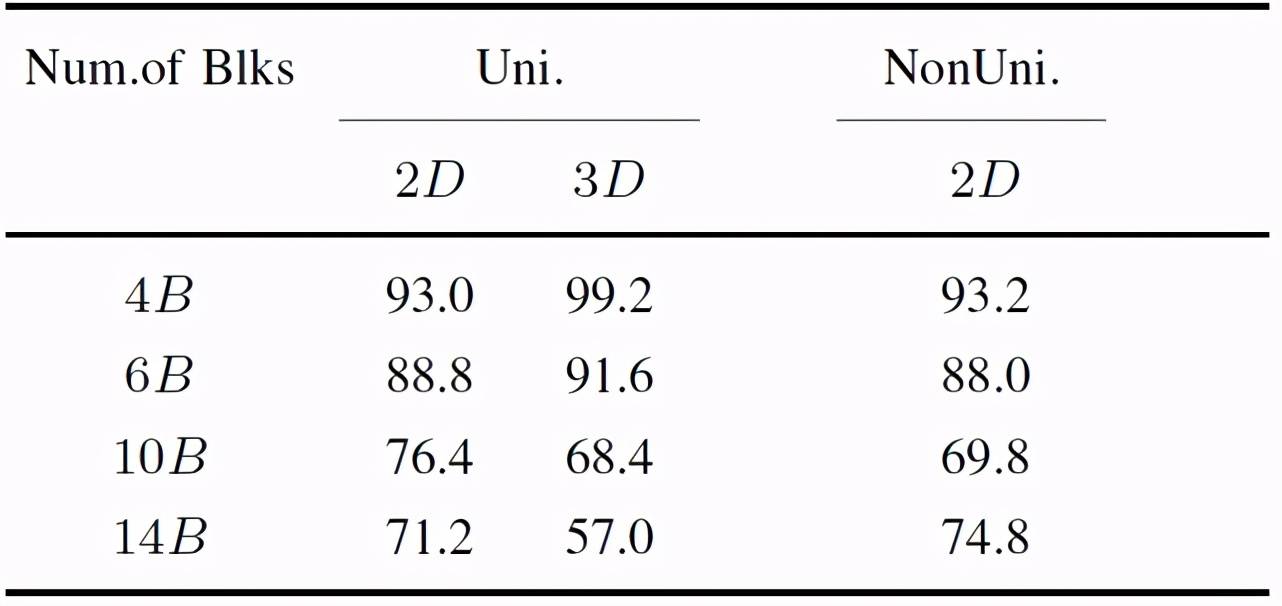
文章图片

表 3. 组内实验结果
为了进一步了解模型如何在具有不同复杂度的场景之间变化，作者根据块数将场景组分为两大组，进行组间实验（Cross-Group Experiment），包括一个具有 4 和 6 个块的简单场景组和一个具有 10 和 14 个块的复杂场景组。实验结果见表 4 。作者对简单场景进行训练，对复杂场景进行预测，最终预测率为 69.9% ，明显优于 50% 的随机猜测。作者认为这是因为学习的视觉特征可以在不同的场景中传递。此外，在复杂场景中训练并对简单场景进行预测时，模型的性能显著提高。作者分析这可能是由于模型能够从复杂场景中学习到更丰富和更好的泛化特征。

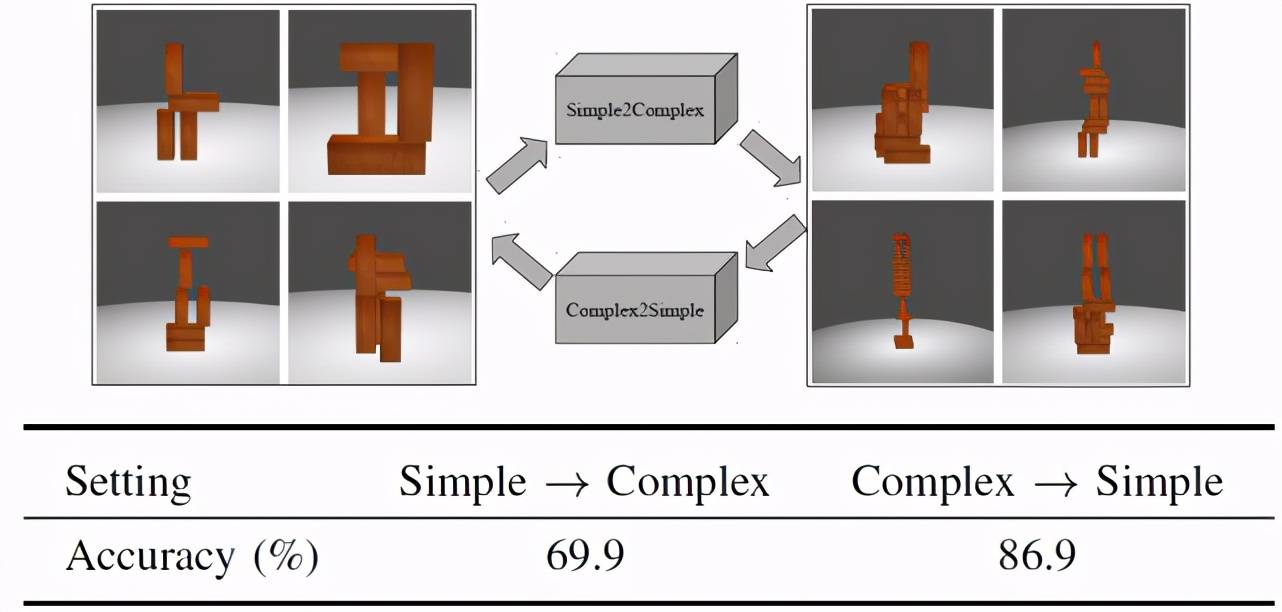
文章图片

表 4. 组间实验结果
1.2.3 操作控制（Manipulation）
进一步，作者探索合成数据训练模型是否以及如何用于实际应用，特别是用于机器人操作控制中。因此，作者建立了一个如图 9 所示的试验台， Baxter 机器人的任务是在给定的木块结构上堆叠一个木块，而不破坏结构的稳定性。该实验系统的完整结果如图 12 。实验中使用 Kapla 块作为基本单元，并将 6 个块粘贴到一个较大的块中，如图 13a 所示。为了简化任务，作者对自由式堆叠进行了调整：
与上一节中的 2D 情况一样，将给定的块体结构限制为单层。在最后的测试中，作者报告了 6 个场景的结果，如表 5 所示。
将放在给定结构顶部的块限制为两个规范配置{vertical ， horizongtal} ，如图 13b 所示，并假设在放置之前是被机器人握在手中的。
将块约束为放置在给定结构的最顶层水平面（堆叠面）上。
校准结构深度（与机器人的垂直距离），这样只需要确定相对于堆叠的塔表面的水平和垂直位移。

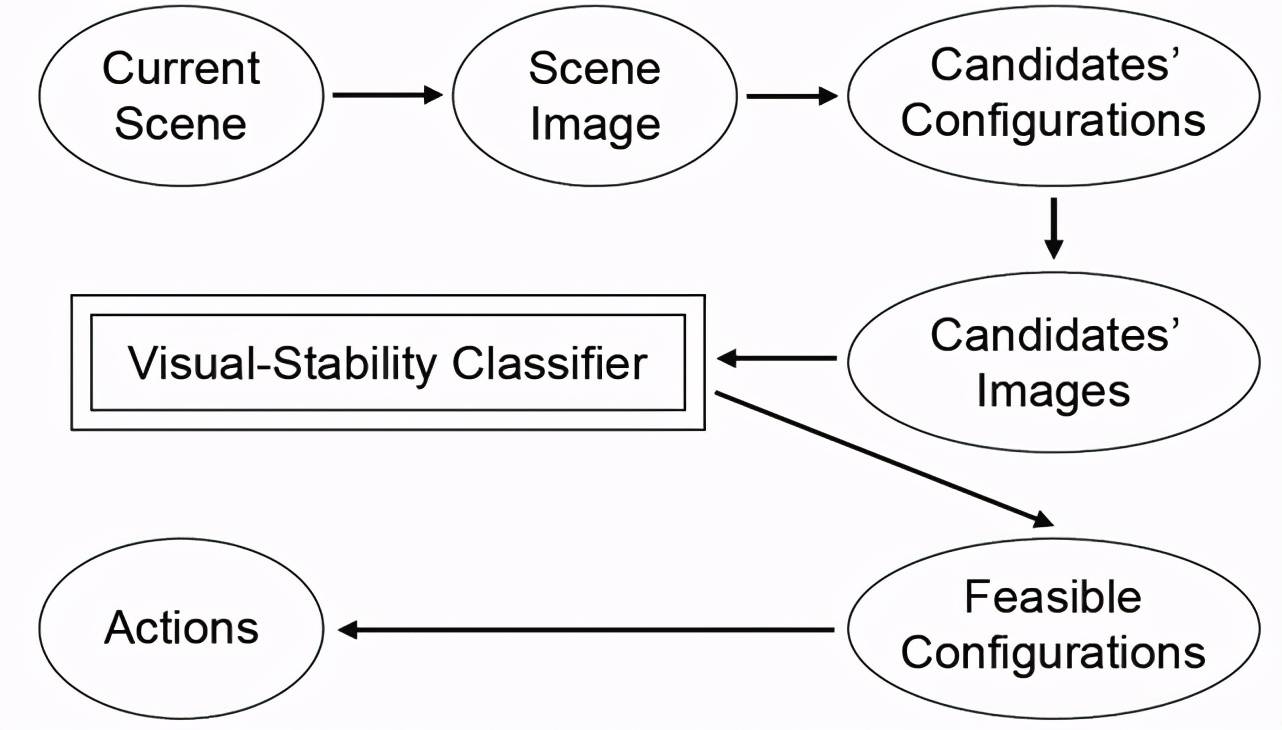
文章图片

图 12. 控制系统概览

文章图片

图 13. 实验中用到的积木
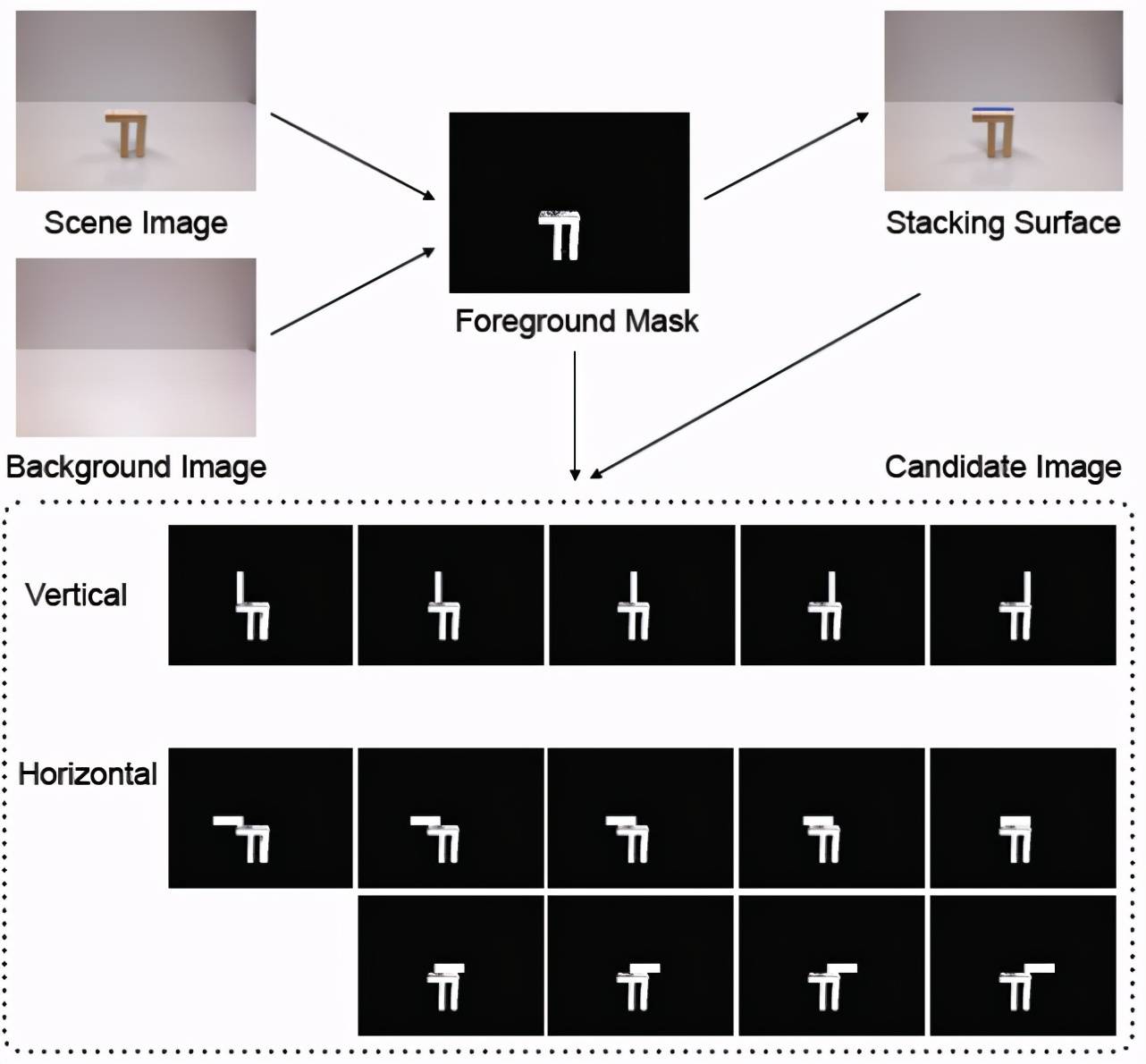
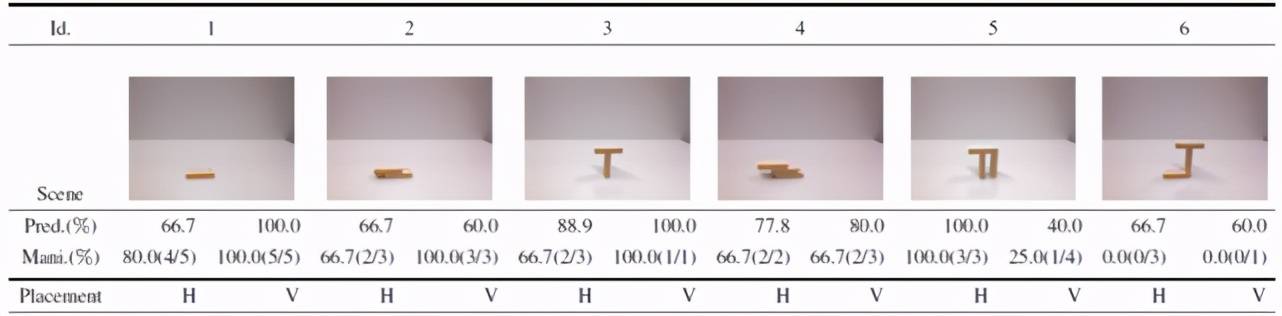
为了应对真实世界物体图片与合成数据的不同，作者在合成数据的二值前景模板上训练视觉稳定性模型，并在测试时对模板进行处理。这样，就大大降低了真实世界中彩色图片的影响。在测试时，首先为空场景捕获背景图像。然后，对于表 5 中所示的每个测试场景捕获图像并通过背景减法将其转换为前景遮罩。检测最上面的水平边界作为堆叠表面用于生成候选放置：将该表面均匀划分为 9 个水平候选和 5 个垂直候选，因此总共有 84 个候选。整个过程如图 14 所示。然后，将这些候选对象放入视觉稳定性模型中进行稳定性预测。每个生成的候选对象的实际稳定性都手动测试并记录为 ground-truth 。最终的识别结果如表 5 所示。由该表中实验结果可知，使用合成数据训练的模型能够在现实世界中以 78.6% 的总体准确率预测不同的候选对象。

文章图片

图 14. 为给定场景生成候选放置图像的过程

文章图片

表 5. 真实世界测试的结果。 “Pred.”是预测精度。 “Mani.”是操纵成功率，包括每个场景的成功放置 / 所有可能的稳定放置计数。 “H/V”指水平 / 垂直放置
1.3 Learning to Poke by Poking: Experiential Learning of Intuitive Physics [4]
https://arxiv.org/abs/1606.07419
1.3.1 基本思路
人类具备对工具进行泛化的能力：我们可以毫不费力地使用从未见过的物体。例如，如果没有锤子，人们可能会用一块石头或螺丝刀的背面来敲打钉子。是什么使人类能够轻松地完成这些任务呢？一种可能性是，人类拥有一个内在的物理模型（直观物理），使他们能够对物体的物理特性进行推理，并预测其在外力作用下的动态。这样的模型可以用来把一个给定的任务转换成一个搜索问题，其方式类似于在国际象棋或 tic-tac-toe 游戏中通过搜索游戏树来规划移动路径。由于搜索算法与任务语义无关，因此可以使用相同的机制来确定不同任务（可能是新任务）的解决方案。
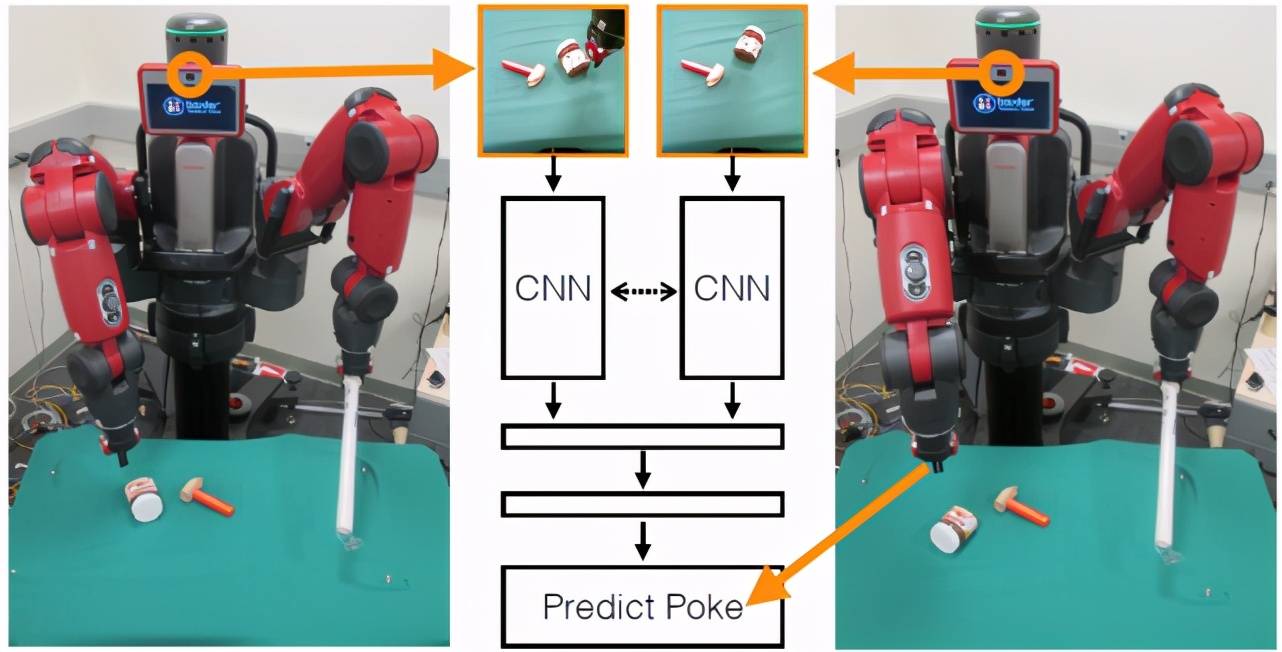
小婴儿在成长的过程中总是会以一种看似随机的方式玩东西，他们并没有明确的“目标” 。关于婴儿这种行为的一种假设是婴儿将这种经验提炼成了直观物理模型，预测他们的行为如何影响物体的运动。一旦学会了，他们就可以利用这些模型规划行动，以应对新的出现在生活中的物体。受这一假设的启发，本文研究了机器人是否也可以利用自己的经验来学习一个直观的有效物理模型。在图 15 所示的任务场景中， Baxter 机器人通过随机戳（Poke）放在它前面桌上的物体来与它们互动。机器人在 Poke 之前和之后记录视觉状态，以便学习其动作与由物体运动引起的视觉状态变化之间的映射。到目前为止，本文的机器人已经与物体进行了 400 多个小时的互动，并在这个过程中收集了超过 10 万个不同物体上的 Poke 。机器人配备了 Kinect 摄像头和一个夹子，用来戳放在它前面桌子上的物体。在给定的时间内，机器人从桌上 16 个不同的目标对象中选择 1-3 个对象。机器人的坐标系为：X 轴和 Y 轴分别代表水平轴和垂直轴， Z 轴则指向远离机器人的方向。机器人通过用手指沿着 XZ 平面从桌子上移动一个固定的高度来戳物体。
为了收集交互数据的样本，机器人首先在其视野中选择一个随机的目标点来戳。随机戳的一个问题是，大多数戳是在自由空间中执行的，这严重减慢了有效交互数据的收集过程。为了快速收集数据，作者使用 Kinect 深度相机的点云只选择位于除桌子以外的任何对象上的点。点云信息仅在数据采集阶段使用，在测试时，本文的系统只需要使用 RGB 图像数据。在对象中随机确定一个点 poke(p) ，机器人随机采样 poke 的方向 (θ) 和长度(l) 。
这个机器人可以无需任何人工干预的全天候自主运行。有时当物体被戳到时，它们会按预期移动，但有时由于机器人手指和物体之间的非线性交互作用，它们会以意外的方式移动，如图 16 所示。所以模型必须能够处理这种非线性交互。项目早期的少量数据是在一张背景为绿色的桌子上收集的，但实际上绝大部分数据是在一个有墙的木制区域中收集的，主要目的是防止物体坠落。本文的所有结果都来自于从木制区域收集的数据。

文章图片

图 15. 机器人通过随机戳来与物体互动。机器人戳物体并记录戳前（左图）和戳后（右图）的视觉状态。利用前图像、后图像和应用 poke 的三元组训练神经网络（中间图），学习动作与视觉状态变化之间的映射关系

文章图片

图 16. 这些图像描绘了机器人将瓶子从指示虚线移开的过程。在戳的中间，物体会翻转，最后朝着错误的方向移动。这种情况很常见，因为现实世界中的对象具有复杂的几何和材质特性
1.3.2 模型分析
机器人应该从经验中学习什么样的模型？一种可能性是建立一个模型，根据当前的视觉状态和施加的力来预测下一个视觉状态（即正向动力学模型）。本文提出了一个联合训练正向和反向动力学模型。正向模型根据当前状态和动作预测下一个状态，反向模型根据初始状态和目标状态预测动作。在联合训练中，反向模型目标提供监督，将图像像素转化为抽象的特征空间，然后由正向模型预测。反向模型减轻了正向模型在像素空间中进行预测的需要，而正向模型反过来又使反向模型的特征空间正则化。
使用公式（1）和公式（2）分别定义正向、反向模型：

文章图片

其中， x_t, u_t 分别表示应用于时间步长 t 的世界状态和动作， ^x_t+1, ^u_t+1 是预测的状态和动作， W_fwd 和 W_inv 是用于构建正向和反向模型的函数 F 和 G 的参数。给定初始状态和目标状态，反向模型给出了映射到直接能够实现目标状态所需的操作（如果可行的话）。然而，多种可能的行为可能将当前的世界状态从一种视觉状态转换为另一种视觉状态。例如，如果 agent 移动或 agent 使用其手臂移动对象，则对象可能出现在机器人视野的某个部分。行动空间中的这种多模态使得学习变得非常困难。另一方面，给定 x_t 和 u_t ，存在下一状态 x_t+1 ，该状态对于动力学噪声是唯一的。这表明正向模型可能更容易学习。
然而，在图像空间学习正向模型是很困难的，因为预测未来帧中每个像素的值是非常困难的。在大多数场景中，我们对预测具体的像素不感兴趣，而是希望能够预测更抽象事件的发生，例如对象运动、对象姿势的变化等。使用正向模型的第二个问题是，推断最优行为不可避免地会导致找到受局部最优约束的非凸问题的解。而反向模型就没有这个缺点，因为它直接输出所需的动作。这些分析表明，反向模型和正向模型具有互补的优势，因此有必要研究反向模型和正向动力学的联合模型。
本文使用的学习正向和反向动力学的联合深度神经网络如图 17 所示。

文章图片

图 17. 联合深度神经网络示例
训练样本包括一组前图像 (I_t)、后图像(I_t+1) 和机器人动作 (u_t) 。在随后的时间步长(I_t,I_t+1) 内将样本输入五个卷积层以得到潜在特征表示 (x_t, x_t+1) ，这五个卷积层与 AlexNet 的前五层结构相同。为了建立反向模型，串联 x_t,x_t+1 并通过全连接层来有条件地分别预测戳的位置(p_t)、角度(θ_t) 和长度 (l_t) 。为了模拟多模态戳分布，将戳的位置、角度和长度分别离散化为 20x 20 的网格、36 个 bins 和 11 个 bins 。戳长度的第 11 个 bin 用于表示没有戳（no poke）。为了建立正向模型，将正向图像的特征表示(x_t) 和动作（u_t ，未离散化的实值向量）传递到一个全连接层序列中，该序列预测下一幅图像 (x_t+1) 的特征表示。优化下式中的损失以完成训练：

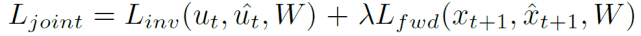
文章图片

其中， L_inv 为真实和预测的戳位置、角度和长度的交叉熵损失和。 L_fwd 为预测和 ground-truth 之间的 L1 损失。 W 为神经网络的权重。
测试该模型的一种方法是向机器人提供初始图像和目标图像，并要求它进行戳的动作将物体移动到目标图像显示的位置中。当初始图像和目标图像对的视觉统计与训练集中的前后图像相似时，机器人就成功地完成了动作。如果机器人能够将物体移动到目标位置，而目标位置与物体在一次戳之前和之后的位置相比相距更远，作者认为这表明该模型可能了解了物体在被戳时如何移动的基本物理原理。如果机器人能够在多个干扰物存在的情况下推动具有几何形状和纹理复杂的物体，则说明模型的能力更强。如果初始图像和目标图像中的对象之间的距离超过了单个戳的动作可以推的最大距离，则需要模型输出一系列戳。作者使用贪婪计划方法（见图 18（a））来输出戳序列。首先，描述初始状态和目标状态的图像通过该模型来预测戳，由机器人执行。然后，将描述当前世界状态的图像（即当前图像）和目标图像再次输入到模型中以输出戳。重复此过程，当机器人预测无戳或达到 10 个戳时结束。
在所有的实验中，初始图像和目标图像只有一个物体的位置是不同的。将机器人停止后最终图像中物体的位置和姿态与目标图像比较后进行定量评价。通过计算两张图像中物体位置之间的欧氏距离来得到位置误差。在初始状态和目标状态下，为了考虑不同的目标距离，作者使用相对位置误差代替绝对位置误差。姿态误差则定义为最终图像和目标图像中物体长轴之间的角度（以度为单位）（见图 18（c））。

文章图片

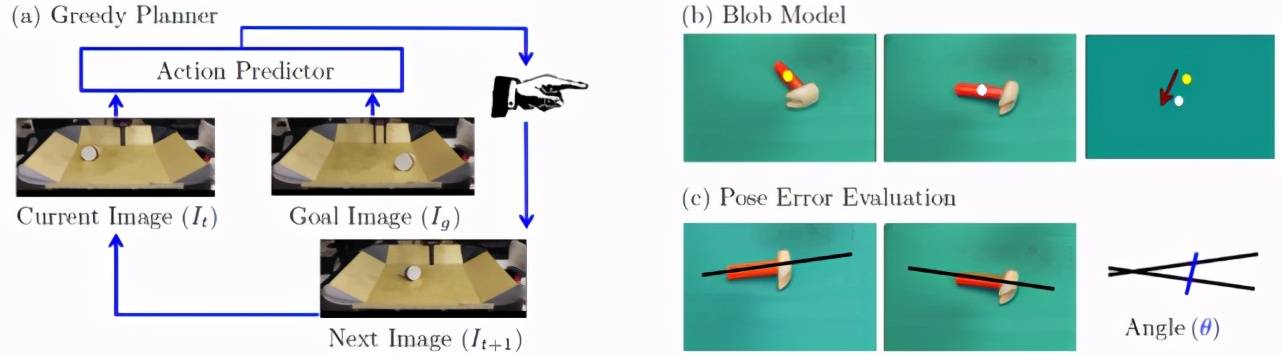
图 18. （a）贪婪规划算子用于输出一系列戳，以将对象从初始配置置换到目标图像。（b） blob 模型首先检测对象在当前图像和目标图像中的位置。根据物体的位置，计算出戳的位置和角度，然后由机器人执行。利用得到的下一帧图像和目标图像来计算再下一帧图像，并迭代地重复这个过程。（c）模型将物体戳到正确姿势的误差度量为最终图像和目标图像中物体长轴之间的夹角
本文作者选择 blob 模型作为基线对比模型（图 18（b））。该模型首先利用基于模板的目标检测器估计目标在当前图像和目标图像中的位置。然后，它使用这两者之间的向量差来计算机器人执行的戳的位置、角度和长度。以类似于对学习模型进行贪婪规划的方式，迭代地重复此过程，直到对象通过预定义的阈值更接近目标图像中的所需位置或达到最大戳数。
1.3.3 实验分析
本文实验中机器人的任务是将初始图像中的物体移动到目标图像描述的形状中（见图 19）。图 19 中的三行显示了当要求机器人移动训练集中的对象（Nutella 瓶）、几何结构与训练集中的对象不同的对象（红杯子）以及当任务是绕障碍物移动对象时的性能。这些例子能够表征机器人的性能，可以看出，机器人能够成功地将训练集中存在的对象以及复杂的新的几何结构和纹理的对象戳入目标位置，这些目标位置明显比训练集中使用的一对前、后图像更远。更多的例子可以在项目网站上找到（http://ashvin.me/pokebot-website/）。图 19 中的第 2 行还显示，在当前图像和目标图像中占据相同位置的干预物体的存在并不会影响机器人的性能。这些结果表明，本文模型允许机器人执行超出训练集的泛化任务（即小距离戳物体）。图 19 中的第 3 行给出了一个机器人无法将物体推过障碍物（黄色物体）的例子。机器人贪婪地行动，最后的结果是一起推障碍物和物体。贪婪规划的另一个副作用是使得物体在初始位置和目标位置之间的运动轨迹呈现锯齿形而不是直线轨迹。

文章图片

图 19. 机器人能够成功地将训练集中的物体（第 1 行；Nutella 瓶）和未知几何体物体（第 2 行；红杯）移动到目标位置，这些目标位置比训练集中使用的一对前、后图像要远得多。机器人无法推动物体绕过障碍物（第 3 行；贪婪规划限制）
机器人究竟是怎么做到的呢？作者分析，一种可能是机器人忽略了物体的几何结构，只推断出物体在初始图像和目标图像中的位置，并使用物体位置之间的差向量来推断要执行的动作。当然，这并不能证明模型已经学会目标检测了。不过作者认为其所学习的特征空间的最近邻可视化结果能够表明它对于目标位置是敏感的。不同的物体有不同的几何形状，所以为了能够以相同的方式移动它们，就需要在不同的地方戳它们。例如，对于 Nutella 瓶子来说，不需要旋转瓶子，只需要沿着朝向其质心的方向在侧面戳瓶子。对于锤子来说，移动它的方法则是在锤头与手柄接触的地方戳。
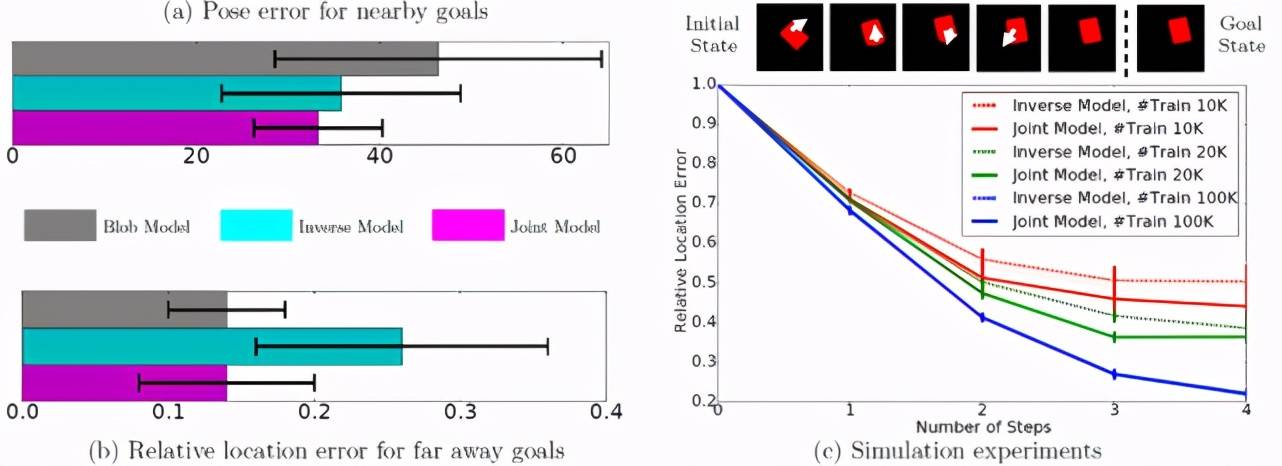
与将对象推到所需位置相比，将对象推到所需姿势更困难，需要更详细地了解对象几何特征。为了测试学习到的模型是否能够表征与对象几何特征有关的信息，作者将其性能与忽略对象几何特征的基线 Blob 模型（见图 18（b））进行了比较。在这个对比实验中，机器人的任务是只戳一次就把物体推到附近的目标。图 20（a）中的结果表明，反向模型和联合模型都优于 blob 模型。这表明除了能够表征对象位置的信息外，本文的模型还能够表征对象几何特征相关的信息。
在二维仿真环境中，作者还检验了正向模型是否正则化了反向模型学习到的特征空间。在二维仿真环境中，机器人使用较小的力量戳一个红色矩形物体来与之交互。允许矩形自由平移和旋转（图 20（c））。图 20（c）显示，当可用的训练数据较少（10K、20K 实例）时，联合模型的性能优于反向模型，并且能够以较少的步骤（即较少的动作）接近目标状态。这表明，正向模型确实对反向模型的特征空间进行了正则化处理，从而使其具有更好地推广和泛化性能。然而，当训练实例的数量增加到 100K 时，两个模型性能相同。作者认为这是由于使用更多数据的训练通常直接就能够导致较好的泛化性能，此时反向模型不再依赖于正向模型的正则化处理。

文章图片

图 20. （a）反向模型和联合模型在将物体推向所需姿势时比 blob 模型更精确；（b）当机器人在训练集使用的前后图像中按明显大于物体距离的距离推动物体时，联合模型的性能优于纯反向模型；（c）当训练样本数较少（10K、20K）时，联合模型的性能优于反向模型，且与较大的数据量（100K）相当
1.4 Learning Intuitive Physics with Multimodal Generative Models [5]
https://arxiv.org/abs/2101.04454
1.4.1 基本思路
人类如何通过对物体初始状态的视觉和触觉测量来预测其未来的运动？如果一个以前从来没见过的物体落入手中，我们可以推断出这个物体的类别，猜测它的一些物理性质，之后判断它是否会安全地停在我们的手掌中，或者我们是否需要调整对这个物体的抓握来保持与其接触。视觉（Vision）允许人类快速索引来捕捉物体的整体特性，而接触点的触觉信号可以使人对平衡、接触力和滑动进行直接的物理推理。这些信号的组合使得人类能够预测对象的运动，即通过触觉和视觉感知物体的初始状态，预测物体被动物理动力学（Passive Physical Dynamics）的最终稳定结果。
前期研究结果表明，由于相互作用表面的未知摩擦、未知几何特征以及不确定的压力分布等因素，预测运动物体的运动轨迹非常困难。本文重点研究学习一个预测器，训练它捕捉运动轨迹中最有用和最稳定的元素。如图 21 所示，当预测对瓶子施加推力的结果时，预测器应该能够考虑这个动作最主要的后果：瓶子会翻倒还是会向前移动？为了研究这个问题，作者提出了一种新的人工感知方法，它由硬件和软件两部分组成，可以测量和预测物体落在物体表面的最终静止形态。作者设计了一种能够同时捕捉视觉图像和提供触觉测量的新型传感器 ---- 穿透皮肤（See-Through-your-Skin ， STS）传感器，同时使用一个多模态感知系统的启发多模态变分自动编码器（Multimodal variational autoencoder ， MVAE）解释 STS 的数据。

文章图片

图 21. 预测物理相互作用的结果。给定瓶子上的外部扰动，我们如何预测瓶子是否会倾倒或平移？
1.4.2 模型介绍
首先介绍 STS 传感器，它能够渲染接触几何体和外部世界的双流高分辨率图像。如图 22 所示， STS 的关键特征为：
多模态感知（Multimodal Perception）。通过调节 STS 传感器的内部照明条件，可以控制传感器反射涂料涂层的透明度，从而允许传感器提供有关接触物体的视觉和触觉反馈。
高分辨率传感（High-Resolution Sensing）。视觉和触觉信号都以 1640 x 1232 的高分辨率图像给出。使用 Odeseven 的 Raspberry Pi 可变焦距相机模块，提供 160 度的视野。这会产生两个具有相同视角、参考系和分辨率的感知信号。

文章图片

图 22. STS 传感器的可视化多模态输出。使用受控的内部照明，传感器的表面可以变得透明，如左上角所示，允许相机观察外部世界。在左下图中，传感器通过保持传感器内部相对于外部明亮来提供触觉特征
STS 视觉触觉传感器由柔顺薄膜、内部照明源、反射漆层和摄像头组成。当物体被压在传感器上时，传感器内的摄像机通过 “皮肤” 捕捉视图以及柔顺薄膜的变形，并产生编码触觉信息的图像，例如接触几何结构、作用力和粘滑行为。作者使用了一种透明可控的薄膜，允许传感器提供物理交互的触觉信息和传感器外部世界的视觉信息。作者在 PyBullet 环境中为 STS 传感器开发了一个可视模拟器，该模拟器根据接触力和几何形状重建高分辨率触觉特征。利用模拟器快速生成动态场景中对象交互的大型可视化数据集，以验证感知模型的性能。模拟器通过阴影方程映射碰撞物体的几何信息：

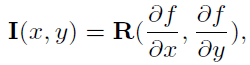
文章图片

其中， I(x,y)表示图像强度， z=f(x,y)为传感器表面的高度图， R 是模拟环境光照和表面反射率的反射函数。使用 Phong 反射模型实现反射函数 R ，该模型将每个通道的照明分为环境光、漫反射光和镜面反射光三个主要组件：

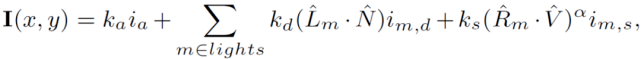
文章图片

其中， ^L_m 是从曲面点到光源 m 的方向向量， ^N 是曲面法线， ^R_m 为反射向量，

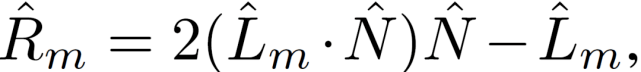
文章图片

其中， ^V 为指向摄像机的方向向量。
本文提出了一个生成性的多模态感知系统，它将视觉、触觉和 3D 姿势（如果可用）反馈集成在一个统一的框架内。作者利用多模态变分自动编码器（Multimodal Variational Autoencoders ， MVAE）来学习一个能够编码所有模态的共享潜在表示。作者进一步证明，这个嵌入空间可以编码有关物体的关键信息，如形状、颜色和相互作用力，这是对直观物理进行推断所必需的。动态交互的预测结果可以表示为一个自监督问题（Self-supervision problem），在给定框架下生成目标视觉和触觉图像。本文目标是学习一个生成器，它将当前观测值映射到静止状态的预测配置。作者认为， MVAE 结构可以用来预测多模态运动轨迹中最稳定和最有用的元素。
【变分自动编码器（Variational Autoencoders）】
生成潜在变量模型学习数据的联合分布和不可观测的表示：

文章图片

其中， p_θ(z)和 p_θ(x|z)分别表示先验分布和条件分布。目标是使边际可能性最大化：

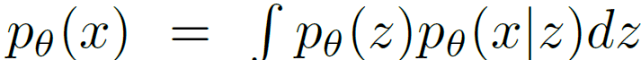
文章图片

优化的成本目标为证据下限（Evidence lower bound ， ELBO）：

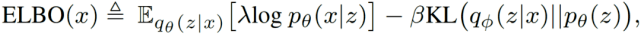
文章图片

其中，第一项表示重建损失，重建损失测量给定潜在变量的重建数据可能性的期望。第二项为近似后验值和真实后验值之间的 Kullback-Leibler 散度，在式中作用为正则化项。
【多模变分自动编码器（Multimodal Variational Autoencoders）】
VAE 使用推理网络将观测值映射到潜在空间，然后使用解码器将潜在变量映射回观测空间。虽然这种方法在恒定的观测空间中是可行的，但在多模态情况下却比较困难，这是由于观测空间的尺寸随着模态的可用性而变化。例如，触觉信息只有在与传感器接触时才可用。对于这种数据可用性上具有可变性的多模态问题，需要为每个模态子集训练一个推理网络 q(z|X) ，共产生 2^N 个组合。为了应对这个组合爆炸的问题，本文引入专家乘积模型（Product of Experts ， PoE）通过计算每个模态的个体后验概率的乘积来学习不同模态的近似联合后验概率。
多模态生成建模学习所有模态的联合分布为：

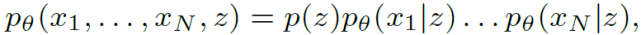
文章图片

其中， x_i 表示与模态 i 相关的观测值， N 为模态总数， z 为共享的潜在空间。假设模态之间存在条件独立性，将联合后验分布改写为：

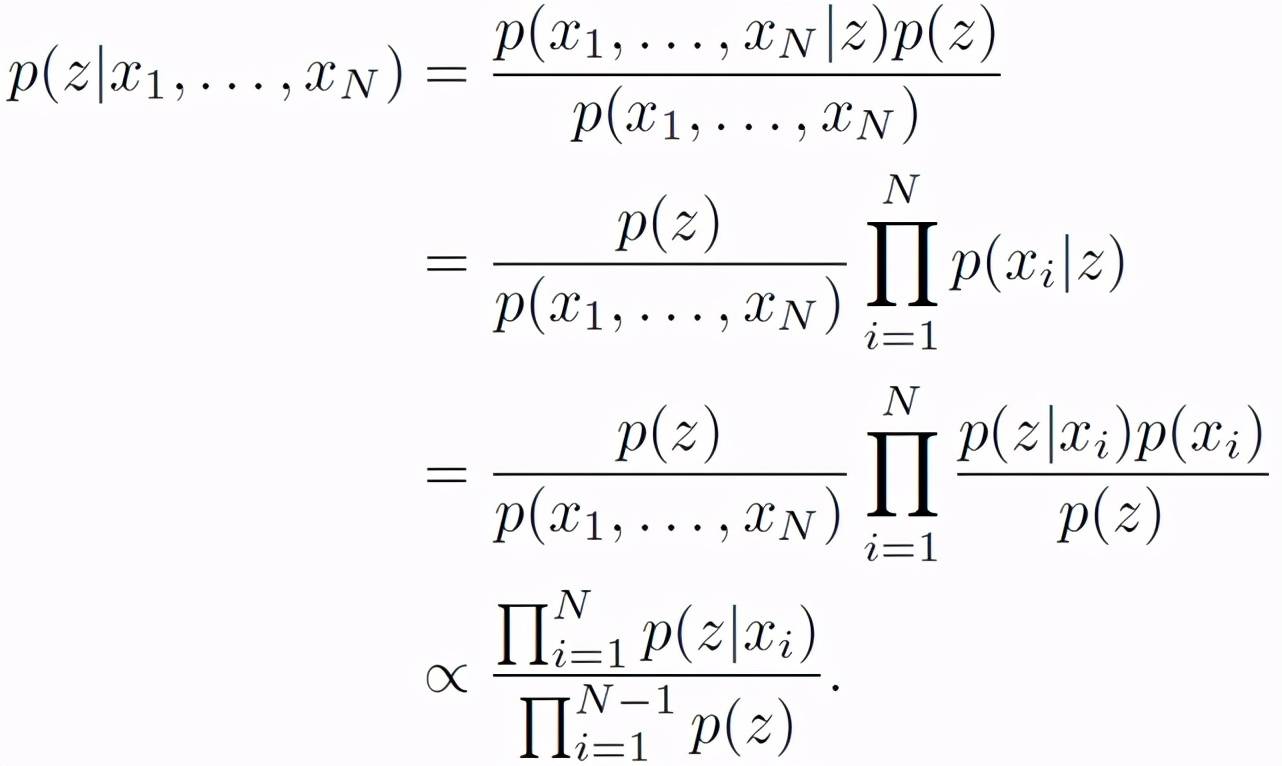
文章图片

使用模态 i 的推理网络替换上式中的 p(z|x_i) ，可得：

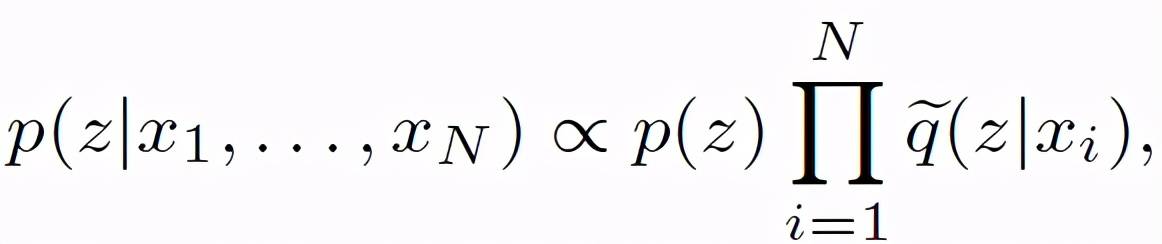
文章图片

即 PoE 。 MVAE 的一个重要优点是，与其他多模态生成模型不同，它可以有效地扩展到多种模态，因为它只需要训练 N 个推理模型，而不是 2^N 个多模态推理网络。
【用 MVAEs 学习直观物理】
作者在网络结构中引入了一个时滞元素（Time-lag element）以训练变分自动编码器，其中，将解码器的输出设置为预测未来的帧。引入 ELBO 损失：

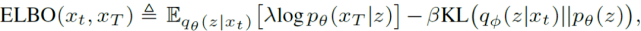
文章图片

其中， t 和 T 分别表示输入和输出时间实例。
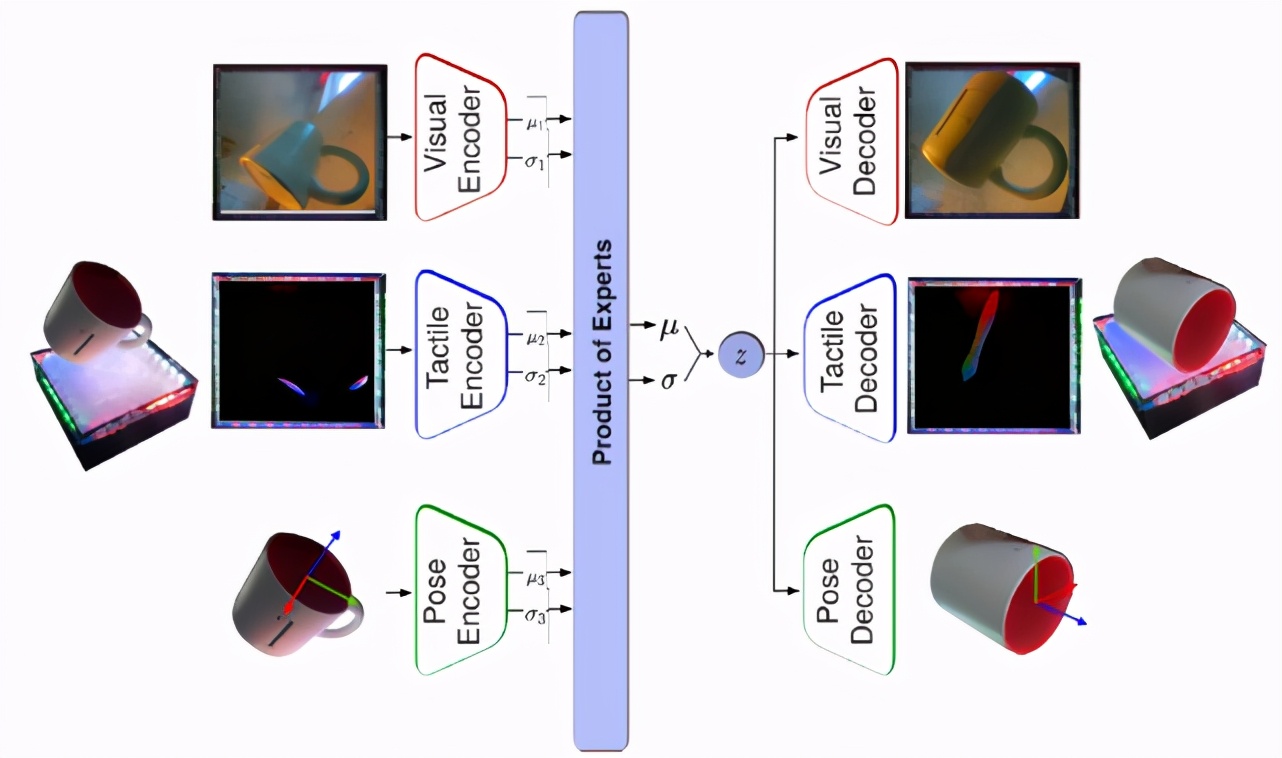
图 23 给出了动力学模型学习框架，其中视觉、触觉和 3D 姿势融合在一起，通过 PoE（product of expert）连接的三个单峰编码器 - 解码器学习共享的嵌入空间。为了训练模型损耗，作者通过列举模态 M={visual, tactile, pose}的子集来计算 ELBO 损耗：

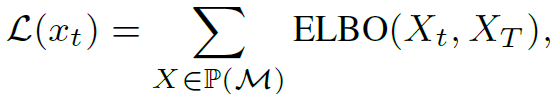
文章图片

其中， P(M)为模态集 M 的功率集。在动力学模型有输入的情况下（例如，第三个模拟场景中的力扰动），将输入条件 c 对 ELBO 损失的条件依赖性概括为：

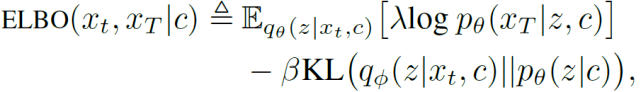
文章图片

文章图片

图 23. 多模态动力学建模。在一个统一的多模态变分自动编码器框架内集成视觉、触觉和 3D 姿态反馈的生成感知系统。网络获取当前对象配置并预测其静止配置
1.4.3 实验分析
作者使用前面描述的 PyBullet 模拟器收集模拟数据集，真实数据集则是使用 STS 传感器的原型收集的。
【模拟数据集】
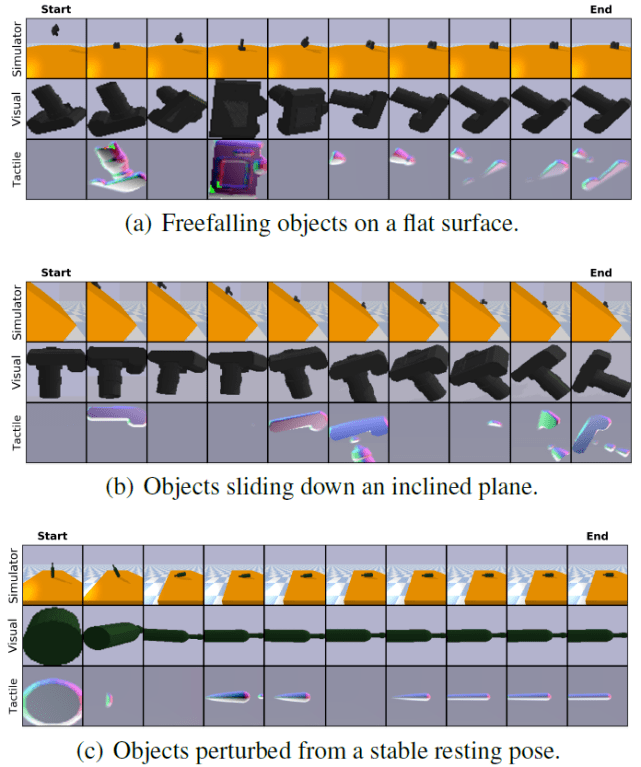
本文考虑三个模拟的物理场景，如图 24 所示，涉及从 3D ShapeNet 数据集提取的八个对象类别（bottle, camera, webcam, computer mouse, scissors, fork, spoon, watch）。具体的任务如下：
平面上自由下落的物体。这个实验在 STS 传感器上释放具有随机初始姿态的物体，在到达静止状态之前，它们与传感器发生多次碰撞。作者收集了总共 1700 个轨迹，包括 100k 图像。
从斜面上滑下来的物体。这个实验将具有随机初始姿势的物体放置在一个倾斜的表面上，在那里它们要么由于摩擦而粘住不动，要么向下滑动。向下滑动时，对象可能会滚动，此时最终状态的配置与初始状态差别非常大。作者共收集 2400 个轨迹，包括 145k 图像。
稳定的静止姿势中受到干扰的物体。在这种情况下，考虑一个物体最初稳定地停留在传感器上，它被传感器随机采样的快速横向加速度从平衡点扰动。这个实验只考虑瓶子，因为它们具有拉长的形状和不稳定的形状，在不同方向或受力大小的情况下会出现不同的实验结果。由于结果的多样性，这项任务比其他两项任务要复杂得多。作者总共收集了 2500 条轨迹，包括 150k 图像。

文章图片

图 24. 三个动态模拟场景的模拟示例片段。最上面的行显示 3D 对象视图，而中间和底部行分别显示 STS 传感器捕获的视觉和触觉测量结果
【真实数据集】
真实数据集是使用 STS 传感器手动收集的一个小的数据集。作者使用一个小型电子设备（GoPro）从 500 个轨迹中收集了 2000 张图像。之所以选择这个物体，是因为它的体积小（小到可以装在 15cm x 15cm 的传感器原型上）和质量大（重到可以在传感器上留下有意义的触觉特征）。每个轨迹都包括通过快速打开 / 关闭传感器内部灯光获得的初始和最终视觉、触觉图像。如图 25 所示，在与传感器接触的同时，将对象从不稳定的初始位置释放，一旦对象静止则确定事件结束。

文章图片

图 25. 真实世界的数据收集方法，从不稳定的初始状态释放 GoPro 相机
图 26 和 27 给出了模拟数据集的多模态预测。作者示出了 MVAE 预测物体静止形态的原始视觉和触觉测量值的能力，其预测值与 ground-truth 标签非常吻合。图 26（a）显示 MVAE 模型处理缺失模态的能力，例如触觉信息在输入中缺失不可用。该模型学习准确预测物体从传感器表面坠落的情况，产生了空输出图像。图 27 中的结果表明，该模型通过正确预测物体运动的结果（即倾倒或坠落），成功地整合了有关作用力的信息。

文章图片

图 26. 模拟数据集的三个场景中多模态预测。除了 STS 传感器的视觉和触觉测量之外，该模型还预测了最终的静止状态。最下面一行比较预测的姿态（实线坐标）和 ground-truth（虚线坐标）

文章图片

图 27. MVAE 与单模 VAE 视觉和触觉预测的定性比较
图 28 展示了该模型通过视觉和触觉图像预测静止物体形态的能力。 MVAE 与单模 VAE 的视觉预测定性结果表明， MVAE 模型利用触觉模式能够对静止形态进行更准确的推理。

文章图片

图 28. 真实数据集中 MVAE 与单模 VAE 视觉预测的定性比较
2、文章小结
这篇文章关注了深度学习如何学习直观物理学的问题。我们希望机器人也能够像人类一样根据所处的物理环境进行规划并行动。深度学习在整个过程中赋予了机器人 “学习” 的能力，因此，与经典的启发式方法、概率模拟模型相比，深度学习方法的 “学习” 能力使其能够学习并学会推断出物理属性。本文介绍了四个适用于不同场景的深度学习模型，包括 N^3 牛顿推理模型、VGG、联合训练正向和反向动力学模型、多模态变分自编码神经网络。这些模型在论文给出的实验中都表现不错，不过真实世界中的物理环境、物体运动方式、接触方式等都是非常复杂的，能够让深度学习方法真正获得类似于人类的应对物理环境的能力，还有待漫长的持续的深入研究。
本文参考引用的文献：
[1] Kubricht J R , Holyoak K J , Lu H . Intuitive Physics: Current Research and Controversies[J]. Trends in Cognitive Sciences, 2017, 21(10). http://philpapers.org/rec/KUBIPC
[2] Mottaghi R , Bagherinezhad H , Rastegari M , et al. Newtonian Image Understanding: Unfolding the Dynamics of Objects in Static Images[J]. 2015. ， http://de.arxiv.org/pdf/1511.04048
[3] Li W , Leonardis, Ale?, Fritz M . Visual Stability Prediction and Its Application to Manipulation[J]. 2016.http://arxiv.org/abs/1609.04861
[4] P Agrawal ， A Nair ， P Abbeel ， J Malik ， S Levine, Learning to Poke by Poking: Experiential Learning of Intuitive Physics,http://arxiv.org/abs/1606.07419
[5] Sahand Rezaei-Shoshtari ， Francois Robert Hogan ， Michael Jenkin ， David Meger ， Gregory Dudek, Learning Intuitive Physics with Multimodal Generative Models, https://www.researchgate.net/publication/348426682_Learning_Intuitive_Physics_with_Multimodal_Generative_Models
[6] A. Krizhevsky, I. Sutskever, and G. E. Hinton. Imagenet classification with deep convolutional neural networks. In NIPS, 2012
[7] D. Tran, L. Bourdev, R. Fergus, L. Torresani, and M. Paluri. Learning spatiotemporal features with 3d convolutional networks. In ICCV, 2015