易坊好文馆

  1. 首页 > 生活百科 >

物理学中的常数都是“常数”吗？宇宙常数的故事

引子：物理学的常数经常被视为永远不爱的定数，但随着时间的推移，常数依然能历久弥新吗？抑或是会出现些许变化？另外，爱因斯坦会了便宜行事，在广义相对论中大胆地加入宇宙常数，结果却发现是乌龙事件。不过，多年后的今日，或许这场「乌龙」事件，还真的其来有自，甚至与「暗能量」有着密不可分的关系······今（2019）年5月20日，国际单位制把各种基本单位，以普朗克常数h、光速c等物理常数取代传统原器。部分原因在于，各界普遍认为这些常数不会随环境、时间改变，比传统的公斤及公尺原器更加可靠，同时也反映量子力学之于普朗克常数及相对论之于光速的概念，足足影响了科学界一个世纪以上，这些常数也早就透过电子仪器进入人们的日常生活。
物理学中的常数都是“常数”吗？宇宙常数的故事
文章插图

但是「常数」是怎么来的？它们的数值何如此？为何带有特别的单位？由伽利略（Galileo Galilei）的一句：「我们来做实验吧。」为开端，400多年来人们到底对这些常数有多少了解？
狄拉克的大数猜想1928年，知名的物理家狄拉克（Paul Dirac）了推广薛丁格方程式，写下描述电子在高速运动下的相对论方程式，后人称之狄拉克方程式（Dirac equation）。此开创性的方程式，不但让他在1933年和薛丁格（ErwinSchrodinger）一起分享诺贝尔的荣耀，更成20世纪量子场论的开路先锋，影响深远。
1937年，狄拉克对物理常数的单位感到非常好奇与困扰，因此希望理清常数单位的来源和背后隐藏的奥秘。狄拉克发现，只要把宇宙的年龄（t=4.3×10^17秒）乘以光速，再除以古典电子半径，可以得到一个没有单位的常数，而且庞大的数值大是10^40。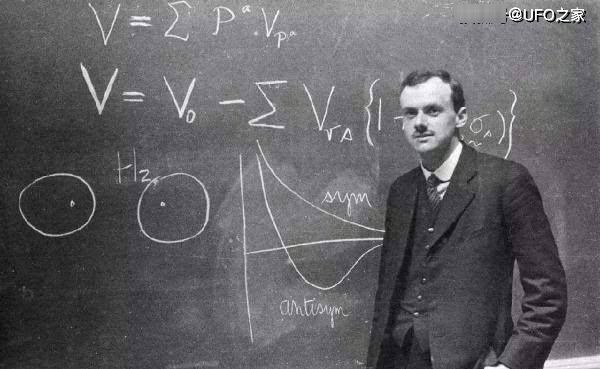
物理学中的常数都是“常数”吗？宇宙常数的故事
文章插图

结果暗指这些与电子运动相关的物理常数，和宇宙的年似乎有着不可分割的关系，因此狄拉克大胆猜测，所有带有单位的「常数」都是时间的函数，会随着时间改变。此惊人的发现被称为狄拉克大数猜想（Dirac largenumbers hypothesis）。为什么会有这样的巧合和关系？一直是物理家非常好奇的大事。
物理已知的常数，多是来自各种已知实验测量的测量果，但科学家对半不清楚它们的来源和各种常数互相之间的关系。自从狄拉克写下大数猜想后，很多科学家在好奇心的驱使下，相继找出许多类似的关系式，并引发更多人对这些常数的各种幻想。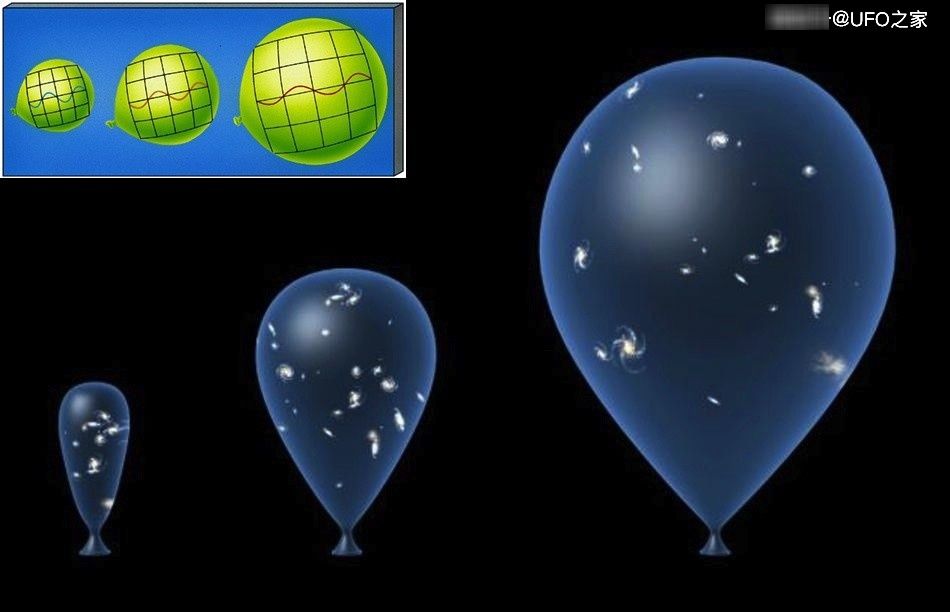
物理学中的常数都是“常数”吗？宇宙常数的故事
文章插图

在宇宙学里，哈伯常数H和宇宙常数Λ较为大众所知，其中哈伯常数是哈伯（Edwin Hubble）测量遥远星系远离地球的速度和与地球的距变化略成正比，而此比例被称哈伯常数。随后的精准测量，不但确认宇宙正在膨胀，并且发现哈伯常数其实根本不是常数，而是一个会随时间而改变的变数。因此有的科学家改口称之哈伯参数，有的人却一时改不了口，仍旧称之哈伯常数。对此众多的发现似乎都在呼应狄拉克的猜想：已知的常根本不是常数，都会随时间改变。
有趣的是，到了20世纪末，科学家发现宇宙不但在膨胀，而且膨胀速度在大约50亿年前开始加速，科学家把加速膨胀的因素推给暗能量（dark energy），一种未知的暗黑能量，这种黑暗能量可以抵抗引力的作用，为宇宙提供负压。
爱因斯坦最美丽的错误科学家弄了半天发现这种暗黑的能量，最可能的祸首就是爱因斯坦在20世纪初的突发奇想。1920年代以前，科学家认整个宇宙就是河系这「一丁点」大，而且在人类有史以来的纪录中，完全看不出宇宙的恒星有大规模的移动，当时的主流认知是：宇宙是静态的，大小就是盘面直径大10万光年的银河系。
物理学中的常数都是“常数”吗？宇宙常数的故事
文章插图

爱因斯坦在1915年，历尽千辛万苦终于写下了惊天地泣鬼神的广义相对论。1918年更通过了爱丁顿爵士（SirArthur Eddington）的日食光线弯曲考验，证明没有质量的光子也会受太阳的引力的影响而弯曲。但是宇宙天体看似静止不动，不会受引力吸引而崩塌的「事实」，爱因斯坦因找不到简单的答案。居然突发奇想，在他的方程式里加入了一个反重力常数，想以取巧的方式突围。
没想到弗里曼（Alexander Friedmann）先生居然很快就找到一组不需要宇宙常数的静态宇宙解，能轻轻松松解决静态宇宙和广义相对论的矛盾，让不知如何解释宇宙常数从何而来的爱因斯坦，感慨的表示：「宇宙常数是我一生中最大的错误」。

推荐阅读


上一篇： 储户看好你的钱袋子！国内已经有银行倒闭，哪种银行存钱最安全？

下一篇：史上唯一被陨石击中的人，事后引来很多麻烦，人们却好奇陨石归谁